Приклади розв’язування задач. Приклад 1. Електрон, початковою швидкістю якого можна знехтувати, пройшов прискорювальну різницю потенціалів U

Приклад 1. Електрон, початковою швидкістю якого можна знехтувати, пройшов прискорювальну різницю потенціалів U. Знайти довжину хвилі де Бройля для двох випадків: 1) U₁ = 51 B; 2) U₂ = 510 кВ.

Дано:

U₁ = 51 B

U₂ = 510 кВ = 5,1^.10 ⁵ В

____________________

– ?

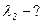
Розв’язування. Довжина хвилі де Бройля 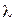для частинки залежить від її імпульсу р і визначається формулою

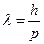, ( 1)

де h – постійна Планка.

Імпульс частинки можна визначити, якщо відома її кінетична енергія Е_к. Зв’язок імпульсу з кінетичною енергією різний для нерелятивістського випадку ( коли кінетична енергія частинки багато менша енергії її спокою ) і для релятивістського випадку (коли кінетична енергія збігається за величиною з енергією спокою частинки).

У нерелятивістському випадку

p= 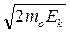, ( 2)

де m₀ – маса спокою частинки.

У релятивістському випадку

p= 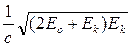, ( 3)

де Е₀ = m₀c² – енергія спокою частинки;

с – швидкість світла у вакуумі.

Формула (1) з урахуванням співвідношень (2) і (3) запишеться:

- у нерелятивістському випадку

, ( 4)

- у релятивістському випадку

. ( 5)

Зрівняємо кінетичні енергії електрона, який пройшов задані в умові задачі різниці потенціалів U₁ = 51 В и U₂ = 510 кВ, з енергією спокою електрона й, залежно від цього, вирішимо, яку з формул (4) або (5) варто застосувати для обчислення довжини хвилі де Бройля.

Як відомо, кінетична енергія електрона, який пройшов прискорювальну різницю потенціалів U, дорівнює

E_к = qU.

У першому випадку

Е_к = q₁U = 51 еB = 0,51^.10^-4 МeВ.

Отже, у цьому випадку можна застосувати формулу (4). Для спрощення розрахунків помітимо, що Е_к = 10^-4 m_oc². Підставивши цей вираз у формулу (4), перепишемо її у вигляді

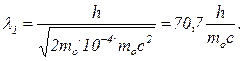
Урахувавши, що є комптонівська довжина хвилі 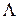, одержимо

.

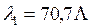Оскільки 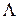=2,43 пм, то

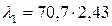пм = 171 пм.

У другому випадку кінетична енергія

E_к = qU₂ = 510 кеВ = 0,51 МеВ,

тобто дорівнює енергії спокою електрона. У цьому випадку необхідно застосувати релятивістську формулу (5). Урахувавши, що Е_к = 0,51МэВ = = m_oc², за формулою (5) знайдемо

,

Підставивши значення й виконавши необхідні розрахунки, одержимо

1,40 пм.

Приклад 2. Кінетична енергія електрона в атомі водню не перевищує величину 10еВ. Використовуючи співвідношення невизначеностей, оцінити мінімальні розміри атома.

Дано:

Е_к = 10 еВ

_________

l_min – ?

Розв’язування. Співвідношення невизначеностей для координати й імпульсу записують так:

/2,

де – невизначеність імпульсу частинки (електрона);

– невизначеність координати частинки (у цьому випадку електрона);

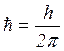– постійна Планка (h поділена на 2 ).

Із співвідношення невизначеностей випливає, що чим точніше визначається положення частинки в просторі, тим більше невизначеним стає імпульс, а отже, і енергія частинки. Нехай атом має лінійні розміри l, тоді електрон атома буде перебувати десь у межах області з невизначеністю

.

В цьому випадку співвідношення невизначеностей можна записати у вигляді

,

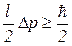звідки

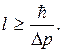
Фізично розумна невизначеність імпульсу 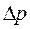не повинна перевищувати значення самого імпульсу p, тобто .

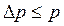Імпульс р пов'язаний з кінетичною енергією Е_к співвідношенням

р = .

Замінимо 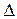р значенням (така заміна не збільшить 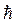). Перейдемо до рівності

l_min = .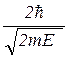

Підставивши числові значення й виконавши обчислення, одержимо

l_min = м = 1,16^.10^{-10 м = 116 пм.}

Приклад 3. Хвильова функція описує основний стан частинки в нескінченно глибокому прямокутному ящику шириною l. Обчислити імовірність знаходження частинки в малому інтервалі 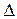l = 0,01l у двох випадках: 1) поблизу стінки ( 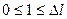); 2) у середній частині ящика .

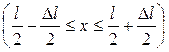Дано:

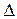l = 0,01l

__________

W₁ – ?

W₂ – ?

Розв’язування. Імовірність того, що частинка буде виявлена в інтервалі dx (від х до х+dх), пропорційна цьому інтервалу й квадрату модуля хвильової функції, яка описує даний стан

dW =

У першому випадку шукана імовірність знаходиться інтегруванням у межах від 0 до 0,01l

W = ( 1)

Знак модуля пропущений, тому що - функція в цьому випадку не є комплексною.

Оскільки х змінюється в інтервалі ( 0 0,01l ) і, отже, <<1, справедлива наближена рівність

.

З урахуванням цього вираз (1) набуде вигляду

W = .

Після інтегрування одержимо

W = .

У другому випадку можна обійтися без інтегрування, оскільки квадрат модуля хвильової функції поблизу її максимуму в заданому малому інтервалі ( l = 0,01l) практично не змінюється. Шукана імовірність у другому випадку визначається виразом

W =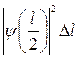

або

W = .

Задачі

623. Знайти: а) радіуси трьох перших борівських електронних рівнів в атомі водню; б) швидкість електрона на цих рівнях.

Відповідь: = 53 пм; = 212 пм; 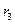= 477 пм; 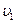= 2,19 Мм/c; = 1,1 Мм/c; 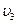= 0,73 Мм/c.

624. Знайти числове значення кінетичної, потенціальної і повної енергій електрона на першому борівському енергетичному рівні.

Відповідь: 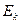= 13,6 еВ; U = -27,2 еВ; E = -13,6 еВ.

625. Обчислити кінетичну енергію електрона, який перебуває на n-му енергетичному рівні атома водню. Задачу розв’язати для n = 1, 2, 3 і ∞.

Відповідь: ; ; ; ; .

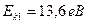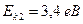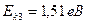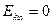626. Знайти: а) період обертання електрона на першому борівському енергетичному рівні в атомі водню; б) кутову швидкість обертання електрона.

Відповідь: 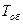= 1,52^.10 с; ω = 4,13^.10 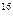рад/c.

627. Знайти: а) радіус першого борівського енергетичного рівня для одноразово іонізованого атома гелію; б) швидкість електрона на цьому рівні.

Відповідь: = 26,6 пм; 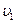= 4,38 Мм/c.

628. Скориставшись постулатами теорії Бора, обчислити: а) радіуси двох перших енергетичних рівнів в атомі водню; б) швидкості електрона на цих рівнях.

Відповідь: = 53 пм; = 212 пм; 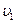= 2,19 Мм/c; = 1,1 Мм/c.

629. На якому енергетичному рівні в атомі водню швидкість електрона дорівнює 734 км/с?

Відповідь: n = 3.

630. Визначити кутову швидкість електрона на першому борівському енергетичному рівні в атомі водню.

Відповідь: ω = 4,13 10 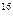с .

631. Розрахувати значення кулонівської сили притягання і напруженість електричного поля ядра на першому й другому енергетичних рівнях в атомі водню.

Відповідь: 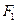= 82,4 нН; 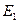= 512 ГВ/м; 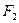= 5,14 нН; 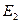= 32,1 ГВ/м.

632. Атом водню переводиться з нормального стану в збуджений, що характеризується головним квантовим числом 2. Розрахувати енергію збудження цього атома.

Відповідь: 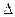E = 10,2 еВ.

633. Атом водню перебуває в основному стані. У скільки разів збільшиться радіус енергетичного рівня електрона в атомі, якщо він поглине квант з енергією 12,09 еВ?

Відповідь: / = 9.

634. Перехід електрона в атомі водню з n-го на k-й енергетичний рівень (k = 1) супроводжується випромінюванням фотона з довжиною хвилі 102,6 нм. Знайти радіус n-го енергетичного рівня.

Відповідь: r = 475 пм.

635. Показати, що для атома водню на борівських стаціонарних енергетичних рівнях укладається ціле число довжин хвиль де Бройля. Визначити довжини хвиль де Бройля на першому і третьому енергетичних рівнях.

Відповідь: 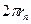= nλ; = 332 пм; 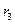= 996 пм.

636. Яку роботу необхідно виконати, щоб перевести електрон з другого енергетичного рівня атома водню за межі його притягання ядром?

Відповідь: A = 5,45^.10^-19 Дж.

637. Скориставшись постулатами Бора, визначити для електрона, що перебуває на першому й другому енергетичних рівнях в атомі водню, відношення радіусів цих рівнів.

Відповідь: / = 4.

638. Скориставшись постулатами Бора, визначити для електрона, що перебуває на першому й другому енергетичних рівнях в атомі водню, відношення магнітного моменту електрона до його механічного моменту.

Відповідь: Кл / кг.

639. Скориставшись постулатами Бора, визначити для електрона, що перебуває на першому й другому енергетичних рівнях в атомі водню, відношення їх повних енергій.

Відповідь: .

640. Визначити, як зміниться орбітальний момент імпульсу електрона в атомі водню при його переході із збудженого стану в основний стан, якщо при цьому випромінюється один квант енергії з довжиною хвилі λ = 97,25 нм.

Відповідь: Зменшиться у 4 рази.

641. У спектрі атомарного водню інтервал між першими двома спектральними лініями, які належать до серії Бальмера, складає λ = 6,54^.10 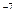м. Визначити сталу Рідберга.

Відповідь: R = 1,09 10 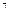м .

642. Квант світла з енергією Е = 15 еВ вибиває електрон з атома водню, що перебуває в нормальному стані. З якою відносною швидкістю буде рухатися цей електрон далеко від ядра?

Відповідь: υ = 7,01^.10 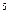м/c.

643. Обчислити циклічну частоту обертання електрона на другому борівському енергетичному рівні іона Не .

Відповідь: ω = 2,07^.10 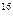c .

644. Знайти для воднеподібних систем магнітний момент, що відповідає руху електрона на n-му енергетичному рівні, а також відношення магнітного моменту до механічного.

Відповідь:

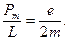
645. Обчислити індукцію магнітного поля в центрі атома водню, обумовленого рухом електрона по першому борівському енергетичному рівні.

Відповідь: B = 12,5 Тл.

646. Енергія зв'язку електрона в основному стані атома Не дорівнює = 24,6 еВ. Знайти енергію, необхідну для видалення обох електронів з цього атома.

Відповідь: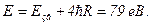

647. Обчислити за теорією Бора період обертання електрона в атомі водню, що перебуває в збудженому стані з головним квантовим числом n = 2.

Відповідь: 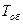= 1,22^.10 с.

648. У скільки разів зміниться період 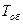обертання електрона в атомі водню, якщо при переході в незбуджений стан атом випромінює фотон з довжиною хвилі λ = 97,5 нм?

Відповідь: .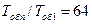

649. На скільки змінилася кінетична енергія електрона в атомі водню при випромінюванні ним фотона з довжиною хвилі λ = 435нм?

Відповідь: .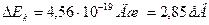

650. Знайти найбільшу довжину хвилі у видимій області спектра атома водню.

Відповідь: λ = 656 нм.

651. Знайти найбільшу довжину хвилі в ультрафіолетовій серії Лаймана спектра атома водню. Яку найменшу швидкість повинні мати електрони, щоб під час збудження атомів водню ударами електронів з‘явилася ця лінія?

Відповідь: λ = 121 нм; υ = 1,9 Мм/с.

652. Визначити потенціал іонізації атома водню.

Відповідь: 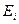= 13,6 В.

653. Визначити перший потенціал збудження атома водню.

Відповідь: 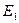= 10,2 В.

654. Яку найменшу енергію (в електрон-вольтах) повинні мати електрони, щоб при збудженні атомів водню ударами цих електронів появилися всі лінії всіх серій спектра водню? Яку найменшу швидкість повинні мати ці електрони?

Відповідь: E = 13,6 еВ; υ = 2,2 Мм/с.

655. У яких межах повинна змінюватись енергія електронів, щоб при збудженні ними атомів водню, які перебувають у нормальному стані, енергетичний спектр випромінювання мав тільки одну спектральну лінію?

Відповідь: 10,2 еВ ≤ Е ≤ 12,1 еВ.

656. Яку найменшу енергію (в електрон-вольтах) повинні мати електрони, щоб при збудженні ними атомів водню, спектр водню мав три спектральні лінії? Знайти довжини хвиль цих ліній.

Відповідь: E ≥ 12,04 еВ; 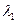= 656 нм; 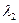= 122 нм; = 103 нм.

657. У яких межах повинні розміщуватись довжини хвиль монохроматичного світла, щоб при збудженні атомів водню квантами цього світла спостерігалися три спектральні лінії?

Відповідь: 97,3 нм ≤ λ ≤ 102,6 нм.

658. На скільки зміниться кінетична енергія електрона в атомі водню при випромінюванні ним фотона з довжиною хвилі λ = 486 нм?

Відповідь: ΔE 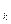= 2,56 еВ.

659. У яких межах повинні лежати довжини хвиль монохроматичного світла, щоб при збудженні атомів водню квантами цього світла радіус енергетичного рівня електрона збільшився в 9 разів?

Відповідь: 97,3 нм ≤ λ ≤ 102,6 нм.

660. На дифракційну гратку нормально падає пучок світла від розрядної трубки, наповненої атомарним воднем. Стала гратки дорівнює 5^.10^{-4 см}. Якому переходу електрона відповідає спектральна лінія, що спостерігається за допомогою цієї гратки у спектрі п'ятого порядку під кутом 41°?

Відповідь: 3 →2.

661. Знайти найменшу довжину хвилі фотона, що випромінюється електроном при переході із збудженого в основний стан в іоні гелію .

Відповідь: λ = 30,4 нм.

662. Яка найменша енергія необхідна для збудження іона ?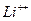

Відповідь: E = 92 еВ.

663. Знайти різницю енергій іонізації іонів та атома водню.

Відповідь: ΔE = 41 еВ.

664. Визначити межу серії водневих ліній, розміщених в далекій ультрафіолетовій частині спектра (серія Лаймана).

Відповідь: λ = (121,6 –91,2) нм.

665. Визначити енергію фотона, що відповідає найменшій довжині хвилі в ультрафіолетовій серії водню.

Відповідь: E = 2,18^.10 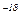Дж.

666. Знайти довжини хвиль першої, другої і третьої ліній видимої серії водню (серія Бальмера).

Відповідь: 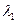= 656,3 нм; 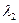= 486,1 нм; = 434 нм.

667. Чому дорівнює довжина хвилі четвертої спектральної лінії в інфрачервоній області спектра водню (серія Пашена)?

Відповідь: 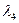= 1,005 мкм.

668. Експериментально встановлено, що друга спектральна лінія водневої серії Брекета відповідає довжині хвилі 2,63 мкм. На підставі цих даних установити наближене значення сталої Рідберга.

Відповідь: R =1,095^.10 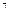м .

669. Найбільша довжина хвилі спектральної водневої лінії серії Лаймана 121,6 нм. Обчислити найбільшу довжину хвилі в серії Бальмера.

Відповідь: λ = 656,6 нм.

670. При переході електрона атома водню з одного з можливих енергетичних рівнів на інший, більш близький до ядра, енергія атома зменшується на 1,892 еВ. Визначити довжину хвилі випромінювання.

Відповідь: λ = 657 нм.

671. Обчислити найменше значення енергії, при якому в результаті збудження атомів водню з'являється повний спектр.

Відповідь: E = 13,63 еВ.

672. Атомарний водень переведений з нормального стану в збуджений з головним квантовим числом n = 3. Які спектральні лінії можуть з'явитися в спектрі водню при переході атома зі збудженого стану в нормальний?

Відповідь: 2→1, λ =121,6 нм; 3→1, λ =102,6 нм; 3→2, λ = 656,3 нм .

673. Які спектральні лінії з'являться у видимій області спектра при збудженні атомів водню електронами з енергією 13 еВ?

Відповідь: 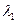= 656,3 нм; 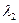= 486,1 нм; = 434,0 нм.

674. Атоми водню освітлюється ультрафіолетовим випромінюванням з довжиною хвилі 100 нм. Визначити, які спектральні лінії з'являться в спектрі водню.

Відповідь: 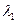= 121,6 нм; 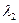= 102,6 нм; = 656,6 нм.

675. Різниця довжини хвиль між головними лініями серій Лаймана і Бальмера в спектрі атомарного водню дорівнює λ = 534,7 нм. Визначити за цими даними сталу Планка.

Відповідь: h = 6,64 ^.10 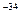Дж с.

676. Електрон, що перебуває далеко від ядра атома водню і має швидкість υ = 1,870^.10 м/с, захоплюється цим ядром, у результаті чого утворюється збуджений атом водню. Визначити довжину хвилі фотона, що випромінюється при переході атома в нормальний стан.

Відповідь: λ = 121 нм.

677. Які спектральні лінії з'являться при збудженні атомарного водню електронами з енергією: а) 12,5 еВ; б) 14 еВ?

Відповідь: а) 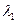= 103 нм; 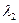= 127 нм; = 656 нм; б) всі.

678. При спостереженні спектра атомарного водню, отриманого за допомогою дифракційної гратки з періодом d = 2 мкм, виявлено, що одна зі спектральних ліній серії Бальмера в спектрі другого порядку відповідає куту дифракції 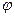=29°05''. Визначити головне квантове число енергетичного рівня атома, переходу з якого відповідає дана лінія.

Відповідь: n = 4.

679. Скориставшись постулатами Бора, визначити для дворазово іонізованого атома літію (Li ) радіус першого енергетичного рівня.

Відповідь: = 18 пм.

680. Визначити довжини хвиль де Бройля електрона й протона, які пройшли однакову прискорювальну різницю потенціалів U = 400 В.

Відповідь: 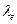= 61,4 пм; 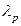=1,43 пм.

681. Електрон, початковою швидкістю якого можна знехтувати, пройшов прискорювану різницю потенціалів U. Знайти довжину хвилі де Бройля для двох випадків: а) U = 51 B, б) U = 510 кВ.

Відповідь: λ₁ =172 пм; λ₂ = 1,4 пм.

682. Яку прискорювану різницю потенціалів має пройти електрон, щоб довжина хвилі де Бройля дорівнювала 10^{-8 м?}

Відповідь: U₁ = 0,015 В.

683. Порівняти довжину хвилі де Бройля для електрона і частинки масою 0,1 г, які рухаються з однаковими швидкостями. Який висновок можна зробити?

Відповідь: λ_е/λ_ч = 1,09^.10²⁶ разів.

684. Визначити довжину хвилі де Бройля для протона, що рухається зі швидкістю 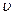= 0,6 с (с – швидкість світла у вакуумі).

Відповідь: λ = 1,76^.10^{-15 м.}

685. Електрон рухається вздовж колової траєкторії радіусом 0,5 см в однорідному магнетному полі з індукцією 8 мТл. Визначити довжину хвилі де Бройля електрона.

Відповідь: λ =1,035^.10 ^-10 м.

686. Визначити довжину хвилі де Бройля електрона, якщо його кінетична енергія дорівнює 1 еВ.

Відповідь: λ = 10^{-9 м.}

687. Визначити довжину хвилі де Бройля і кінетичну енергію протона, який рухається зі швидкістю 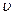= 0,99 с (с – швидкість світла у вакуумі).

Відповідь: λ = 188^.10^{-16 м; Т= 9,15.}10^-10 Дж.

688. Порівняти довжини хвиль де Бройля електрона й іона He⁺ , які пройшли однакову різницю потенціалів U = 1 кВ.

Відповідь: λ_е =3,88^.10^{-11 м}; λ_п = 4,53^.10^{-13 м.}

689. З якою швидкістю рухається електрон, якщо довжина хвилі де Бройля електрона дорівнює 2,456 нм?

Відповідь: υ =2,96^.10⁵м/с.

690. Знайдіть довжину хвилі де Бройля для протона, який пройшов прискорюючи різницю потенціалів: 1) 1 кВ, 2) 1 МВ.

Відповідь: λ₁ = 9,06^.10^{-13 м}; λ₂ = 2,87^.10^{-14 м.}

691. Кінетична енергія протона дорівнює його енергії спокою. Обчислити довжину хвилі де Бройля цього протона.

Відповідь: =7,64.10^{-16 м.}

692. Визначити кінетичні енергії протона і електрона, для яких довжина хвилі де Бройля дорівнює 0,06 нм.

Відповідь: 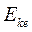= 419 еВ; 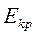= 0,228 еВ.

693. Протон має кінетичну енергію, що дорівнює його енергії спокою. У скільки разів зміниться довжина хвилі де Бройля протона, якщо його кінетична енергія збільшиться у 2 рази?

Відповідь: / 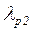=1,63.

694. Кінетична енергія електрона дорівнює його енергії спокою. Обчислити довжину хвилі де Бройля для такого електрона.

Відповідь: = 1,4 пм.

695. Використовуючи постулати Бора, знайти зв'язок між довжиною хвилі де Бройля і довжиною колового енергетичного рівня.

Відповідь: .

696. Яку кінетичну енергію повинен мати електрон, щоб його довжина хвилі де Бройля дорівнювала комптонівській довжині хвилі?

Відповідь: = 0,25 МеВ.

697. Який імпульс повинен мати протон, щоб його хвиля де Бройля дорівнювала комптонівській довжині хвилі?

Відповідь: p = 5⋅10 кг⋅м/c.

698. Знайти довжину хвилі де Бройля для електрона, що перебуває в русі на першому борівському енергетичному рівні в атомі водню.

Відповідь: = 0,33 нм.

699. Написати вираз для хвилі де Бройля λ релятивістської частинки маси m; а) через її швидкість υ; б) через кінетичну енергію .

Відповідь:

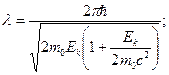
700. При якому значенні швидкості υ довжина хвилі де Бройля мікрочастинки дорівнює її комптонівській довжині хвилі?

Відповідь: υ = 0,71 с.

701. При якій швидкості υ електрона його довжина хвилі де Бройля буде дорівнювати 500 нм?

Відповідь: 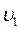=1,46 км/с.

702. Знайти довжину хвилі де Бройля електрона, що рухається зі швидкістю 20 км/с. До якої області електромагнетного спектра можна віднести довжину хвилі, яка дорівнює знайденій?

Відповідь: = 36,4 нм.

703. Швидкості теплових нейтронів ядерних реакторів близькі до 2,5 км/с. Знайти довжину хвилі де Бройля для таких нейтронів.

Відповідь: = 159 пм.

704. У телевізійній трубці проекційного типу електрони розганяються до швидкості 10⁸ м/с. Визначити довжину хвилі де Бройля електронів без урахування залежності маси від швидкості.

Відповідь: = 7,27 пм.

705. Знайти довжину хвилі де Бройля для електрона, що рухається зі швидкістю, яка дорівнює 0,8 швидкості світла. Врахувати зміну маси зі швидкістю.

Відповідь: = 1,82 пм.

706. Обчислити довжину хвилі де Бройля для протона з кінетичною енергією 100 еВ.

Відповідь: 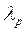= 2,86 пм.

707. Знайти довжину хвилі де Бройля для α-частинки, нейтрона і молекули азоту, що рухаються із середньою квадратичною швидкістю при температурі 25° С.

Відповідь: = 73 пм; 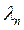= 145 пм; 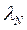= 28 пм.

708. Електрон рухається на другому енергетичному рівні атома водню. Знайти його довжину хвилі де Бройля.

Відповідь: = 0,665 нм.

709. Електрон має кінетичну енергію = 1,02 МеВ. У скільки разів зміниться довжина хвилі де Бройля, якщо кінетична енергія електронів зменшиться удвічі.

Відповідь: 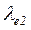/ 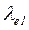= 1,63.

710. Середня кінетична енергія електрона в основному стані атома водню дорівнює 13,6еВ. Використовуючи співвідношення невизначеностей, знайти найменшу похибку, з якою можна обчислити координату електрона в атомі.

Відповідь: Δx = 52,8 пм.

711. Показати, що для частинки, невизначеність координати якої складає Δх = λ/(2π) (λ – довжина хвилі де Бройля), невизначеність її швидкості за величиною дорівнює самій швидкості частинки.

712. Виходячи зі співвідношення невизначеностей, оцінити розміри ядра атома, вважаючи, що мінімальна енергія нуклона в ядрі 8 МеВ.

Відповідь: d = 1,6 фм.

713. Використовуючи співвідношення невизначеностей, оцінити енергію електрона, що перебуває на першому борівському енергетичному рівні в атомі водню.

Відповідь: E = 13,6 еВ.

714. Електрон перебуває в одновимірній потенціальній ямі з нескінченно високими стінками, ширина якої 1,4 10 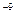м. Визначити енергію, що випромінюється при переході електрона з третього енергетичного рівня на другий.

Відповідь: E = 1,52 ^.10 Дж = 0,95 еВ.

715. Електрон знаходиться в одновимірній потенціальній ямі з нескінченно високими стінками, ширина якої l = 1 нм. Визначити найменшу різницю енергетичних рівнів електрона.

Відповідь: ΔE = 1,78 ^.10 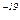Дж = 1,11 еВ.

716. Частинка в потенціальній ямі шириною l перебуває у збудженому стані. Визначити імовірність перебування частинки в інтервалі 0 < x < на другому енергетичному рівні.

Відповідь: W = .

717. Визначити ширину одновимірної потенціальної ями з нескінченно високими стінками, якщо при переході електрона з третього енергетичного рівня на другий випромінюється енергія 1 еВ?

Відповідь: l = 1,37 нм.

718. Знайти хвильову функцію і значення енергії частинки масою m, що перебуває в одновимірній нескінченно глибокій потенціальній ямі шириною l .

Відповідь: .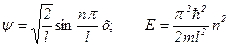

719. Альфа-частинка знаходиться у нескінченно глибокій одновимірній потенціальній ямі. Чому дорівнює ширина ями, якщо мінімальна енергія частинки складає 6 МеВ?

Відповідь: l = 2,9^.10^{-15 м.}

720. Електрон знаходиться у нескінченно глибокій одновимірній потенціальній ямі шириною 0,1 нм. Обчислити довжину хвилі випромінювання при переході електрона з другого на перший енергетичний рівень.

Відповідь: λ = 11 нм.

721. Протон знаходиться в нескінченно глибокій одновимірній потенціальній ямі шириною 0,01 пм. Обчислити довжину хвилі випромінювання при переході протона з третього на другий енергетичний рівень.

Відповідь: λ = 1,22^.10^{-13 м.}

722. Атом водню знаходиться у нескінченно глибокій одновимірній потенціальній ямі шириною 0,1 нм. Обчислити різницю енергій сусідніх рівнів, які відповідають середній енергії теплового руху атома при температурі 625 К.

Відповідь: 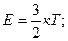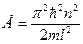; n = 2;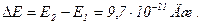

723. Частинка знаходиться у нескінченно глибокій одновимірній потенціальній ямі шириною l в основному стані. У яких точках ями густина імовірності виявлення частинки збігається з класичною густиною імовірності.

Відповідь: ω_кл.= ω =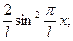

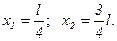
724. Частинка знаходиться у нескінченно глибокій одновимірній потенціальній ямі шириною l в основному стані. Чому дорівнює відношення густин імовірності виявлення частинки в центрі ями до класичної густини імовірності.

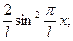Відповідь: ω_кл.= ω = x =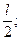

725. Частинка знаходиться у нескінченно глибокій одновимірній потенціальній ямі шириною l на першому збудженому рівні. У яких точках ями густина імовірності виявлення частинки максимальна?

Відповідь: ω = n=2;

726. Частинка знаходиться у нескінченно глибокій одновимірній потенціальній ямі шириною l на другому енергетичному рівні. Визначити імовірність виявлення частинки в межах від 0 до l/3.

Відповідь: W=0,40.

727. Частинка знаходиться у нескінченно глибокій одновимірній потенційній ямі шириною l в основному стані. Знайти відношення імовірності перебування частинки в межах від 0 до l/3 і від l/3 до 2l/3.

Відповідь:

728. Частинка знаходиться у нескінченно глибокій одновимірній потенціальній ямі шириною l. Обчислити відношення імовірності перебування частинки в межах від 0 до l/4 для першого і другого енергетичних рівнів.

Відповідь: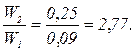

729. Частинка перебуває в основному стані в одновимірній прямокутній потенціальній ямі шириною l з абсолютно непроникними стінками (0<x<l ). Знайти ймовірність перебування частинки в області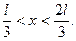

Відповідь: .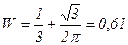

730. Електрон перебуває в прямокутній потенціальній ямі з непроникними стінками. Ширина ями l = 0,2 нм, енергія електрона в ямі E = 37,8 еВ. Визначити номер n енергетичного рівня.

Відповідь: n = 2.

731. Частинка перебуває в потенціальній ямі в основному стані. Яка імовірність виявлення частинки: а) у середній третині ями; б) у крайній третині ями?

Відповідь: 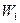= 0,609; = 0,195.

732. Частинка перебуває у нескінченно глибокій, одновимірній, прямокутній потенціальній ямі. Знайти відношення різниці енергій сусідніх енергетичних рівнів до енергії 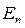частинки у випадку, якщо n = 2.

Відповідь: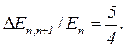

733. Електрон перебуває у нескінченно глибокій, одновимірній, прямокутній потенціальній ямі шириною l = 0,1 нм. Визначити в електрон-вольтах найменшу різницю енергетичних рівнів електрона.

Відповідь: ΔЕ = 112 еВ.

734. Частинка в нескінченно глибокій, одновимірній, прямокутній потенціальній ямі шириною l перебуває у збудженому стані (n = 3). Визначити, у яких точках інтервалу 0 < х < l густина імовірності перебування частинки має максимальне і мінімальне значення.

Відповідь:

735. У прямокутній потенціальній ямі шириною l з абсолютно непроникними стінками (0 < х < l) перебуває частинка в основному стані. Знайти імовірність W знаходження цієї частинки в області l/4 < x< l.

Відповідь: W = 0,82.

736. Частинка в нескінченно глибокій, одновимірній, прямокутній потенціальній ямі перебуває в основному стані. Яка ймовірність W виявлення частинки в крайній чверті ями?

Відповідь: W = 0,09.

737. Частинка перебуває в основному стані в прямокутній ямі шириною l з абсолютно непроникними стінками. У скільки разів відрізняються імовірності виявити частинки: a) у крайній третині ями; б) у крайній чверті ями?

Відповідь: 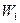/ = 2,17.

738. Моноенергетичний потік електронів (Е = 100 еВ) падає на низький прямокутний потенціальний бар’єр нескінченної ширини. Визначити висоту потенціального бар’єра U, якщо відомо, що 4% електронів, що падають на бар’єр, відбиваються.

Відповідь: U = 55,6 еВ.

739. Електрон з енергією Е = 4,9 еВ рухається у позитивному напрямку осі x (рис.1). Висота U потенціального бар’єра дорівнює 5 еВ. При якій ширині d бар’єра ймовірність проходження електрона крізь нього буде дорівнювати 0,2.

Відповідь: d = 0,495 нм.

Рисунок 1

740. Написати рівняння Шредінгера для електрона з енергією Е, що рухається в позитивному напрямку осі x для областей I та II (рис.1), якщо на межі цих областей існує низький потенціальний бар’єр висотою U.

Відповідь: .

741. На шляху електрона з довжиною хвилі де Бройля 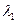= 0,1 нм розміщений потенціальний бар’єр висотою U = 120 еВ. Визначити довжину хвилі де Бройля 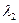після проходження бар’єра.

Відповідь: .

742. Електрон з енергією Е = 100 еВ попадає на потенціальний бар'єр висотою U = 64 еВ. Визначити імовірність W того, що електрон відіб'ється від бар'єра.

Відповідь: W = 0,0625.

743. Визначити показник заломлення n хвиль де Бройля при проходженні частинкою потенціального бар'єра c коефіцієнтом відбиття ρ = 0,5.

Відповідь: n = 0,172.

744. При якому відношенні висоти U потенціального бар'єра і енергії Е електрона, що падає на бар'єр, коефіцієнт відбиття ρ = 0,5?

Відповідь: = 0,971.

745. Кінетична енергія електрона в два рази перевищує висоту U потенціального бар'єра. Визначити коефіцієнт відбиття ρ і коефіцієнт проходження τ електронів на межі бар'єра.

Відповідь: ρ = 0,0295; τ = 0,97.

746. Коефіцієнт проходження протонів τ через потенціальний бар'єр дорівнює 0,8. Визначити показник заломлення хвиль де Бройля на межі бар'єра.

Відповідь: = 0,384.

747. Обчислити коефіцієнт проходження τ електрона з енергією Е = 100 еВ через потенціальний бар'єр висотою U = 99,75 еВ.

Відповідь: τ = 0,2.

748. Ширина d прямокутного потенціального бар'єра дорівнює 0,2 нм. Різниця енергій U - Е = 1 еВ. У скільки разів зміниться імовірність W проходження електрона через бар'єр, якщо різниця енергій зросте в n = 10 разів?

Відповідь: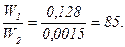

749. Електрон з енергією E = 9 еВ рухається у позитивному напрямку осі x. При якій ширині d потенціального бар'єра коефіцієнт прозорості D = 0,1, якщо висота U бар'єра дорівнює 10 еВ? Зобразити на рисунку вигляд хвильової функції (її дійсну частину) у межах кожної з областей I, II, III (див. рис.1).

Відповідь: нм.

750. При якій ширині d прямокутного потенціального бар'єра коефіцієнт прозорості D для електронів дорівнює 0,01? Різниця енергій U - Е = 10 еВ.

Відповідь: d = 0,143 нм.

751. Електрон з енергією Е рухається у позитивному напрямку осі х. При якому значенні U - Е, вираженому в електрон-вольтах, коефіцієнт прозорості D = 10 , якщо ширина d бар'єра дорівнює 0,1 нм?

Відповідь: еВ.

752. Електрон з енергією E = 9 еВ рухається у позитивному напрямку осі x. Оцінити імовірність W того, що електрон пройде через потенціальний бар'єр, якщо його висота U = 10 еВ і ширина d = 0,1 нм.

Відповідь: W = 0,357.

753. Прямокутний потенціальний бар'єр має ширину d = 0,1 нм. При якій різниці енергій U - Е ймовірність W проходження електрона через бар'єр дорівнює 0,99?

Відповідь: U - Е = 0,95^.10 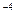еВ.

754. Ядро випромінює α-частинки з енергією E =5 МеВ. У першому наближенні можна вважати, що α-частинки проходять через прямокутний потенціальний бар'єр висотою U = 10 МеВ і шириною d = 5 фм. Знайти коефіцієнт прозорості D бар'єра для α-частинок.

Відповідь: D = 0,53^.10^-4.

755. Протон і електрон пройшли однакову прискорювальну різницю потенціалів U = 10 кВ. У скільки разів відрізняються коефіцієнти прозорості для електрона і для протона, якщо висота U бар'єра дорівнює 20 кеВ і ширина d = 0,1 пм?

Відповідь: .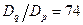

756. Електрон має енергію Е = 10 еВ. Визначити, у скільки разів зміняться його швидкість υ, довжина хвилі де Бройля λ і фазова швидкість υ_ф при проходженні через потенціальний бар'єр (див. рис.1) висотою U = 6 еВ.

Відповідь: 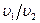= 0,632; = 1,58; 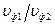= 0,632.

757. Коефіцієнт відбиття протона від потенціального бар'єра ρ дорівнює 2,5^.10 . Визначити, який відсоток складає висота U бар'єра від кінетичної енергії протонів, що падають на бар'єр.

Відповідь: = 2%.

758. Електрон з енергією Е = 10 еВ падає на потенціальний бар'єр. Визначити висоту U бар'єра, при якій показник заломлення n хвиль де Бройля і коефіцієнт відбиття ρ чисельно збігаються.

Відповідь: U = 9,13 еВ.

759. Псі-функція деякої частинки має вигляд 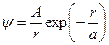, де r – відстань частинки від силового центра; А – константа. Знайти: а) значення коефіцієнта А; б) середню відстань r частинки від центра.

Відповідь: .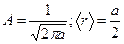

760. Псі-функція деякої частинки має вигляд 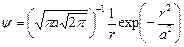, де r – відстань частинки від силового центра; а – константа. Знайти середню відстань частинки від центра.

Відповідь: .

761. Хвильова функція, що описує рух електрона в основному стані атома водню, має вигляд 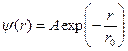, де А – деяка стала; 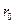– перший борівський радіус. Середнє значення потенціальної енергії для цього стану дорівнює . Знайти значення сталої А.

Відповідь: .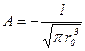

762. Написати рівняння Шредінгера для електрона, що перебуває у воднеподібному атомі.

Відповідь: .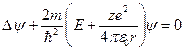

763. Написати рівняння Шредінгера для лінійного гармонічного осцилятора. Врахувати, що сила, яка повертає частинку до положення рівноваги, F = kх (де k – коефіцієнт пропорційності; х – зміщення).

Відповідь: .

764. Провести нормування хвильової функції .

Відповідь: .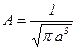

765. Чим обумовлена вимога скінченності ψ-функції?

766. Рівняння Шредінгера для стаціонарних станів має вигляд . Обґрунтувати, виходячи з цього рівняння, вимоги, що висувають до хвильової функції, її неперервність і неперервність першої похідної від хвильової функції.

767. Електрон у атомі водню описується у основному стані хвильовою функцією 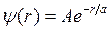. Визначити відношення імовірностей 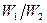перебування електрона у сферичних шарах товщиною Δr = 0,01a та радіусами = 0,5 а і = 1,5 а.

Відповідь: .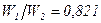

768. Визначити короткохвильову межу суцільного спектра рентгенівського випромінювання, якщо рентгенівська трубка працює під напругою U =30 кВ.

Відповідь: = 41 пм.

769. Обчислити найбільшу довжину хвилі у К-серії характеристичного рентгенівського спектра скандію (z=21).

Відповідь: = 304 пм.

770. Під час дослідження лінійчатого рентгенівського спектра деякого елементу було знайдено, що довжина хвилі λ лінії дорівнює 76 пм. Що це за елемент?

Відповідь: Z = 41; ніобій.

771. Яку найменшу різницю потенціалів необхідно прикласти до рентгенівської трубки, антикатод якої покритий ванадієм (Z = 23), щоб у спектрі рентгенівського випромінювання з’явились усі лінії К-серії ванадію? Межа К-серії ванадію λ=226 пм.

Відповідь: = 5,5 кВ.

772. Визначити енергію E фотона, який відповідає K_α-лінії у характеристичному спектрі марганцю (Z = 25).

Відповідь: E =5,9 кеВ.