Тема 18 Электромагнитные колебания

1. В контуре, состоящем из конденсатора емкости С и катушки индуктивности L, совершаются свободные незатухающие колебания, при которых амплитуда напряжения на конденсаторе равна U_m . Найти связь между током I в контуре и напряжением U на конденсаторе.

2. Колебательный контур состоит из конденсатора емкости С, катушки индуктивности L с пренебрежимо малым сопротивлением и ключа. При разомкнутом ключе конденсатор разряжается до напряжения U_m ,и затем в момент t=0 замкнули ключ. Найти: а) ток в контуре как функцию времени; б) ЭДС самоиндукции в катушке в моменты, когда электрическая энергия конденсатора равна энергии тока в катушке.

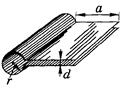
3. Найти собственную частоту ω₀ резонатора, считая что его плоская часть является конденсатором, а цилиндрическая – индуктивностью. Необходимые размеры указаны на рисунке.

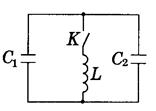
4. В колебательном контуре индуктивность катушки L=2,5 мГн, а емкости конденсаторов С₁ = 2,0 мкФ и С₂ =3,0 мкФ. Конденсаторы зарядили до напряжения U=120 B и замкнули ключ К. Найти: а) период собственных колебаний; б) амплитудное значение тока через катушку.

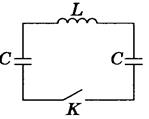
5. Электрическая цепь имеет пренебрежительно малое активное сопротивление. Левый конденсатор зарядили до напряжения U₀ и затем в момент t=0 замкнули ключ К. Найти зависимость от времени t напряжений на обоих конденсаторах.

6. В контуре совершаются свободные затухающие колебания, при которых напряжение на конденсаторе меняется во времени по закону U=U_m ∙e^-βt ∙ cos(ωt). Найти моменты времени, когда модуль напряжения на конденсаторе достигает: а) амплитудных значений; б) максимальных (экстремальных) значений.

7. Контур содержит конденсатор емкости С, катушку с индуктивностью L, и активным сопротивлением R, а также ключ. При замкнутом ключе конденсатор зарядили, после чего ключ замкнули и начались колебания. Найти отношение напряжения на конденсаторе к его амплитудному значению в момент непосредственно после замыкания ключа.

8. В колебательном контуре с индуктивностью L происходят свободные затухающие колебания, при которых ток меняется во времени по закону I = I_m ∙e^-βt ∙sin(ωt). Найти напряжение на конденсаторе в зависимости от времени и в момент t = 0.

9. Контур состоит из конденсатора емкости С = 4,0 мкФ и катушки с индуктивностью L = 2,0 мГн и активным сопротивление R = 10 Ом. Найти отношение магнитного поля катушки к энергии электрического поля конденсатора в момент максимума тока.

10. Контур содержит две последовательно соединённые катушки с активными сопротивлениями R₁ и R₂ и индуктивностями L₁ и L₂, причем взаимная индуктивность их пренебрежительно мала. Эти катушки надо заменить так, чтобы частота и добротность контура не изменилась. Найти индуктивность и активное сопротивление такой катушки.

11. Найти время, за которое амплитуда колебаний тока в контуре с добротностью Q = 5000 уменьшилась в η = 2,0 раза, если частота колебаний ν = 2,2 МГц.

12. Колебательный контур имеет емкость С = 10 мкФ, индуктивность L=25 мГн и активное сопротивление R =1,0 Ом. Через сколько колебаний амплитуда в этом контуре уменьшится в е раз?

13. На сколько процентов отличается частота ω свободных колебаний контура с добротностью Q = 5,0 от собственной частоты ω₀ колебаний этого контура?

14. Колебательный контур содержит конденсатор с утечкой. Емкость конденсатора С, его активное сопротивление R. Индуктивность катушки L. Сопротивление катушки и проводов пренебрежимо мало. Найти: а) частоту затухающих колебаний такого контура; б) его добротность.

15. Найти добротность контура с емкость С =2,0 мкФ и индуктивностью L = 5,0 мГн, если на поддержание в нем незатухающих колебаний с амплитудой напряжения на конденсаторе U_m = 1,0 В необходимо подводить мощность < Р > = 0,10 мВт. Затухание колебаний в контуре достаточно мало.

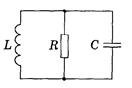
16. Какую среднюю мощность должен потреблять колебательный контур с активным сопротивлением R = 0,45 Ом, чтобы в нем поддерживались незатухающие гармонические колебания с амплитудой тока I _m = 30 мА? Колебательный контур содержит конденсатор емкостью С = 1,2 нФ и катушку с индуктивностью L = 6,0 мкГн и активным сопротивлением R = 0,50 Ом. Какую среднюю мощность нужно подводить к контуру, чтобы поддерживать в нем незатухающие гармонические колебания с амплитудой напряжения на конденсаторе U_m = 10 В? Найти частоту затухающих колебаний контура, показанного на рисунке. Емкость С, индуктивность L и активное сопротивление R предполагаются известными.

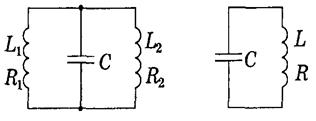17. Имеются два колебательных контура с конденсаторами одинаковой емкости. При каком соотношении между индуктивностями и активными сопротивлениями катушек частоты и затухания свободных колебаний в обоих контурах будут одинаковы? Взаимная индуктивность левого контура пренебрежимо мала.

18. Контур состоит из последовательно включенных конденсатора емкости С, катушки индуктивности L, ключа и сопротивления, равного критическому для данного контура. При разомкнутом ключе конденсатор зарядили до напряжения U₀ и в момент t = 0 ключ замкнули. Найти ток I в контуре как функцию времени t. Чему равен I_макс?

19. Катушку с активным сопротивлением R и индуктивностью L подключили в момент t = 0 к источнику напряжения U = U_m∙ cos(ωt). Найти ток в катушке I (t).

20. Цепь, состоящую из последовательно соединенных конденсатора емкости С и сопротивления R, подключили к переменному напряжению U =U_m ∙cos(ωt) в момент t = 0. Найти ток в цепи как функцию времени t .

21. Концы цепи, состоящей из последовательно включенных конденсатора и активного сопротивления R = 110 Oм, подключили к переменному напряжению с амплитудой U_m = 110 В. При этом амплитуда установившегося тока в цепи I_m = 0,50 A. Найти разность фаз между током и подаваемым напряжением.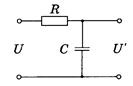

22. На рисунке показана простейшая схема сглаживания фильтра. На вход подают напряжение U . Найти: а) выходное напряжение U^’ (t); б) значение RC, при котором амплитуда переменной составляющей напряжения при выходе будет в η = 7,0 раз меньше постоянной составляющей, если ω = 314∙ с^-1

23. Колебательный контур с индуктивностью L подключен последовательно к внешнему синусоидальному напряжению с амплитудой U_m . Контур настроен в резонанс, при котором амплитуда установившегося тока равна I_m. Найти промежуток времени τ, за который амплитуда тока уменьшится в е раз, если процесс будет происходить в режиме свободных затухающих колебаний.

24. Цепь из последовательно соединенных конденсатора емкости С = 22 мкФ и катушки с активным сопротивлением R = 20 Ом и индуктивностью L = 0,35 Гн подключена к сети переменного напряжения с амплитудой U = 180 В и частотой ω = 314 с^-1. Найти: a) амплитуду тока в цепи; б) разность фаз между током и внешним напряжением; с) амплитуды напряжения на конденсаторе и катушке.

25. Цепь из последовательно соединенных конденсатора емкости С, катушки индуктивности L (без активного сопротивления) и резистора с сопротивлением R подключили к источнику гармоничного напряжения, частоту которого можно менять, не изменяя амплитуды. Найти частоту ω, при которой становится максимальным напряжение: а) на конденсаторе б) на катушке. Убедиться, что эти частоты связаны соотношениями: ω _Срез < ω_Lрез и ω_Срез· ω_Lрез = ω₀² .

26. Переменное напряжение с частотой ω = 314 с ^-1 и амплитудой U_m = 180 В подключено к концам цепи, состоящей из последовательно соединенных конденсатора и катушки с активным сопротивлением R = 40 Ом и индуктивностью L = 0,36 Гн. При каком значении емкости конденсатора амплитуда напряжения на катушке будет максимальной? Чему равна эта амплитуда и соответствующая амплитуда напряжения на конденсаторе?

27. Конденсатор емкости С, пространство между обкладками которого заполнено слабо проводящей средой с активным сопротивлением R, подключили к источнику переменного напряжения U = U_m ∙cos(ωt). Найти установившийся ток в подводящих проводах в зависимости от времени. Сопротивление проводов пренебрежимо мало. Колебательный контур содержит конденсатор емкости С и соленоид с индуктивностью L₁. Соленоид индуктивно связан с короткозамкнутой катушкой, имеющей индуктивность L₂ и пренебрежимо малое активное сопротивление. Их взаимная индуктивность L₁₂. Найти собственную частоту данного колебательного контура.

28. Найти добротность колебательного контура, в которой последовательно включен источник переменной ЭДС, если при резонансе тока напряжение на конденсаторе в n раз превышает напряжение на источнике.

29. Цепь переменного тока, состоящая из последовательно соединенных катушки и конденсатора, подключена к источнику переменной ЭДС, причем индуктивность катушки подобрана так, что ток в цепи максимален. Найти добротность системы, если известно, что при увеличении индуктивности в n раз ток в цепи уменьшается в η раз.

30. Последовательно соединенные конденсатор емкости С = 45 мкФ и катушка с активным сопротивлением подключены к источнику гармонического напряжения, частоту которого можно менять, не изменяя его амплитуды. При частотах ν₁ = 1,50 кГц и ν₂ = 2,50 кГц амплитуда тока оказалась одинаковой. Найти индуктивность катушки.

31. Показать, что при малом затухании добротность контура, в котором совершаются вынужденные колебания, Q ≈ ω /∆ ω , где ω₀ ─ cсобственная частота колебаний, ∆ω ─ ширина резонансной кривой I (t) на высоте, в √2 раз меньшей амплитуды тока при резонансе.

32.К концам цепи, состоящей из последовательно соединенных конденсатора и катушки, подают поочередно два переменных напряжения одинаковой амплитуды, но разной частоты. Частота одного напряжения равна собственной частоте ω₀, другого η в раз больше. Найти отношение амплитуд токов I₀/I, возбуждаемых обоими напряжениями, если добротность системы равна Q. Вычислить это отношение для Q = 10 и 100, если η = 1,10.

33. Соленоид с индуктивностью L = 7мГн и активным сопротивлением R = 44 Ом, подключили сначала к источнику постоянного напряжения U₀, а затем к генератору синусоидального напряжения с действующим значением U = U₀. При какой частоте генератора мощность, потребляемая соленоидом, будет в η = 5,0 раз меньше, чем в первом случае?

34. К сети с действующим напряжением U = 100 В подключили катушку, индуктивное сопротивление которой X_L = 30 Ом и импеданс Z = 50 Ом. Найти разность фаз между током и напряжением, а также тепловую мощность, выделяемую в катушке.

35. Катушка с индуктивностью L = 0,70 Гн и активным сопротивлением

R = 20 Ом, соединена последовательно с безындукционным сопротивлением R, и между концами этой цепи приложено переменное напряжение с действующим значением U = 220 В и частотой ω = 314 с^-1. При каком значении сопротивления R в цепи будет выделяться максимальная тепловая мощность? Чему она равна?

Тема 19 Волновые процессы

1. Найдите длину волны колебаний, период которых равен 10^-14с. Скорость распространения колебаний 3∙10⁸ м/с.

2. Звуковые колебания с частотой 500 Гц и амплитудой 0,25 мм распространяются в воздухе. Длина волны 70 см. Напишите уравнение этой волны.

3. Волна распространяется в среде со скоростью 100 м/с. Наименьшее расстояние между точками среды, фазы колебаний которых противоположны, равно 1 м. Найдите частоту колебаний и длину волны.

4. Найдите разность фаз колебаний двух точек в волне, находящихся на расстоянии 5 м друг от друга, если период колебаний 0,04 с, а скорость распространения колебаний 300 м/с.

5. Найдите смещение от положения равновесия точки, отстоящей от источника колебаний на расстоянии х = λ/12 в момент времени t =T/6, где λ - длина волны, а Т- период колебаний. Амплитуда колебаний равна 5 см.

6. Смещение от положения равновесия точки, колеблющейся на расстоянии 4 см от источника колебаний, вмомент t = Т/6 равно половине амплитуды. Найдите длину бегущей волны.

7. Расстояние между узлом и ближайшей к нему пучностью в стоячей волне равно 2 м. Найдите длину бегущей волны, из которой образовалась стоячая волна.

8. В источнике колебаний отношение максимального ускорения к максимальной скорости точки равно 5 с. Найти длину волны, распространяющуюся от этого источника, если скорость распространения колебаний 20 м/с.

9. Найдите, на каком расстоянии находится колеблющаяся точка от источника колебаний, если смещение точки от положения равновесия равно половине амплитуды в момент времени t = T/3, где Т- период колебаний. Длина волны 4 м.

10. Уравнение колебаний имеет вид: у = 4∙ sin (600π∙t) (см). Найдите смещение от положения равновесия точки, находящейся на расстоянии 75 см от источника колебаний, через 0,01 с после начала колебаний. Скорость волны 300 м/с.

11. Волна распространяется по прямой со скоростью 20 м/с. Две точки, находящиеся на этой прямой на расстоянии 12 м и 15 м от источника колебаний, колеблются с одинаковыми амплитудами, равными 0,1 м и разностью фаз 0,75π:.. Найдите длину волны и напишите уравнение волны.

Тема 20 Электромагнитные волны

1. Найдите среднее значение вектора Пойнтинга для плоской электромагнитной волны, распространяющейся в вакууме. Амплитуда напряженности электрического поля в волне 50 мВ/м.

2. Радиостанция мощностью 500 кВт излучает энергию 20 ч в сутки. Найдите массу, соответствующую энергии, излученной этой станцией за 30 суток.

3. Световая волна имеет частоту 4.10¹⁴ Гц и длину волны 5.10 ^-5см. Найдите скорость распространения волны в данном веществе и в вакууме, а также показатель преломления вещества.

4. В вакууме распространяется плоская электромагнитная волна, амплитуда электрической составляющей которой равна 50 мВ/м. Найти среднее значение плотности потока энергии. Электрическая постоянная ε0= 8,85.10^-12 Кл²/(Н.м²).

5. Напряженность электрического поля плоской электромагнитной волны, распространяющейся в вакууме, меняется по закону: Е = Е₀ ∙cos(ωπ - kx). Найдите величину вектора Пойнтинга.

6. Определите энергию, которую переносит за 1 минуту плоская электромагнитная волна, распространяющаяся в вакууме, через площадку 10 см² , расположенную перпендикулярно направлению распространения волны. Амплитуда напряженности электрического поля волны 1 мВ/м. (Период колебаний << 1 минуты).

7. Плоская гармоническая электромагнитная волна распространяется, в вакууме. Амплитуда напряженности электрического поля в волне 50 мВ/м. Найдите амплитуду плотности тока смещения.

8. В вакууме вдоль оси х распространяется плоская электромагнитная волна с интенсивностью, равной 21,2 мкВт/м² . Определите амплитуду напряженности электрического поля волны.

9. Электромагнитная волна с частотой 3 МГц переходит из вакуума в немагнитную среду с диэлектрической проницаемостью, равной 4. Найдите приращение ее длины волны.

10. В вакууме вдоль оси х распространяется плоская электромагнитная волна, амплитуда напряженности магнитного Поля которой равна 5 мА/м. Определите интенсивность волны.

11. Точечный источник излучает свет равномерно по всем направлениям. Найдите амплитуды напряженностей электрического и магнитного полей волны на расстоянии 10 м от источника света, если его мощность равна 100 Вт.

12. Напряженность электрического (E) и магнитного (Н) полей измеряются в единицах СИ в В/м и А/м, соответственно. Отношение Е /Н имеет размерность сопротивления (Ом) и называется волновым сопротивлением среды, в которой распространяется электромагнитная волна. Вычислите волновое сопротивление вакуума.

13. Плоская электромагнитная волна распространяется в вакууме. Амплитуда напряженности электрической составляющей волны 500 мВ/м, частота 100 Мгц. Найдите среднюю за период колебаний плотность потока энергии электромагнитной волны.

14. По прямому проводнику круглого сечения течет ток силой I. Найдите поток вектора Пойнтинга через боковую поверхность участка проводника, имеющего сопротивление R.

15. Средняя мощность излучения радиостанции, распространяющегося по полусфере с центром в точке расположения станции, составляет 0,1 МВт. Найдите величину вектора Пойнтинга в точке, находящейся на расстоянии 10 км от станции.

Тема 21 Волновая оптика

Интерференция

1. Свет с длиной волны 0,60 мкм падает нормально к поверхности тонкой мыльной пленки с показателем преломления, равным 1,33. Расстояние между соседними интерференционными полосами равно 4 мм. Найдите угол между поверхностями пленки.

2. На тонкий стеклянный клин падает в направлении нормали к его поверхности красный свет с длиной волны 0,60 мкм. Определите угол между поверхностями клина, если расстояние между соседними темными интерференционными полосами в отраженном свете равно 4 мм.

3. На мыльную пленку с показателем преломления, равным 1,33, падает нормально пучок белого света. Какова должна быть наименьшая толщина пленки, чтобы в отраженном свете пленка имела зеленый цвет? Среднюю длину волны для зеленого цвета принять равной 550 нм.

4. Найдите длину волны света, если в опыте Юнга расстояние от первого интерференционного максимума до центральной полосы равно 0,5 мм. Расстояние между щелями 5 мм, расстояние от экрана, на котором наблюдается интерференционная картина, до щелей равно 5 м.

5. Два когерентных источника света, расстояние между которыми 0,2 мм, расположены от экрана на расстоянии 1,5 м. Найдите длину световой волны, если третий минимум интерференционной картины расположен на экране на расстоянии 12 мм от центра.

6. На плоскопараллельную тонкую пленку с показателем преломления 1,45 падает нормально пучок белого света. При какой наименьшей толщине пленка будет наиболее прозрачна для красного света с длиной волны 0,65 мкм?

7. От двух когерентных источников света с длиной волны 0,70 мкм на экране наблюдается интерференционная картина. Когда на пути одного из лучей перпендикулярно ему поместили мыльную пленку с показателем преломления, равным 1,33, интерференционная картина поменялась на противоположную. Определите наименьшую толщину пленки, при которой это возможно.

8. Найдите расстояние между двадцатым и двадцать первым светлыми кольцами Ньютона, если расстояние между вторым и третьим кольцами равно 1 мм, а кольца наблюдаются в отраженном свете.

9. На пути одного луча в интерференционной установке Юнга стоит трубка длиной 2 см, наполненная воздухом с показателем преломления 1,000276.. Наблюдения производятся в свете с длиной волны 0,60 мкм. Когда трубку заменили на другую таких же размеров, но заполненную хлором, то интерференционная картина сместилась на 20 полос. Определите показатель преломления хлора.

10. Найдите минимальную толщину пленки с показателем преломления 1,33, при которой свет с длиной волны 0,64 мкм испытывает максимальное отражение, а свет с длиной волны 0,40 мкм не отражается вовсе. Угол падения света на пленку 30°.

11. Плоско-выпуклую линзу с радиусом кривизны 12,5 см поместили выпуклой стороной на стеклянную пластинку. Диаметры десятого и пятнадцатого колец Ньютона в отраженном свете оказались равными 1,0 мм и 1,5 мм, соответственно. Найдите длину волны света.

12. Кольца Ньютона наблюдаются между плоско-выпуклой линзой и стеклянной пластинкой при освещении желтым светом с длиной волны 0,59 мкм, падающим параллельно оси линзы. При измерениях в отраженном свете расстояние между первым и вторым светлыми кольцами оказалось равным 0,5 мм. Найдите радиус кривизны линзы.

Дифракция

1. При нормальном падении света на дифракционную решетку угол дифракции для света с длиной волны 0,65 мкм в спектре второго порядка равен 45°. Найдите угол дифракции для света с длиной волны 0,50 мкм в спектре третьего порядка.

2. Свет с длиной волны λ падает нормально на дифракционную решетку. Найдите угловую дисперсию решетки в зависимости от угла наблюдения φ.

3. Для какой длины волны света дифракционная решетка имеет угловую дисперсию, равную 6,3.10⁵ рад/м в спектре третьего порядка, если постоянная решетки равна 5 мкм?

4. Постоянная дифракционной решетки в 2 раза больше длины волны световой волны монохроматического света, нормально падающего на ее поверхность. Определите угол между первыми симметричными дифракционными максимумами,

5. На дифракционную решетку нормально падает свет от источника с линейчатым спектром. Отношение синусов углов, под которыми наблюдаются две линии в спектре 2-го порядка, равно sinθ1/ sin2θ=1,709. Какова длина волны первой линии, если длина волны второй линии равна 0,546 нм?

6. На дифракционную решетку падает нормально свет с длиной волны 0,60 мкм. Найдите число щелей решетки, приходящихся на 1 мм, если спектральная линия во втором порядке спектра наблюдается под углом 30°.

7. Дифракционная решетка содержит 200 штрихов на 1 мм. На решетку падает нормально монохроматический свет с длиной волны 0,50 нм. Максимум какого наибольшего порядка дает эта решетка?

8. Найдите наибольший порядок спектра для длины волны 0_,60 мкм, если постоянная дифракционной решетки равна 2,4 мкм

9. Монохроматический свет падает нормально на щель шириной 11 мкм. За щелью вблизи ее помещена линза с фокусным расстоянием 150 мм, в фокальной плоскости которой расположен экран. Найдите длину волны света, если расстояние между симметрично расположенными минимумами третьего порядка на экране равно 50мм.

10. На дифракционную решетку, содержащую 500 штрихов на 1 мм, падает нормально белый свет. Спектр проецируется на экран линзой с фокусным расстоянием 3 м, помещенной вблизи решетки. Определите ширину спектра первого порядка. Границы видимого спектра электромагнитных волн составляют 400 нм - 700 нм.

11. Дифракционная картина получена с помощью дифракционной решетки длиной 1,95 см и периодом 5 мкм. Найдите наименьший порядок спектра, в котором две спектральные линии с разностью длин волн 0,1 нм наблюдаются раздельно, если они находятся вблизи длины волны, равной 780 нм.

12. Свет падает нормально на дифракционную решетку шириной 6,5 см. Найдите наименьшую разность длин волн, которую может разрешить эта решетка в области длин волн вблизи 670 нм.

13. Белый свет (диапазон длин волн 0,40 - 0,70 мкм) падает нормально на дифракционную решетку, имеющую 8000 штрихов на 1 см. Найдите ширину спектра третьего порядка на экране, находящемся на расстоянии 2,20 м от решетки.

14. При нормальном падении света на дифракционную решетку с периодом 0,05 мкм обнаружено, что можно разрешить в третьем порядке дублет спектральной линии вблизи длины волны 0,46 мкм, компоненты которого отличаются по длинам волн на 0,00013 мкм. Какова ширина этой решетки?

15. На щель падает нормально параллельный пучок монохроматического света с длиной волны λ. Ширина щели равна 6λ. Под каким углом будет наблюдаться третий дифракционный минимум света?

16. Свет падает нормально на дифракционную решетку с шириной 6,5 мм и периодом, равным 1/200 мм. В спектре какого порядка будут разрешены две компоненты спектральной линии, лежащей вблизи 670,8 нм, если они отличаются по длинам волн на 0,015 нм?

17. Какой наименьшей разрешающей способностью должна обладать дифракционная решетка, чтобы с ее помощью можно было наблюдать раздельно две спектральные линии калия с длинами волн 0,578 мкм и 0,580 мкм?

Поляризация

1. Под каким углом нужно отразить луч естественного света от кристалла каменной соли, показатель преломления которой равен 1,544, чтобы получить максимальную поляризацию отраженного луча?

2. Предельный угол полного внутреннего отражения света на границе жидкости с воздухом равен 45^е. Определить угол Брюстера для падения луча из воздуха на поверхность жидкости.

3. Под каким углом к горизонту должно находиться Солнце, чтобы его лучи после отражения от поверхности озера были полностью поляризованы? Диэлектрическая проницаемость воды для высокочастотного электрического поля считать равной 1,73.

4. Во сколько раз уменьшится интенсивность естественного света, если на его пути установить два поляроида, угол между плоскостями поляризации которых равен 60°? Считать, что поляроид пропускает 50 % падающего на него естественного света.

5. Луч света переходит из глицерина (показатель преломления 1,4) в стекло (показатель преломления 1,5) так, что луч, отраженный от границы раздела этих сред оказывается полностью поляризованным. Определите угол между падающим и преломленным лучами.

6. Пучок света падает из воздуха на поверхность жидкости под углом 56,3°. Определите угол преломления пучка, если отраженный свет полностью поляризован. Показатель преломления жидкости равен 1,5.

7. Чему равен угол полной поляризации для вещества, у которого угол полного внутреннего отражения равен 45°?

8. Покажите, что при падении света на границу двух диэлектриков под углом Брюстера отраженный и преломленный лучи взаимно перпендикулярны.

9. Естественный свет падает на поверхность стеклянной пластины, погруженной в жидкость. Отраженный от пластины луч образует угол 90° с падающим лучом. Определите показатель преломления жидкости, если отраженный луч полностью поляризован.

10. Пучок естественного света падает на систему из N поляризаторов, плоскость пропускания каждого из которых повернута на угол 30° относительно плоскости пропускания предыдущего поляризатора. При этом через систему проходит 12 % падающего на систему света. Найдите число поляризаторов.

11. При падении естественного света на некоторый поляризатор проходит 40% светового потока, а через два таких поляризатора - 4%. Найти угол между плоскостями пропускания этих поляризаторов.

12. Естественный свет падает на систему из 4-х поляризаторов, плоскость пропускания каждого из которых повернута на угол 60° относительно плоскости пропускания предыдущего поляризатора. Какая часть светового потока проходит через эту систему?

13. Найти коэффициент поглощения естественного света в поляроидах, если при угле 45° между их плоскостями поляризации через систему проходит 20% падающего света.

14. На сколько процентов уменьшается интенсивность естественного света после прохождения через призму Николя, если потери света составляют 10 %?

15. Плоскополяризованный свет интенсивности I0проходит последовательно через два поляризатора. Плоскость колебаний, пропускаемых первым поляризатором, составляет угол α₁с плоскостью колебаний падающего света, второго поляризатора - угол α₂. Определить интенсивность света, прошедшего через оба поляризатора.

Литература

1. Трофимова Т.И. Курс физики. М: Высш. шк., 2004. – 478 с.

2. Детлаф А.А., Яворский Б.М. Курс физики-М.:Высш. шк., 2002.-728 с. Иродов И.Е. Задачи по общей физике. – М.: Лаборатория Базовых Знаний, 2001. – 432 с.

3. Савельев И.В. Курс общей физики. В 3-х т. Т.2. Электричество и магнетизм. Волны. Оптика. – М.: Наука, 1982. – 496 с.

4. Чертов А.Г., Воробьев А.А. Задачник по физике. – М.: Высш. Шк., 1988. – 527 с.

5. Иродов И.Е. Задачи по общей физике. – М.: Лаборатория Базовых Знаний, 2001. – 432 с.

6. Сивухин Д.В. Общий курс физики. – М.: Наука, 1979-1989, Т.3-4