Раздел 2. Второе начало термодинамики
Первое начало термодинамики не дает никаких указаний относительно направления, в котором могут происходить процессы в природе. Пусть изолированная система состоит из двух тел, взаимодействующих между собой. В каком направлении будет переходить тепло от одного тела к другому – на этот вопрос первое начало термодинамики ответить не может. Второе начало термодинамики позволяет судить о направлении процессов, которые могут происходить в действительности. Основоположником второго начала термодинамики считается французский инженер и физик Сади Карно. В своём сочинении «О движущей силе огня и о машинах, способных развивать эту силу», вышедшем в 1834 г. (значительно ранее открытия первого начала Р. Майером, Джоулем и Гельмгольцем), он исследовал превращения теплоты в работу.
§2.1. Тепловые машины.
Тепловые машины или тепловые двигатели предназначены для получения полезной работы за счет теплоты, выделяемой при сгорании топлива (химических реакций), ядерных превращений или по другим причинам (например, вследствие нагрева солнечными лучами). Все тепловые машины можно разделить на два типа. Машины первого типа выполняют полезную работу за счет последовательности круговых циклов. К таким машинам относятся: паровые машины, паровые и газовые турбины, компрессоры, двигатели внутреннего сгорания и.т.д.. В итоге каждого цикла машина возвращается в первоначальное состояние. Машины второго типа совершают некруговые процессы, производя при этом полезную работу. В подобных устройствах машина – некоторая система, находящаяся первоначально в неравновесном состоянии, приходит в состояние равновесия. Переход в равновесное состояние сопровождается совершением полезной работы. К таким машинам относятся все устройства однократного действия. Чаше всего в таких устройствах полезная работа производится за счет химических реакций, протекающих в системе (например: гальванические элементы, ракеты). Для работы тепловой машины первого типа обязательно необходимы следующие составляющие: нагреватель, холодильник и рабочее тело. При этом, если необходимость в наличии нагревателя и рабочего тела обычно не вызывает сомнений, то холодильник как составная часть тепловой машины в её конструкции зачастую отсутствует. В качестве холодильника выступает окружающая среда. Принцип действия тепловых машин заключается в следующем. Нагреватель передает рабочему телу теплоту, вызывая повышение его температуры Q1. Рабочее тело (газ) совершает работу над каким-либо механическим устройством, например, приводит во вращение турбину, и далее отдает холодильнику теплоту Q2, возвращаясь в исходное состояние.
В соответствии с первым началом термодинамики, при осуществлении кругового процесса, из-за возвращения рабочего тела в исходное состояние, его внутренняя энергия за цикл не изменяется. Поэтому совершенная рабочим телом механическая работа равна разности подведенной и отведенной теплоты:
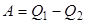 . . | (2.1) |
Таким образом, тепловая машина совершила круговой процесс, в результате которого нагреватель отдал тепло Q1, холодильник получил тепло Q2, тепло Q=Q2-Q1 пошло на производство работы A1-A2.
Отношение
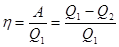 | (2.2) |
называется коэффициентом полезного действия тепловой машины.
Рассмотрим схематически цикл, по которому осуществляется работа тепловой машины первого типа. Схематически тепловая машина изображена на рис.5.а. В цилиндре машины помещается вещество, называемое рабочим телом. Для определенности будем считать, что рабочим телом является газ. Круговой процесс, происходящей в направлении часовой стрелки, представляет собой схему работы любой тепловой машины, трансформирующей тепло в работу.
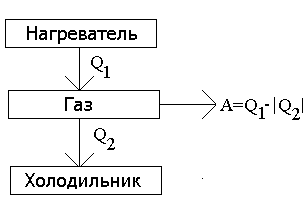 | 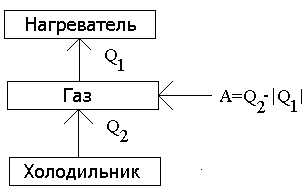 |
| Рис.5.а | Рис.5.б |
Если мы теперь рассмотрим цикл, который происходит в обратном направлении против часовой стрелки, то переменятся на обратные и знаки количества тепла и работы. Мы получим схему работы холодильной машины, над которой совершается работа (см. Рис.5.б), но при этом тепло от менее нагретого тела переходит к более нагретому телу.
Из различных круговых процессов особое значение в термодинамике имеет цикл Карно. Это квазистатический процесс, в котором систему можно приводить в тепловой контакт без теплового обмена с внешней средой (адиабаттически) с двумя тепловыми резервуарами, имеющими постоянные температуры Т1 и Т2. Тепловой резервуар с более высокой температурой Т1 называется нагревателем, а с более низкой температурой Т2 - холодильником. Цикл Карно заключается в следующем. Сначала система, имея температуру Т1, приводится в тепловой контакт с нагревателем. Затем, бесконечно медленно уменьшая внешнее давление, система квазистатически расширяется по изотерме 12 (рис.6.). При этом она заимствует тепло Q1 от нагревателя и производит работу А12 против внешнего давления. После этого систему адиабатически
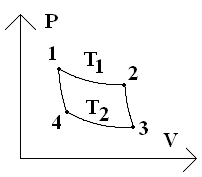 |
| Рис. 6. |
изолируют, и она продолжает квазистатически расширяться по адиабате 23, пока её температура не достигнет температуры холодильника Т2. При адиабатическом расширении система также совершает некоторую работу А23 против внешнего давления. В состоянии 3 систему приводят в тепловой контакт с холодильником и непрерывном увеличении давления изотермически сжимают её до некоторого состояния 4. При этом над системой производится работа (сама система совершает отрицательную работу A34), и она отдает холодильнику некоторое количество тепла Q2. Состояние 4 выбирается так, чтобы можно было квазистатическим сжатием по адиабате 41 вернуть систему в исходное состояние. Для этого над системой надо совершить работу (т.е. система должна произвести отрицательную работу А41). Таким образом, суммарная работа равна:
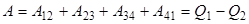 . . | (2.3) |
Сади Карно, изучая работу тепловых машин, сформулировал две теоремы:
1. Коэффициент полезного действия любой обратимой тепловой машины, работающей по циклу Карно, не зависит от природы рабочего тела и устройства машины, а является функцией только температуры нагревателя и холодильника:
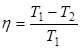 . . | (2.4) |
2. Коэффициент полезного действия любой тепловой машины, работающей по необратимому циклу, меньше коэффициента полезного действия машины с обратимым циклом Карно, при условии равенства температур их нагревателей и холодильников.
§2.2. Формулировки второго начала термодинамики.
Формула (2.2) показывает, что к.п.д. не может быть больше единицы, но сама по себе она не исключает возможности равенства h единице. Это может произойти, если теплота, поступившая от нагревателя в машину, полностью превращается в работу. Принципом Кельвина называется утверждение о том, что: «Невозможен круговой процесс, единственным результатом которого было бы производство работы за счет охлаждения теплового резервуара». Это одно из выражений второго начала термодинамики. Другая из возможных формулировок второго начала термодинамики принадлежит Клаузиусу: невозможен циклический процесс, единственным результатом которого была бы передача теплоты от менее нагретого тела к более нагретому. В такой формулировке справедливость второго начала термодинамики почти очевидна: трудно представить себе ситуацию, когда не произошло никаких изменений, а некоторое количество теплоты как бы само собой перешло от тела с меньшей температурой, которое охладилось, к телу с большей температурой, которое еще больше нагрелось. Предположим, что такой процесс возможен. Взяв простейшую тепловую машину, произведем круговой процесс, в результате которого машина, получив от нагревателя тепло Q1, передаст холодильнику тепло Q2 и, при этом совершит положительную работу A=Q1-Q2. Затем вернем тепло Q2 от холодильника нагревателю. В результате, реализован круговой процесс, единственным результатом которого является производство работы А за счет охлаждения теплового резервуара. Но такой процесс отрицается принципом Кельвина, следовательно, мы показали, что формулировки второго начала термодинамики Кельвина и Клаузиуса эквивалентны.
Формулировка Клаузиуса не утверждает, что передача тепла от тела менее нагретого к телу более нагретому невозможна вообще. Она невозможна при условии, что во всех остальных телах никаких изменений не происходит. В этом смысл слова «самопроизвольно», употребленного при формулировке второго начала термодинамики. Если же допустить другие процессы, то передача тепла от тела менее нагретого к телу более нагретому становится возможной. Такие процессы называются компенсирующими процессами или, компенсациями. Так, в холодильных машинах тепло, полученное от менее нагретого тела, передается более нагретому телу. Это не противоречит формулировке Клаузиуса, так как такой переход сопровождается работой электрического мотора.
Задача 2.1.Доказать, что коэффициент полезного действия тепловой машины, работающей по циклу Карно равен 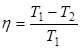 .
.
Решение. Цикл Карно состоит из двух изотерм 1-2 и 3-4, которым соответствуют температуры Т1 и Т2 и двух адиабат 2-3, 4-1 (рис.1.2.). В этом цикле рабочим веществом является идеальный газ. Передача количества теплоты от нагревателя рабочему веществу происходит при температуре Т1, а от рабочего вещества к холодильнику – при температуре Т2.
Определим к.п.д. цикла Карно.
При температуре Т1 нагреватель передает тепло рабочему телу (см. таблицу)
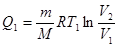
При температуре Т2 в процессе 3-4 тепло передается холодильнику
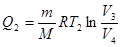
Отсюда к.п.д. цикла Карно равен:
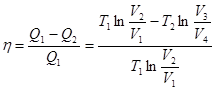
Логарифм отношения объемов определим из уравнений адиабатических процессов.
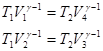
Поделим выражения друг на друга, получим, что
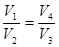 .
.
Следовательно, логарифмы отношений объемов V2/V1 и V3/V4 равны и к.п.д. цикла Карно определяется только температурами холодильника и нагревателя и не зависит от рабочего вещества и конструкции машины, совершающей цикл.
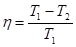 |
Задачи для самостоятельного решения:
Задача. 2.2.Идеальный газ (n=1 кмоль) совершает циклический процесс, изображенный двумя изохорами и двумя изобарами. При этом объем газа изменяется от V1=25 м3 до V2=50 м3, а давления изменяется от p1=100 кПа до p2=200 кПа. Во сколько раз работа, совершаемая при таком цикле, меньше работы, совершаемой в цикле Карно, изотермы которого соответствуют наибольшей и наименьшей температурам рассматриваемого цикла, если при изотермическом расширении объем увеличился в два раза?
Ответ: 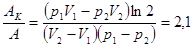
Задача. 2.3.Один киломоль идеального двухатомного газа находился под давлением p1=100кПа при температуре Т1=300К. После нагревания в изохорном процессе давление газа стало равным p2=200кПа. После этого газ изотермически расширялся до давления Р1, а затем был изобарически сжат до начального объема V1. Определите температуру изотермического процесса и КПД цикла.
Ответ: Т2=600К, h=0,1.
Задача. 2.4. Определите температуру Т в камере холодильника, если количество сообщенной теплоты в e=5 раз превышает энергию, затраченную на работу. Холодильник работает по циклу Карно. Температура воздуха в комнате T0=293K.
Ответ: 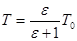
Задача. 2.5. Цикл Карно осуществляется в интервале температур T1=600K и T2=200К. Давление в конце изотермического расширения и в начале адиабатического сжатия одинаково. Рабочим телом является воздух. Определите полезную работу, совершаемую воздухом ( m=1 кг) за цикл.
Ответ: 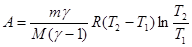 =4.41·105 Дж.
=4.41·105 Дж.
Задача 2.6.Идеальный газ совершает цикл, состоящий из изотермы, политропы и адиабаты, причем изотермический процесс происходит при максимально температуре цикла. Найти к.п.д. такого цикла, если температура Т в его пределах изменяется в n раз.
Ответ: h=1-(n-1)/(n·ln n)
Энтропия.
Разделив обе части равенства, выражающего первое начало термодинамики на Т, получим:
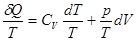 , , | (2.5) |
где dQ/T – приведенная теплота. Подставляя в (2.5) p/T=R/V и учитывая, что dT/T=d lnT, dV/V= d lnV, находим:
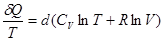 . . | (2.6) |
Правая часть равенства представляет собой полный дифференциал. Следовательно, левая часть dQ/T также полный дифференциал. Функция состояния, дифференциалом которой является dQ/T, называется энтропией и обозначается S. Таким образом:
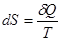 . . | (2.7) |
Для термодинамической системы, совершающей квазистатический циклический процесс, в котором система получает малое количество теплоты dQ при соответствующих значениях абсолютной температуры Т, интеграл от приведенного количества теплоты по всему замкнутому циклу равен нулю (т.н. равенство Клаузиуса 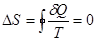 ).
).
Совместное применение первой и второй теорем Карно позволяет получить следующее неравенство:
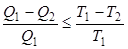 . . | (2.8) |
Знак равенства в этой формуле соответствует случаю описания обратимой тепловой машины, а знак меньше - описанию необратимой тепловой машины.
Формулу (2.8) можно преобразовать к виду:
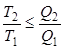 . . | (2.9) |
Тогда,
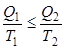 . . | (2.10) |
или
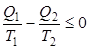 . . | (2.11) |
Если полученное выражение записать через количество теплоты, подводимой к рабочему телу от нагревателя и холодильника Q2=-Q2’, то оно примет вид:
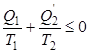 . . | (2.12) |
Формула (2.12) представляет собой частный случай неравенства Клаузиуса.
Для необратимых процессов интеграл от приведенной теплоты dQ/T по замкнутому пути всегда отрицателен 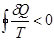 , энтропия возрастает (т.н. неравенство Клаузиуса). Неравенство Клаузиуса (2.12) позволяет отличать обратимые и необратимые круговые термодинамические процессы. В случае, если термодинамический цикл состоит только из обратимых процессов, неравенство переходит в равенство Клаузиуса. Случай строгого неравенства в формуле (2.12) соответствует описанию необратимых круговых термодинамических процессов, и это выражение применяется в неравновесной термодинамике. Необходимо также заметить, что формула (2.7) дает определение разности энтропий, но не ее абсолютное значение. С помощью этой формулы можно вычислить, чему равно изменение энтропии при переходе из одного состояния в другое, но нельзя сказать, чему равна энтропия в каждом из состояний, т.е. энтропия определена с точностью до произвольной аддитивной постоянной.
, энтропия возрастает (т.н. неравенство Клаузиуса). Неравенство Клаузиуса (2.12) позволяет отличать обратимые и необратимые круговые термодинамические процессы. В случае, если термодинамический цикл состоит только из обратимых процессов, неравенство переходит в равенство Клаузиуса. Случай строгого неравенства в формуле (2.12) соответствует описанию необратимых круговых термодинамических процессов, и это выражение применяется в неравновесной термодинамике. Необходимо также заметить, что формула (2.7) дает определение разности энтропий, но не ее абсолютное значение. С помощью этой формулы можно вычислить, чему равно изменение энтропии при переходе из одного состояния в другое, но нельзя сказать, чему равна энтропия в каждом из состояний, т.е. энтропия определена с точностью до произвольной аддитивной постоянной.
Применим формулу (2.7) для вычисления изменения энтропии в изотермическом процессе, где температура газа остается неизменной, а всевозможные изменения термодинамических характеристик обусловлены лишь изменением объема. Для этого случая dS=R·dlnV. И, следовательно, после интегрирования S2-S1=R(lnV2-lnV1). Для дальнейшего преобразования выражения, стоящего в правой части, необходимо принять во внимание связь объема, который занимает газ в равновесном состоянии, с числом пространственных микросостояний частиц газа. Число частиц в моле газа равно постоянной Авогадро NA. Равновесное состояние осуществляется наибольшим числом способов реализации этого состояния.
Термодинамическую вероятностью G или статистическую сумму можно определить как число микросостояний, реализующих данное макросостояние. Для изотермического процесса число микросостояний определяется количеством способов размещений частиц в объеме системы. Таким образом, можно записать, что 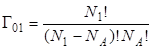 и
и 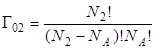 . С использованием формулы Стирлинга (при больших n выполняется равенство
. С использованием формулы Стирлинга (при больших n выполняется равенство 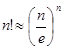 ) получаем:
) получаем: 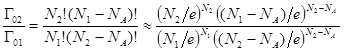 . Исследуя не слишком сжатый газ, когда N1 и N2 много больше, чем NA, тогда получаем:
. Исследуя не слишком сжатый газ, когда N1 и N2 много больше, чем NA, тогда получаем:
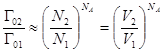 . Логарифмируя выражение, находим, что
. Логарифмируя выражение, находим, что 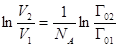 . Подставляя это выражение в S2-S1=R(lnV2-lnV1), приводим его к виду S2-S1=k(lnG02-lnG01). Вид формулы наводит на мысль, что энтропия определяется логарифмом числа микросостояний, посредством которых реализуется рассматриваемое макросостояние:
. Подставляя это выражение в S2-S1=R(lnV2-lnV1), приводим его к виду S2-S1=k(lnG02-lnG01). Вид формулы наводит на мысль, что энтропия определяется логарифмом числа микросостояний, посредством которых реализуется рассматриваемое макросостояние:
| S=klnG | (2.8) |
Это равенство называется формулой Больцмана. Вышеприведенные рассуждения не являются доказательством формулы Больцмана. Формула (2.8) позволяет дать энтропии очень наглядное толкование. Чем сильнее упорядочена система, тем меньше число микросостояний, которым осуществляется макросостояние. Энтропия – мера упорядоченности системы. Будучи предоставлена самой себе, система стремится к равновесному состоянию, а поскольку равновесное состояние – наиболее вероятное, т.е. соответствует максимуму термодинамической вероятности, то стремление системы к равновесию тождественно означает возрастание энтропии S к своему максимальному значению при заданных внешних условиях.
Применим неравенство Клаузиуса для описания необратимого кругового термодинамического процесса. Пусть процесс 1→2 будет необратимым, а процесс 2→1 - обратимым. Тогда неравенство Клаузиуса для этого случая примет вид
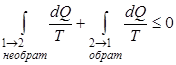 . . | (2.13) |
Так как процесс является обратимым, для него можно воспользоваться соотношением 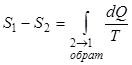 , подставляя его в (2.13), получаем:
, подставляя его в (2.13), получаем:
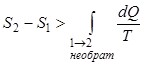 . . | (2.14) |
Для обратимых и необратимых процессов можно записать закон возрастания энтропии:
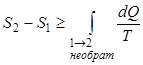 , , | (2.14) |
в котором знак равенства имеет место в случае, если процесс 1→2 является обратимым, а знак больше, если процесс 1→2 - необратимый.
Полученные неравенства выражают собой закон возрастания энтропии, который можно сформулировать следующим образом:
В адиабатически изолированной термодинамической системе энтропия не может убывать: она или сохраняется, если в системе происходят только обратимые процессы, или возрастает, если в системе протекает хотя бы один необратимый процесс.
Записанное утверждение является ещё одной формулировкой второго начала термодинамики. Таким образом, изолированная термодинамическая система стремится к максимальному значению энтропии, при котором наступает состояние термодинамического равновесия.
В качестве иллюстрации рассмотрим следующий пример. Пусть один моль идеального газа заключен в цилиндр с твердыми адиабатическими стенками. Цилиндр разделен на две части твердой перегородкой AB. Сначала газ занимает одну из этих частей с объемом V1. Во второй части - вакуум. Затем перегородка убирается. Газ начинает перетекать во вторую часть цилиндра, пока не выровняются давление и температура в обеих частях. Вычислим изменение энтропии газа. В результате описанного процесса внутренняя энергия газа не меняется, так как он заключен в жесткую адиабатическую оболочку. Не меняется и температура газа, поскольку она однозначно определяется его внутренней энергией. Обозначим через V2 – конечные объемы газа. Чтобы вычислить изменение энтропии газа, надо перевести его из начального состояния в конечное квазистатически. Это можно сделать, приведя газ в тепловой контакт с нагревателем, имеющим температуру Т. Бесконечно медленно уменьшая давление на газ, можно его изотермически перевести в конечное состояние с объемом V2. При этом газ будет заимствовать тепло от нагревателя и превращать его в эквивалентную работу. Для изотермического процесса: 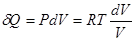 . А
. А 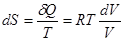 . Отсюда
. Отсюда 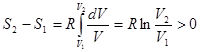 .
.
Энтропия возросла. Поэтому адиабатическое расширение газа в пустоту – необратимый процесс.
Обратим внимание на довольно распространенную ошибку. Говорят, что если теплота не подводится, т.е. dQ=0, то и dS=dQ/T=0. Отсюда заключают, что S=const. Ошибка заключается в том, что равенством dS=dQ/T можно пользоваться в случае только квазиравновесных процессов. Для неравновесных процессов это равенство не имеет места. Для определения разности энтропий интеграл должен быть взят для произвольного, но обязательно квазистатического процесса, переводящего систему из начального состояния в конечное.
Необходимо отметить, что если система не является изолированной, то в ней возможно уменьшение энтропии. Примером такой системы может служить, например, обычный холодильник, внутри которого возможно уменьшение энтропии. Но для таких открытых систем это локальное понижение энтропии всегда компенсируется возрастанием энтропии в окружающей среде, которое превосходит её локальное уменьшение.
Задача 2.7. При нагревании двухатомного газа (n=1 кмоль) его абсолютная температура увеличивается в х=1,5 раза. Найти изменение энтропии, если нагревание происходит: а) изохорно; б) изобарно.
Решение. Изменение энтропии можно определить, используя уравнение (3.3). При изохорном процессе, объем не изменяется, работа не совершается.
dQ=dU
Тогда изменение энтропии в процессе а) можно сосчитать по формуле:
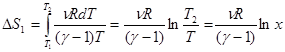
Постоянную адиабаты g можно определить из (1.5), зная, что для двухатомного газа количество степеней свободы равно i=5, g=1.4.
Для изобарического процесса, изменение энтропии можно сосчитать, выразив давление из уравнения Менделеева – Клапейрона 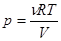 .
.
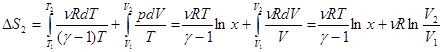
Так как при изобарическом процессе отношение давлений равно отношению температур, то при изобарическом процессе изменение энтропии определяется выражением:
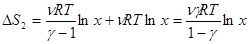 .
.
Задача 2.8. Два баллона емкостью V1 и V2соединены трубкой с краном, и оба заполнены кислородом. Давление в сосудах соответственно p1 и p2. Найти изменение энтропии системы в результате перемешивания газов после открытия крана. Вся система изолирована. Начальная температура в баллонах одинакова и равна Т0. При данных давлениях и температуре газ близок по своим свойствам к идеальному.
 Решение. В случае равенства давлений p1=p2 при открытии крана молекулы газа из первого баллона могут переместиться во второй и наоборот, но так как молекулы неразличимы между собой, мы этого не заметим. Закрыв кран, мы будем иметь ту же картину, что и в начале задачи. Энтропия системы остается постоянной. Теперь рассмотрим случай, когда давления в баллонах разные. Смешивание происходит адиабатически, но необратимым образом, поэтому энтропия системы должна возрастать. Что произойдет, если мы откроем кран? Внутренняя энергия идеального газа зависит только от температуры. Так как система изолирована, внутренняя энергия газа остается постоянной. В конечном состоянии мы будем иметь газ при температуре Т0и некотором давлении р. Так как молекулы газа в первом и во втором баллонах неразличимы между собой мы можем кран заменить поршнем, который будет перемещаться обратимым образом при Т0=const, пока не выровняется давление.
Решение. В случае равенства давлений p1=p2 при открытии крана молекулы газа из первого баллона могут переместиться во второй и наоборот, но так как молекулы неразличимы между собой, мы этого не заметим. Закрыв кран, мы будем иметь ту же картину, что и в начале задачи. Энтропия системы остается постоянной. Теперь рассмотрим случай, когда давления в баллонах разные. Смешивание происходит адиабатически, но необратимым образом, поэтому энтропия системы должна возрастать. Что произойдет, если мы откроем кран? Внутренняя энергия идеального газа зависит только от температуры. Так как система изолирована, внутренняя энергия газа остается постоянной. В конечном состоянии мы будем иметь газ при температуре Т0и некотором давлении р. Так как молекулы газа в первом и во втором баллонах неразличимы между собой мы можем кран заменить поршнем, который будет перемещаться обратимым образом при Т0=const, пока не выровняется давление.
Первое начало термодинамики можно записать в следующем виде
.
Постоянство внутренней энергии дает соотношение:
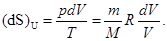
В силу аддитивности энтропии, ее общее изменение представится суммой изменений для каждого баллона
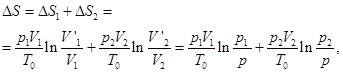
где 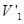 и
и 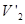 - объемы после выравнивания давлений. Записав очевидные соотношения
- объемы после выравнивания давлений. Записав очевидные соотношения
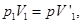
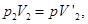
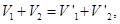
имеем
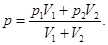
Таким образом,