Фізика атома
· Момент імпульсу електрона на орбіті в атомі:
,
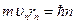де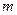 
– маса електрона; 
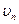– швидкість електрона на n – ній орбіті; 
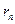– радіус n – ної орбіти; 
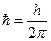, де 
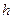– стала Планка.
· Радіус n – ної стаціонарної орбіти:
,
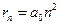де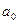 
– перший борівський радіус:
,
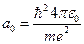а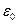 
– електрична стала.
· Енергія електрона на n – ній орбіті в атомі водню:
,
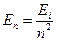де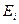 
– енергія іонізації атома водню.
· Енергія, яку випромінює чи поглинає атом:
,
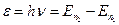· Частота хвилі, що випромінюється в спектрі водневоподібних атомів:
,
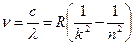де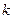 
=1, 2, 3, 4, 5, 6 і визначає серію випромінюівння; 
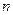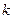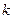= +1, +2, 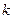+3… – визначає окремі лінії серії; 
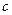– швидкість світла у вакуумі; 
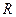– стала Рідберга.
· Формула Фульфа–Брегга:
, 
,
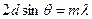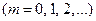де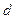 
– міжплощинна відстань; 
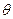– кут між пучком рентгенівськиї променів і поверхнею кристала.
· Короткохвильова границя суцільного рентгенівського спектру:
,
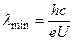де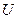 
– прискорюючи різниця потенціалів.
· Закон Мозлі для характеристичного рентгенівського спектру:
,
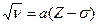У рамках моделі атома Бора:
,
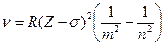де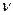 
– частота; 
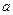– стала для певної серії ліній; 
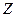– атомний номер елемента; 
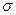– стала екранування (для 
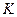– серії 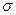= 1, для 
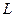– серії 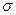= 7,5); 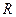– стала Ридберга; 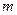і 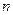– номери атомних рівнів.
16.1. Виразити через сталу Рідберга і частоту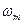 
головної лініі М - ної спектральної серії водневого атома.
16.2. Потенціал іонізації водневоподібного атома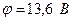 
. Обчислити значення сталої Рідберга.
16.3. Енергія іонізації атома водню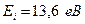 
. Визначити перший потенціал збудження цього атома.
16.4. Енергія іонізації водневого атома 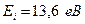. Визначити енергію фотона, що відповідав першій лінії серії Бальмера.
16.5. Визначити довжину хвилі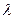 
в серіях Лаймана, Бальмера, Пашена та довжину хвилі 
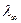- границі цих серій в атомі водню. Потенціал іонізації атома водню .
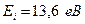16.6. Визначити, яка кількість ліній серії Бальмера, шо випромінює атом водню, потрапляє у видиму область спектра.
16.7. Визначити довжину хвиль в спектрі атома водню, якщо його перевести з основного стану в стан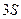 
.
16.8. Енергія валентного електрона в основному стані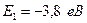 
. Визначити потенціал іонізації атома.
16.9. Яку швидкість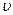 
набуває атом водню при випромінюванні фотона, що відповідає головній лінії серії Лаймана, Бальмера?
16.10. Вільний атом натрію випромінює протон. Визначити зміну довжини хвилі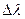 
фотона, що виникає за рахунок віддачі атома при випромінюванні.
16.11. Яку найменшу енергію (в електронвольтах) повинні мати електрони, щоб при збудженні атомів водню ударами цих електронів появились усі лінії всіх серій спектра водню? Яку найменшу швидкість повинні мати ці електрони?
16.12. У яких межах повинна лежати енергія електронів, що бомбардують атом водню, щоб спектр атома водню складався, тільки з однієї лінії?
16.13. В яких межах повинні лежати довжини хвиль монохроматичного світла, щоб при збудженні атомів водню квантами цього світла спостерігали три спектральні лінії ?
16.14. На скільки змінилась кінетична енергія електрона в атомі водню при випромінюванні атомом фотона з довжиною хвилі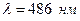 
?
16.15. Визначити потенціал збудження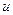 
двократно іонізованого літію.
16.16. Визначити потенціал іонізації однократно іонізованого літію.
16.17. На яку відстань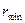 
може наблизитись до нерухомого ядра атома золота 
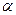- частинка при центральному співударі, якщо її початкова швидкість 
?
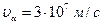16.18. Визначити значення прицільного параметра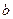 
у випадку розсіювання 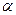-частинки на кут 
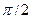ядром атома срібла. Швидкість 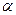- частинки 
.
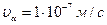16.19. Написати формулу Резерфорда для розсіювання протонів речовиною з атомним номером .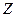
16.20. Визначити: а) радіуси трьох перших борівських орбіт електронів в атомі водню; б) швидкості електронів на них.
16.21. Знайти кінетичну, потенціальну та повну енергію електрона атома водню на першій борівській орбіті.
16.22. Визначити кінетичну енергію електрона, що знаходиться на n - й орбіті в атомі водню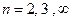 
.
16.23. Знайти: 1) період обертання електрона на першій борівській орбіті атома водню; 2) його кутову швидкість.
16.24. Наскільки (в молях вихідної маси) зменшиться маса атома водню при переході зі стану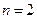 
в основний стан?
16.25. Яке квантове число 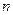відповідає борівській орбіті збудженого атома водню, якщо б радіус орбіти становив 1 мм ? Визначити енергію електрона на цій орбіті.
16.26. Визначити довжину хвилі протона, що відповідає переходу електрона з другої борівської орбіти на першу в однократно іонізованому атомі гелію.
16.27. Вирішити попередню задачу для двократно іонізованого атома літію.
16.28. Електрон, що пройшов через прискорюючу різницю потенціалів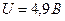 
, зіткнувся з атомом ртуті і перевів його з основного в перший збуджений стан. Яку довжину хвилі буде мати фотон при переході атома ртуті в нормальний стан?
16.29. До електродів рентгенівської трубки прикладена різниця потенціалів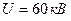 
. Найменша довжина хвилі рентгенівських променів, одержаних від цієї трубки 
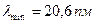. Визначити сталу Планка.
16.30. Визначити короткохвильову границю неперервного рентгенівського спектра, якщо до рентгенівської трубки прикладена напруга: 1) 30 кВ; 2) 40 кВ; 3) 50 кВ.
16.31. Визначити короткохвильову границю неперервного рентгенівського спектра, якщо зменшення прикладеної до трубки напруги на 23 кВ збільшує довжину хвилі в 2 рази.
16.32. Яку найменшу напругу треба прикласти де рентгенівської трубки, щоб одержати всі лінії К - серії, якщо анодом служить: 1) мідь; 2) срібло; 3) вольфрам; 4) платина?
16.33. Визначити найбільшу довжину хвилі К - серії рентгенівських променів для анодів: 1) з заліза; 2) з міді; 3) молібдену; 4) зі срібла. Для К - серії стала екранування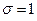 
.
16.34. Визначити постійну екранування 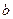для L - серії рентгенівських променів, якщо при переході електрона в атомі вольфраму з 
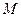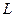на шар випромінюються рентгенівські промені з довжиною хвилі 
.
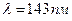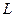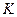16.35. При переході електрона в атомі з на шар випромінюються рентгенівські промені з довжиною хвилі 
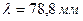. Який це атом?
16.36. Яка мінімальна довжина хвилі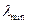 
рентгенівського випромінювання, що випромінюють електрони, які бомбардують екран телевізора з робочою напругою 30 кВ? Чому дорівнює максимальна довжина хвилі?
16.37. Повітря в деякому об’ємі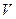 
опромінюється рентгенівськими променями. Доза опромінення 4,5 Р. Визначити, яка доля атомів буде іонізована цим випромінюванням.
16.38. Рентгенівська трубка створює на деякій відстані потужність дози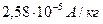 
. Яке число пар іонів у 1 с створює ця трубка в 1 г повітря на цій відстані?
16.39. Визначити для алюмінію товщину шару половинного ослаблення для рентгенівських променів деякої довжини хвилі, якщо відомо, що масовий коефіцієнт поглинання алюмінію для цієї хвилі дорівнює 5,3 м2/кг.
16.40. У скільки разів зменшиться інтенсивність рентгенівських променів з довжиною хвилі 20 пм, при проходженні через шар заліза товщиною 0,15 мм ? Масовий коефіцієнт поглинання заліза для цієї довжини хвилі дорівнює 1,1 м2/кг.
16.41. Визначити товщину шару половинного ослаблення для заліза в умовах попередньої задачі.
16.42. Скільки шарів половинного ослаблення необхідно для зменшення інтенсивності рентгенівських променів у 80 разів.
16.43. При напрузі 16 кВ мінімальна довжина хвилі суцільного рентгенівського спектра становить 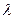= 0,776 А. Обчислити за цими даними сталу Планка.
16.44. Довжина хвилі лінії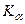 
для ванадію ( 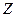= 23) дорівнює 0,25 нм, а для міді ( 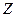= 29) – 0,15 нм. Користуючись цими даними обчислити константи 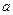і 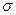у законі Мозлі: 
.
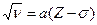16.45. Визначити атомний номер 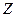елемента, в якого довжина хвилі для лінії 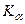дорівнює 0,19 нм. Що це за елемент ?
16.46. Довжина хвилі рентгенівського випромінювання для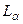 
лінії для заліза ( 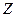= 26) дорівнює 1,76 нм, а для цинку ( 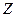= 30) – 1,23 нм. Виходячи із цих даних знайти значення констант 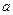і 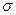в законі Мозлі: .
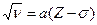17. Елементи квантової механіки
· Довжина хвилі де Бройля:
,
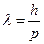де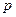 
– імпульс 
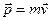– для нерелятивістської мікрочастинки і 
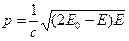–для релятивістської. В останньому випадку 
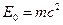– енергія спокою часинки, а 
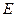– її кінетична енергія.
· Співвідношення невизначеностей Гейзенберга:
, 
, 
;
.
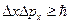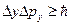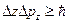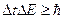· Хвильова функція вільної частинки (одновиміринй випадок):
.
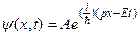· Частинка у нескінченно глибокій потенціальній ямі.
Хвильова функція частинки:
,
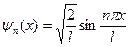де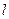 
– ширина ями.
· Енергії рівнів:
,
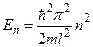де 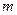– маса частинки.
· Енергія одномірного квантового осцилятора:
.
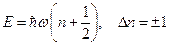· Момент імпульсу електрона.
Повний момент імпульсу електрона із орбітальним квантовим числом :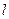
,
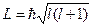де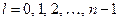 
.
Проекція моменту імпульсу на вісь :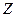
,
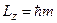де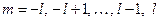 
– магнітне квантове число.
Гіромагнітне співвідношення:
,
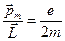де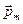 
– орбітальний момент електрона.
· Спіновий момент імпульсу електрона.
Повний спіновий момент імпульсу:
.
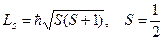Його проекція на вісь :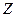
,
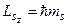де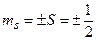 
– спінове квантове число.
· Послідовність електронних оболонок атома у порядку зростання енергії:
.
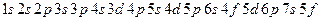· Енергетичні рівні коливального руху молекули:
,
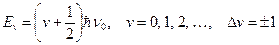де 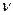– коливне квантове число; 
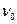– власна частота коливань ядер.
· Енергетичні рівні обертального руху молекули:
,
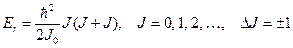де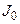 
– момент інерції молекули; 
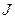– обертальне квантове число.
· Частоти обертальної смуги:
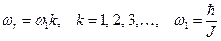
· Частоти обертально-коливальної смуги:
.
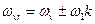· Відношення заселеностей енергетичний рівнів:
.
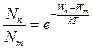17.1. Знайти довжину хвилі де Бройля для електронів, що мають енергію 1,00 еВ та 1,00 кеВ. Електрони вважати нерелятивістськими частинками.
17.2. Знайти довжину хвилі де Бройля для протонів, що мають енергію 1,00 еВ та 1,00 кеВ.
17.3. Знайти довжину хвилі де Бройля для молекули кисню, що рухається із середньою квадратичною швидкістю при температурі 300 К.
17.4. Обчислити довжину хвилі де Бройля для кулі масою 10 г, що рухається зі швидкістю 400 м/с.
17.5. Обчислити довжину хвилі де Бройля для електрона і протона, що мають енергію 1,00 МеВ.
17.6. Кінетична енергія електрона дорівнює енергії спокою. Обчислити довжину хвилі де Бройля для такого електрона.
17.7. Знайти довжину хвилі де Бройля для 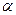- частинки, що рухається по колу радіуса 10,0 мм в магнітному полі з індукцією 2,00 мТл.
17.8. Паралельний пучок електронів, що пройшли прискорюючу різницю потенціалів 30,0 В, падає на діафрагму із двома вузькими щілинами, відстань між якими 50,0 мкм. Знайти відстань між сусідніми максимумами дифракційної картини на екрані, якщо він віддалений на 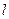= 100 см від щілини.
17.9. Прискорююча напруга в електронному мікроскопі становить 50 кВ. Значення числової апертури дорівнює 0,1. Якої величини роздільну здатність можна очікувати за допомогою цього мікроскопа.
17.10. Вузький пучок моноенергетичних електронів із енергією 26,0 еВ падає на природну грань монокристала під кутом ковзання, що дорівнює 30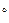 
, при цьому спостерігається максимальна інтенсивність електронного пучка при куті відбивання 30 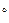. Знайти міжплощинну відстань для цього кристала.
17.11. Показати, що правило квантування орбіт атома водню в теорії Бора одержується з вимоги, щоб на коловій орбіті електрона вкладалось ціле число довжин хвиль де Бройля.
17.12. Використовуючи співвідношення невизначеностей Гейзенберга оцінити величину невизначеності швидкості електрона в атомі водню, приймаючи його розмір за 0,10 нм.
17.13. Оцінити за допомогою співвідношення невизначеностей мінімально можливу енергію електрона в атомі водню і відповідну ефективну відстань його від ядра.
17.14. Оцінити за допомогою співвідношення невизначеностей мінімальну кінетичну енергію електрона, локалізованого в області розміром 0,10 нм.
17.15. Частинка масою 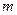рухається в одномірному потенціальному полі, енергія якого описується співвідношенням 
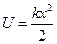(гармонічний осцилятор). Оцінити за допомогою співвідношення невизначеностей мінімально можливу енергію частинки в такому полі.
17.16. Середній час життя атома у збудженому стані становить t = 10-8 с. При переході атома в основний стан випромінюється фотон із довжиною хвилі l = 600 нм. Оцінити природну ширину спектральної лінії на основі співвідношення невизначеностей для енергії та часу.
17.17. Частинка перебуває в основному стані в одномірній потенціальній ямі із нескінченно високими стінками і шириною 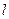. Обчислити ймовірність перебування частинки у першій половині потенціальної ями, тобто у проміжку 
.
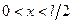17.18. Обчислити густину станів (кількість енергетичних рівнів у одиничному інтервалі енергій) для електрона у нескінченно глибокій потенціальній ямі як функцію енергії і знайти значення цієї густини для 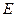= 1,0 еВ, якщо ширина ями становить 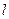= 1,00 мм.
17.19. Хвильова функція мікрочастинки має вигляд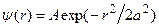 
, де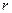 
– відстань від силового центра, 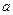– константа. Знайти: а) значення коефіцієнта 
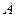; б) найбільш імовірну 
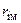та середню 
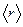відстані частинки від центра.
17.20. Радіальна функція водневоподібного атома має вигляд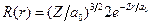 
, де 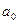– радіус першої борівської орбіти; 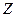– порядковий номер атома. Знайти середнє значення відстані електрона від ядра та середнє значення потенціальної енергії.
17.21. На підставі уявлень класичної фізики електрон можна уявити як заряджену кульку радіуса 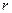з потенціалом 
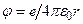. Прирівнюючи потенціальну енергію класичного електрона до його енергії спокою можна знайти “класичний радіус” електрона. Обчислити лінійну швидкість точки на “екваторі” електрона за умови, що момент імпульсу електрона визначається квантово-механічною формулою 
.
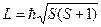17.22. Написати електронну конфігурацію атома калію.
17.23. Написати набори квантових чисел для електронних станів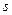 
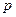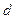, , оболонок.
17.24. Обчислити моменти імпульсу та магнітні моменти для електрона в 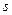, , 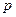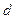станах.
17.25. Визначити кутову швидкість молекули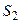 
, що перебуває на першому збудженому обертальному рівні, якщо відстань між її ядрами 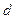= 189 пм.
17.26. Визначити момент імпульсу молекули кисню на другому збудженому обертальному рівні. Відстань між ядрами атомів 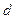= 121 пм.
17.27. Посередині коливально-обертальної смуги спектру випромінювання молекули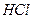 
, де відсутня “нульова” лінія, заборонена правилами відбору, інтервал між сусідніми лініями становить 
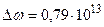рад/с. Обчислити відстань між ядрами молекули.
17.28. Знайти відношення заселеностей енергетичних рівнів оптично активної речовини лазера при температурі 27 оС, якщо при збудженні випромінюється світло із довжиною хвилі 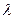= 6943 Å.