Высшей, средней и низшей категорий
Простой формой кристалла называется многогранник, все грани которого можно получить из одной, действуя на нее с помощью операций симметрии, присущих данному классу. Все грани идеальной простой формы кристаллографически равны, имеют одинаковую скорость роста и обладают одинаковыми физическими свойствами. Каждый класс симметрии характеризуется соответствующими ему простыми формами. Простые формы делятся на общие и частичные, открытые и закрытые. Частичная простая форма получается, если исходная грань располагается параллельно или перпендикулярно к осям или плоскостям симметрии, или пересекает их под одинаковыми углами.
Общая простая форма получается, если исходная грань задана в общем положении, то есть на элементах симметрии.
В каждом классе симметрии может быть одна общая и несколько частичных форм. Одна и та же простая форма может встретиться в нескольких классах симметрии. Закрытыеформы полностью замыкают пространство и могут существовать самостоятельно. Открытые формы не замыкают пространство и существуют лишь в комбинациях с другими простыми формами. Всего существует 47 простых форм.
Для кристаллов низшей и средней категорий возможные 22 простые формы.
В триклинной сингонии существуют лишь две простых формы: Моноэдр - форма, которая состоит из одной грани (рис. 14а), пинакоид - состоит из двух параллельных граней (рис.14б).
В моноклинний сингонии к этих двум формам прибавляются: диедр - состоит из двух граней, которые пересекаются (рис.14 в,г), ромбическая призма - это призма, сечении которой представляет собой ромб (рис.14 д).
В ромбической сингонии прибавляются: ромбическая пирамида и дипирамида (рис.14е,ж,с), сечение которых представляет собой ромб, ромбический тетраэдр (рис.14е) - закрытый четырехгранник, грани которого представляют собой косоугольные треугольники. В средних сингониях кроме моноэдра и пинакоида существуют призмы, пирамиды и дипирамиды (рис.15). Они отличаются сингониями в зависимости от порядка оси и формой пересечения, перпендикулярной к главной оси. Тригональные призмы, пирамиды имеют в сечении треугольник, тетрагональные - квадрат, гексагональные - шестиугольник.
У призм грани пересекаются ребрами, которые параллельны главной оси, у пирамид - ребрами, которые сходятся в одной точке на главной оси, в дипирамидах - в двух точках на главной оси, причем нижние грани расположены точно под верхними. Призмы и пирамиды являются открытыми формами, они могут существовать только в комбинациях. Дипирамида - закрытая форма. В классах симметрии, в которых существуют плоскости, проходящие вдоль главной оси, возможны также призмы, пирамиды и дипирамиды, каждая грань которых удвоенная. Сечения таких простых форм, перпендикулярных к главной оси, представляют собой дитригон, дитетрагон и дигексагон (рис.15) Углы у них – равные, через один.
Только в тригональной сингонии (единой из всех сингоний) есть закрытая форма - ромбоэдр. (рис.16). Все шесть его граней представляют собой ромбы. Нижняя грань ромбоэдра расположена симметрично относительно двух верхних.
В тетрагональной сингонии есть тетрагональный тетраэдр, составленный с четырех граней в виде равнобедренных треугольников

а б в г

д е ж с
Рис. 14 - Простые формы кристаллов низшей категории;
а - моноэдр, б - пинакоид, в – диэдр плоскостной, г - диэдр осевой,
д - ромбическая призма, е - ромбический тетраэдр,
ж - ромбическая пирамида, с – ромбическая дипирамида.
В средних сингониях существуют также трапецоэдры и скаленоэдры, но изучение их не предусмотрено программой.
При определении числа и вида простых форм в кристаллическом многограннике следует после определения вида симметрии найти число сортов граней, из которых состоит данный многогранник. Разные грани всегда принадлежат к разным простым формам. Число простых форм в многограннике не может быть меньше, чем число сортов граней.




Рис. 15 - Призмы, пирамиды и дипирамиды: а – тригональные; б – дитригональные; в – тетрагональные; г – дитетрагональные; д – гексагональные; е – дигексагональные.

Рис. 16-ромбоэдр
Для удобства определения простых форм в комбинациях можно пользоваться табл. 3.
Таблица 3 - Простые формы низших и средних категорий
| Сингония | Название простой формы | Число граней | Расположение граней | Поперечное сечение перерези | |||
| Низшая категория | |||||||
| Триклинная | Моноэдр | ||||||
| Пинакоид | Грани параллельны | ||||||
| Моноклиннная | Моноэдр | ||||||
| Пинакоид | Граны параллельны | ||||||
| Диэдр | Грани пересекаются | ||||||
| Ромбическая призма | Грани попарно параллельны | Ромб | |||||
| Ромбическая | Моноэдр | ||||||
| Пинакоид | Грани параллельны | ||||||
| Диэдр | Грани пересекаются | ||||||
| Ромбическая призма | Грани попарно параллельны | Ромб | |||||
| Ромбическаяпирамида | Грани пересекаются в одной точке | Ромб | |||||
| Ромбическаядипирамида | Грани пересекаются в двух точках | Ромб | |||||
| Средняя категория | |||||||
| Тригональная | Моноэдр | ||||||
| Пинакоид | Грани перпендикулярные главный оси | ||||||
| Тригональна призма | Грани параллельны главный оси | Треугольник | |||||
| Дитригональна призма | Грани параллельны главный оси | Дитригон | |||||
| Тригональна пирамида | Грани пересекают главную ось в одной точке | Тригон | |||||
| Дитригональна пирамида | Грани пересекают главную ось в одной точке | Дитригон | |||||
| Тригональна дипирамида | Грани пересекают главную ось в двух точках | Треугольник | |||||
| Дитригональна дипирамида | Нижние грани расположены под верхними | Дитригон | |||||
| Ромбоедр | Грани пересекают главную ось в двух точках, нижняя грань расположена симметрично между двумя верхними | ||||||
| Тетрагональная | Тетрагональная призма | Грани параллельны главной оси | Квадрат | ||||
| Дитетрагональная призма | Грани параллельны главной оси | Дитетрагон | |||||
| Тетрагональная пирамида | Грани пересекают главную ось в одной точке | Тетрагон | |||||
| Тетрагональная дипирамида | Грани пересекают главную ось в двух точках, нижние грани расположены под верхними | Тетрагон | |||||
| Дитетрагональная дипирамида | Грани пересекают главную ось в двух точках, нижние грани расположены под верхними | Дитетрагон | |||||
| Гексагональная | Гексагональная призма | Грани параллельны главной оси | Шестиугольник (гексагон) | ||||
| Дигексагональная призма | Грани параллельны главной оси | Дигексагон | |||||
| Гексагональная пирамида | Грани пересекают главную ось в одной точке | гексагон | |||||
| Дигексагональная пирамида | Грани пересекают главную ось в одной точке | дигексагон | |||||
| Гексагональная дипирамида | Грани пересекают главную ось в двух точках, нижние грани расположены под верхними | гексагон | |||||
| Дигексагональна дипирамида | Грани пересекают главную ось в двух точках, нижние грани расположены под верхними | дигексагон | |||||
В кристаллах кубической сингонии нет простых форм, характерных для низших и средних сингоний. Всего в кубической сингонии - 15 новых простых форм, некоторые из них приведены на (рис.19). Все они закрытые, здесь присутствуют замкнутые и открытые простые формы.
К открытым простым формам относятся многогранники, приведенные в табл.4.
Кубический тетраэдр - четырехгранник состоит из четырех равносторонних треугольников, гексаэдр – имеет шесть граней в виде квадратов, октаэдр - восемь граней в виде правильных треугольников, пентагон додекаэдр – двенадцать граней в форме пятиугольников, ромбододекаэдр - двенадцать граней в форме ромбов (рис. 19).


тетраэдр куб октаэдр ромбический додекаэдр



пентагондодекаэдр тригонтритетраэдр тетригонтритетраэдр пентагонтритетраэдр




тетрагексаэдр тетрагонтриоктаэдр тригонтриоктаэдр гексатетраэдр
Рис. 19 - Простые формы кубической сингонии
"Надстраивая" на гранях тетраэдра три треугольника, четырехугольника, пятиугольника, получаем тригонтритетраэдр, тетрагонтритетраэдр и пентагонтритетраэдр. Если же на каждой грани тетраэдра "надстроить" по шесть треугольников, получим гексатетраэдр. Он имеет 24 грани.
Таблица 4 - Простые формы кубической сингонии
| Название простой формы | Число одинаковых граней | Символы граней |
| Тетраэдр Производные от тетраэдра Гексатетраэдр | ||
| Гексаэдр Тетрагексаэдр | ||
| Октаэдр Производные от Октаэдра Гексаоктаэдр | ||
| Додекаэдр Дидодекаэдр |
Аналогично, из октаэдра выходят тригонтриоктаэдр (по три треугольника на каждой грани), тетрагонтриоктаэдр (по три четырехугольника на каждой грани), пентагонтриоктаэдр (по три пятиугольника на каждой грани) и 48-гранник - гексаоктаэдр (по шесть треугольников на каждой грани). "Надстраивая" на гранях гексаэдра (куба четыре треугольника) - (четырехэтажная крыша), получаем пирамидальный куб или тетрагексаэдр (рис. 19).
Удваивая число граней пентагондодекаэдра, получаем дидодекаэдр. Некоторые из простых форм кубической сингонии определяются просто по числу граней. Это тетраэдр (четыре грани), гексаэдр (шесть граней), октаэдр (восемь граней), гексаоктаэдр (48 граней). Другие простые формы в комбинациях можно отличить, учитывая число граней и их символы (табл.4). При этом грани гексаэдра всегда имеют символ {100}, тетраэдра и октаэдра и их производных - {111}, а грани ромбододекаэдра и пентагондодекаэдра - {110} Символы простых форм берут в фигурные скобки.
Порядок выполнения работы:
1. Внимательно изучить рисунки многогранников (см. Приложения);
2. Определить элементы и формулу симметрии;
3. Определить сингонию и класс;
4. Определить число сортов граней (для кубической сингонии – число граней одинакового сорта);
5. Определить координатные оси (установка кристалла) и символы граней одного сорта (для кубической сингонии);
6. Определить простые формы.
Пример 1. Модель берилла – Аl2 Ве2 [Si6 О18] (рис.20). Формула симметрии L66L27РС. Сингония -гексагональная, класс планаксиальный. Число сортов одинаковых граней – четыре. Две грани одинаковые (1), параллельные между собой и перпендикулярны главной оси L6, - пинакоид. Шесть одинаковых граней (2), параллельных главной оси, - гексагональная призма. Двенадцать одинаковых граней (3), которые при их продолжении пересекают главную ось L6 в двух точках, гексагональная дипирамида. Двенадцать одинаковых граней (4), аналогично граням (3), образуют гексагональную дипирамиду. Таким образом, модель представляет собой комбинацию гексагональной призмы, двух гексагональних дипирамид и пинакоида.

Рис. 20. Модель берилла
Пример 2. Модель (рис. 21). Формула симметрии ЗL4 4L36L2 9РС. Сингония кубическая, класс планаксиальний. Число сортов одинаковых граней - три. Грани (1): число граней - 6, символ {100} - простая форма – гексаэдр. Грани(2): число граней - 8. символ {111} - простая форма - октаэдр. Грани (3): число граней - 12. Такое количество граней отвечает или одному из тритетраэдров или додекаэдру. Определяем символ граней {110} - такой символ отвечает ромбическому додекаэдру. И так, - это ромбический додекаэдр.
Модель представляет собой комбинацию гексаэдра, октаэдра и ромбододекаэдра.

Рис. 21. Комбинация простых форм кубической сингонии
Варианты исходных данных для выполнения практического задания приведены в приложении.
ПРАКТИЧЕСКАЯ РАБОТА №5
КРИСТАЛЛИЧЕСКАЯ РЕШЕТКА
Кристаллической решеткой называется бесконечное векториальное построение, в котором атомы или ионы занимают определенное геометрическое положение. Кристаллическая решетка строится на трех основных не компланарных трансляциях, параметрах решетки а, в, с. Кристаллические решетки характеризуются элементарным параллелепипедом - наименьшим объемом, выражая закономерность расположения атомов или ионов в пространстве.
Элементарный параллелепипед должен отвечать следующим условиям:
1. Симметрия всей кристаллической решетки должна быть одинаковой;
2. Число прямых или равных углов и равных ребер должно быть максимальным;
3. Элементарная ячейка должна иметь минимальный объем.
Иногда удобно выбирать элементарную ячейку в которой, кроме узлов в вершинах, имеются и другие узлы. Для примера рассмотрим как лучше выбрать плоскую элементарную решетку в плоской сетке, изображенной на рис. 22.
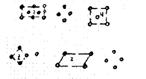
Рис. 22 - Выбор элементарной ячейки
Ячейка 3 наименьшая по площади, но не отвечает симметрии решетки; ячейка 2 отвечает симметрии, но у нее нет прямых углов; ячейка 1 отвечает симметрии, углы у нее прямые, но она не отвечает условию минимума площади. Только ячейка 4 целиком характеризует данную плоскую сетку.
Еще в середине XIX столетия, когда микроструктура веществ была неизвестна, Бравэ, исходя из идеи о периодическом размещении центров тяжести сферических частиц, показал, что все многообразие кристаллических структур можно описать с помощью 14 типов решеток, которые подразделяются на 7 кристаллографических сингоний. По расположению узлов решетки разбиваются на четыре типа: примитивные (Р), в которых узлы решеток располагаются только в вершинах; объемноцентрированные (J) - имеют дополнительный узел в центре решетки; гранецентрированные (F) - дополнительные узлы по одному в центре каждой грани; базоцентрированные (С, А, B) - дополнительные узлы в центре двух противоположных граней (рис. 23).
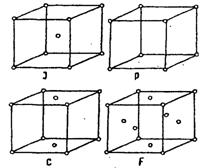
Рис. 23. Примитивная (Р), объемноцентрированная (J),
гранецентриррованная (F) и базоцентрированная (С) решетки
Только в ромбической сингонии есть все четыре типа элементарных параллелепипедов. В тригональной, гексагональной и триклинной - только примитивные; в моноклинной - примитивная и базоцентрованная; в кубической - примитивная, объемноцентрированная и гранецентрированная, в тетрагональной - примитивная и объемноцентрированная (табл.5). Следует помнить, что кристаллические решетки имеют бесконечное строение, поэтому узел, который находится в вершине кристаллических решеток, принадлежит одновременно восьми элементарным ячейкам, и на одну ячейку приходится 1/8 узла (атома, иона, группы, табл.5). Итак, на одну примитивную ячейку приходится 1/8 х 8=1 (атом).
На одну объемноцентрированную решетки приходится 1/8х8+1=2 (атома); на одну гранецентрированную решетку - 1/8х8+1 2х6 = 4 (атома); на одну базоцентрированную решетку - 1/8х 8+1/2х2 = 2 (атома).
Ребра элементарных ячеек принимаются за кристаллографические оси. Трансляция по Х обозначается а, по Y - в, по Z – с.
Трансляция обязательно берется между двумя одинаковыми узлами. Так, например, в решетках NaCl чередуются атомы Nа и Сl. Однако элементарная трансляция будет равняться расстоянию Nа - Cl ли Сl-Сl. Один из узлов кристаллических решеток принимаем за начало системы координат (рис. 24). Координаты этого узла будут [000], координаты узлов на вершинах объємноцентрированной решетки:
[111], [101], [011], [101], [001], [110], [100], а координаты узла, который находится в центре решетки, - 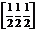 .
.
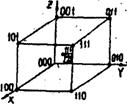
Рис. 24. Координаты узлов объємноцентрированной решетки
Таблица 5
Тип решеток Бравэ
| Сингония | Тип решетки | |||
| Примитивная | Базоцентрированная | Объемноцентрированная | Гранецинтрированная | |
| Триклинная |  Р Р | |||
| Моноклинная |  Р Р |  | ||
| Ромбическая |  С С | 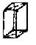 С С | 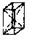 I I | 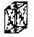 F F |
| Тригональная |  Р Р | |||
| Тетрагональная | 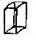 P P |  I I | ||
| Гексогональная |  P P |  I I |  F F | |
| Кубическая |  P P |
Для определения плоскостей, которые можно провести в элементарных ячейках пространственных решеток (следовательно, и в самих пространственных решетках), а также для определения кристаллографических направлений в кристаллографии принята система индексации. По этой системе для кубической решетки индексация плоскостей осуществляется тремя цифрами, заключенными в круглые скобки. Эти цифры представляют собой три взаимно простых целых числа, пропорциональных обратной величине отрезков, отсекаемых плоскостью на координатных осях, причем за единицу измерения отрезков принимают параметр решетки. На рис. 25 даны обозначения некоторых плоскостей кубической элементарной ячейки.
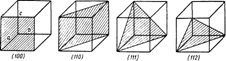
Рис. 25 Индексация плоскостей в кубической решетке
В гексагональной элементарной ячейке индексацию плоскостей производят по обратным величинам отрезков, отсекаемых рассматриваемой плоскостью на четырех кристаллографических осях (рис. 26), три из которых а1,а2 и а3 лежат в плоскости основания шестигранной призмы (в так называемой плоскости базиса), а четвертая с совпадает с осью призмы. На рис. 26 указаны также обозначения некоторых плоскостей в гексагональной ячейке. Знак минус над цифрой показывает, что плоскость отсекает отрезок на отрицательном направлении оси. Заметим, что обозначение отдельных плоскостей в элементарных ячейках кристаллографической решетки сохраняют одинаковым для всех плоскостей, проведенных в пространственной решетке, параллельных данной рассматриваемой плоскости.
В пространственной решетке рассматривают также кристаллографические направления. В качестве прямой, определяющей направление какого-либо семейства параллельных прямых, обычно выбирают прямую, проходящую через начало координат. Вдоль этой прямой расположен ряд атомов, отстоящих один от другого на определенном. расстоянии. Положение этой прямой в пространстве определится координатами любого атома, на ней расположенного. Поэтому в. качестве индексов направления берут три взаимно простых целых числа, пропорциональных координатам любого атома, лежащего на рассматриваемой прямой, причем за единицу измерения принимается параметр решетки (индексы направлений заключаются в квадратные скобки). На рис. 27 дано схематическое изображение основных направлений в кубической элементарной ячейке и их обозначение.
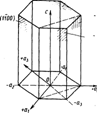
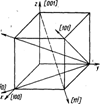
Рис. 26 Индексация плоскостей Рис. 27 Индексация направлений
в гексагональной решетке в кубической решетке
Порядок выполнения работы:
1. Внимательно изучить полученные типы кристаллических решеток;
2. Выделить элементарную ячейку в кристаллической решетки;
3. Определить тип решетки Бравэ;
4. Определить координаты узлов;
5. Определить количество атомов каждого рода, которые приходятся на элементарную ячейку, вычислить число формульных единиц, которые входят в ячейку.
КРИСТАЛЛОХИМИЯ
ПРАКТИЧЕСКАЯ РАБОТА №6
