Выбор кристаллографических осей

И УСТАНОВКА КРИСТАЛЛОВ.

СИМВОЛЫ ГРАНЕЙ

Трехмерная система координат в кристаллографии выбирается соответственно симметрии кристалла. В общем случае - это косоугольные координаты с разными масштабными отрезками по осям, которые дают возможность описать любую грань тремя простыми целыми числами.

В кристаллографии используется правая система координат. Оси координат выбираются по осям симметрии или по нормалям к плоскостям симметрии, а если их нет - по ребрам кристаллического многогранника.

Для каждой сингонии являются установленные правила выбора кристаллографических осей (рис.7).

Отрезок, который отсекается гранью по оси Х обозначается а, по оси Y - b , по оси Z - с. Угол между осями Z и Y - a, между Х и Z - b, между Х и Y - g.

Каждую сингонию можно характеризовать элементарным параллелепипедом с сторонами а,b,с и углами между нимиa, b, g.

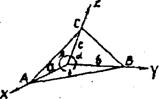
Рис.7 Геометрические константы кристалла.

В триклинной сингонии оси координат выбирают по трем непараллельным одного другому ребрам кристалла, при этом ось Z-вдоль наибольшего ребра кристалла, с>а>b. Углы между кристаллографическими осями должны по возможности приближаться к прямым (b< 90° ).

Элементарный параллелепипед косоугольный.

В моноклинной сингонии ось Y выбирается вдоль оси L₂, нормально к плоскости Р, Х и Z - к плоскости, перпендикулярной к Y. Углы между кристаллографическими осями: a=g=90°; b>90. Элементарная ячейка - прямая призма с параллелограммом в основе.

В ромбической сингонии система координат прямоугольная. Оси координат выбираются вдоль L₂ или по нормали к Р. Обязательным условием является: с>а>b; a=b=g=90⁰. В случае L₂ 2Г ось Z выбирается вдоль L₂, Х и Y - по нормалям к Р Элементарная ячейка – параллелепипед.

В тетрагональной сингонии ось Z выбирается вдоль L₄, оси Х и Y - вдоль L₂ или нормально к Р в плоскости, перпендикулярной Z. Отрезки по Х и Y одинаковые. Элементарная ячейка - призма с квадратом в основе.

В кубической сингонии оси координат выбираются вдоль осей L₄, а если их нет – вдоль L₂.

Элементарный параллелепипед - куб.

Формы элементарных параллелепипедов всех сингонии показаны на рис. 8.

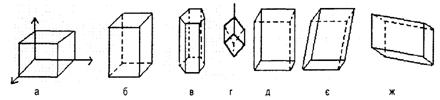
Рис.8 - Элементарные параллелепипеды разных сингоний:

а - кубическая; б - тетрагональная; в - гексагональная; г - тригональная; д - ромбическая; с - моноклинная; ж - триклинная

Для тригональной и гексагональной сингоний более удобным является введение дополнительной координатной оси Y.

Здесь ось Z выбирается вдоль L₃ или L₆. В плоскости, перпендикулярной к оси Z, располагаются три координатные оси X, Y и Y’ (по L₂ или нормалям к Р), углы между этими осями составляют 120° Элементарная ячейка в гексагональной сингонии - прямоугольная призма с ромбом в основе Три таких ячейки составляют гексагональную призму. В тригональной сингонии элементарная ячейка - ромбоэдр (сжатый или растянутый вдоль одной из пространственных диагоналей куб) а=b=с, a=b=g¹90 ⁰.

Кристаллографические системы координат всех сингоний изображены на рис. 9.

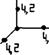
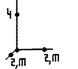
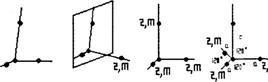
Рис. 9. Кристаллографические системы координат разных сингоний

Кристаллографические системы координат дают возможность охарактеризовать взаимное расположение граней. Для этого некоторую грань, которая пересекает все три оси, принимают за единичную (масштабную). Отрезки, которые отсекаются этой гранью на осях, является единицей или масштабом для данных осей.

Пусть задана некоторая грань АВС и масштабная грань А₁ В₁ С₁.

Тогда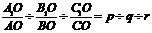

Однако в кристаллографии для числовой характеристики грани применяются не числа p, q, r, а обратные им величины. Сведя к общему знаменателю и отбросив его, получаем три целых числа h, k, l, названные символами граней (индексами Миллера). Символы граней записываются в круглых скобках без знаков препинания между ними (рис.10): .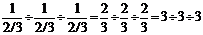

Символ грани АВС – (ЗЗЗ). Для простоты будем применять только индексы (111), независимо от расположения грани относительно единичной. Если грань параллельная к какой-нибудь кристаллографической оси, то ее символ по этой оси превратится в 0, потому что число, разделенное на ∞ дает 0. Например, грань параллельная оси X, будет иметь символ (011), параллельная оси Y – (101), параллельная оси Z – (110) Если грань пересекает ось в отдаленной части, то над соответствующим символом ставится знак "-".

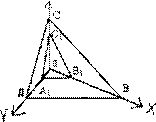
Рис.10. Символы граней

и В

\

На рис. 11 приведены символы граней куба. Передняя и задняя грани имеют символы 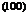и( 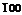), боковые 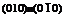, верхняя и нижняя .

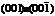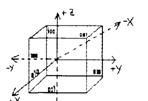
Рис.11. Символы граней куба

Особое внимание следует уделить символам граней тригональных и гексагональных кристаллов. Здесь будет не три, а четыре цифры. Следует учитывать, что дополнительное значение оси Y’ будет в области, направленной от нас, а отрицательное - к нам (рис.12). Грани гексагональной призмы в четырехосной системе координат будут иметь символы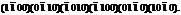

Из приведенных примеров видно, что однотипные грани имеют похожие символы. Так, символ куба можно представить как (100), а символ боковых граней гексагональной призмы - {1100}

Порядок выполнения работы:

1. Внимательно изучить полученные модели многогранников (заданные рисунки);

2. Определить элементы и формулу симметрии;

3. Определить сингонию и класс симметрии;

5. Соответственно правилам данной сингонии выбрать кристаллографическую систему координат;

6. Определить число однотипных граней;

7. Для каждого сорта граней определить их символы, записав их в столбик.

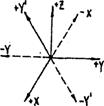
Рис. 12 - Направление осей в гексагональной и тригональной сингониях.

Пример. Модель в виде тетрагональной призмы (рис. 13):

1. Формула симметрии L₄4L₂5РС,

2. Сингония - тетрагональная, класс планаксиальний;

3. В соответствии с правилом установки кристалла ось Z выбираем вдоль L₄, а оси Х и Y - по осям L₂ так, чтобы они проходили через центр граней;

4. В модели есть две разновидности граней - четыре боковых грани, верхняя и нижняя грани;

5. Символы граней: 4 2

(100) (011)

(100)

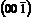
(010)

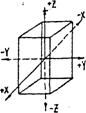
Рис. 13 - Тетрагональная призма

ПРАКТИЧЕСКАЯ РАБОТА №4