Определение сингоний и класса симметрии

Определяя элементы симметрии кристаллических многогранников, Вы, наверное, обратили внимание на то, что разные на внешний вид многогранники имеют одинаковые формулы симметрии. Так, например, тетрагональная призма и тетрагональная дипирамида имеют формулу симметрии L₄4L₂5РС.

Полная совокупность элементов симметрии данной фигуры называется точечной группой симметрии, или классом симметрии. Название "точечная группа" означает, что при всех симметричных преобразованиях хотя бы одна точка в фигуре остается на месте.

А.В. Гадолин определил, что возможны лишь 32 комбинации элементов симметрии, которые образовывают 32 класса симметрии. Их можно вывести, зная теоремы соединения элементов симметрии

Теорема 1. Линия пересечения двух плоскостей симметрии всегда есть осью симметрии с углом поворота вдвое большим, чем угол между плоскостями.

Теорема 2. Точка пересечения парной оси симметрии с перпендикулярной ей плоскостью есть центр симметрии.

Теорема 2а. (обратная) Если на парной оси симметрии есть центр симметрии, то перпендикулярно к этой оси проходит плоскость симметрии

Теорема 2б. (обратная) Если через центр симметрии проходит плоскость симметрии, то перпендикулярно к этой плоскости через центр симметрии проходит парная ось

Теорема 3. Если перпендикулярно к оси симметрии п-го порядка проходит ось 2-го порядка, то таких осей будет n.

Теорема 4. Если вдоль оси симметрии n-го порядка проходит плоскость симметрии, то таких плоскостей будет n.

Теорема 5 (теорема Ейлера) Равнодействующая двух осей симметрии, которые пересекаются, есть третья ось, которая проходит через точку их пересечения.

Теорема 6. Если вдоль парной инверсионной оси проходит плоскость симметрии, то между ними располагаются оси симметрии 2-го порядка.

На основе теорем симметрии можно видеть, что наличие одних элементов симметрии (порождающих) вызовет присутствие других элементов симметрии (порожденных).

Чтобы вывести 32 класса симметрии нужно рассмотреть все возможные соединения элементов симметрии. Для этого в кристаллах, которые имеют единичное направление, выбираем, как исходный элемент симметрии ось симметрии и к ней поочередно прибавляем все другие элементы симметрии (рис.6)

Примитивными классами симметрии называются классы, в которых есть только поворотная ось симметрии (рис.6а): L₁; L₂; L₃; L₄; L₆.

Центральные классы получаются из примитивных добавлением к ним центра симметрии. При этом, если ось симметрии парная, возникает согласно теореме 2 и плоскость симметрии, нормальная к ней (рис.6б).

определение сингоний и класса симметрии - student2.ru

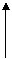
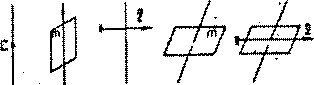
а б в г д е

Рис. 6. Расположение элементов симметрии относительно единичного направления

Порождающая ось: L₁, L₂, L₃; L₄; L_б.

Порожденная плоскость: Р; Р; Р.

Класс симметрии: L₁; L₂PС; L₃С, L₄РС; L₆РС.

Планарные классы получаем, прибавляя к оси симметрии плоскость, которая проходит через нее (рис.6в). На основе теоремы 4 таких плоскостей будет n.

Порождающая ось: L₁; L₂; L₃; L₄; L₆.

Класс симметрии: Р; L₂; 2Г; L₃ ЗР; L₄ 4Г; L₆ 6Г.

Аксиальные классы получаем, прибавляя к оси симметрии ось 2-го порядка, перпендикулярную к порождающей оси (рис. 6г) тогда согласно теореме 3 таких осей будет n.

Порождающая ось: L₁; L₂; L₃; L₄; L₆.

Класс симметрии: L₂; ЗL₂; L₃ 3L₂; L₄4L₂; L₆6L₂

Таким образом, класс L₂ правильнее отнести не к примитивному, а к аксиальному.

Планаксиальные классы получаем, прибавив к порождающей оси 2-го порядка продольные оси 2-го порядка и поперечные плоскости, (рис.6д,е) и учитывая теоремы 2-4.

Порождающая ось: L₁; L₂; L₃; L₄; L₆.

Класс симметрии: L₂PC; 3L₂3PC; L₃3L₂3PC; L₄4L₂5PC; L₆6L₂7PC.

Перечисленными классами исчерпываются соединение элементов симметрии низшей и средней категории с поворотной осью симметрии.

Инверсионно-примитивные классы - это классы, в который есть единая инверсионная ось: L₂; L₄; L₆.

Инверсионно-планарные классы получаются, если к порождающей инверсионной оси прибавить плоскости, которые проходят вдоль нее. При этом возникает два класса: L₄2L₂2P; L₃3L₂4P.

Рассмотрим классы, которые не имеют единичных направлений. К примитивному классу принадлежит многогранник, который имеет только оси симметрии, а именно: 4L₃3L₂.

Если к этому многограннику прибавить центр симметрии, то через появление 3L₂, получим ЗР. Итак, в центральном классе фигура будет иметь формулу 4L₃3L₂ ЗРС.

К аксиальному классу будет относиться фигура 3L₄4L₃6L₂, к планарному – 4L₃3L₂6Г, а к планаксиальному – 3L₄4L₃6L₂9РС.

Классы симметрии объединяются в сингонии.

Сингонией называется группа видов симметрии, которые обладают одним или несколькими подобными элементами симметрии при одинаковом числе единичных направлений.

Единичным направлением в кристалле называется направление, которое не повторяется Так, в трехгранной (тригональной) призме есть одна ось 3-го порядка L₃, в шестигранной (гексагональной) призме - одна ось 6-го порядка L₆.

В кубе нет единичных направлений, так как любое направление повторяется несколько раз. В кристалле, который имеет только центр симметрии, нет симметрично-равных направлений. Все направления здесь единичные.

В кристаллографии различают семь сингоний: триклинную, моноклинную, ромбическую, тригональную, тетрагональную, гексагональную и кубическую.

В табл.2 приведенные элементы симметрии, характерные для всех сингоний.

Таблица 2

Характеристика сингоний

Категории	Сингонии	Число единичных направлений	Характерные элементы их соединения
Низшая Несколько единичных направлений Нет осей порядка выше 2	Триклинная Моноклинная Ромбическая	Все Все Три	С Р; L_2; L₂РС L₂2P; 3L₂ 3L₂ЗРС
Средняя Одно единичное направление, которое совпадает с единой осью порядка выше 2	Тригональная Тетрагональная Гексагональная	Одно Одно Одно	L₃ L₄ L₆
Высшая Нет единичных осей порядка выше 2	Кубическая	Нет	4L₃