Определение элементов симметрии кристаллов

Кристаллической симметрией называется правильная повторяемость элементов ограничения (ребер, граней, углов) и других свойств кристаллов по определенным направлениям. Для выявления повторяемости (закономерности) пользуются вспомогательными геометрическими образами – особыми точками, прямыми, плоскостями, с помощью которых математически характеризуется симметрия фигур. Эти образы называются элементами симметрии.

К ним относятся: центр симметрии, плоскости симметрии, простые и сложные оси симметрии. Для обозначения элементов симметрии в кристаллографии используют условные символы. Наиболее распространенными являются символы, принятые Интернациональным союзом кристаллографов – международная символика и символика формул симметрии (Табл.1)

Таблица 1 - Обозначение элементов симметрии

Название	Обозначение	Изображение по отношению к плоскости рисунка
международная символика	формула симметрии	перпендикулярное	параллельное
Плоскость симметрии	Т	Р	// =
Центр симметрии	И	С	С	○
Поворотная ось.	Г	Lп
Двойная	И	L2	♦	♦-♦
Тройная		Lз	▲	▲-▲
Четвертная		L4	■	■-■
Шестерная		L6	•	·-·

Центром симметрии С (инверсии) кристаллического многогранника называется точка, лежащая внутри кристалла, в диаметрально противоположных направлениях от которой располагаются одинаковые элементы ограничения и другие свойства многогранника. Центр симметрии обозначается буквой С латинского алфавита.

В многограннике, обладающим центром симметрии С, каждой грани отвечает другая грань, равная и параллельная первой.

Убедиться в параллельности двух граней просто: необходимо положить многогранник на стол испытываемой гранью, наверху будет находиться вторая грань параллельная плоскости стола, а следовательно, параллельная и первой грани. Если хотя бы для одной грани не найдена парная ей параллельная грань – центр симметрии отсутствует (рис.1).

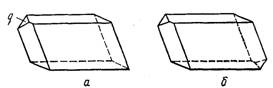
Рис.1 Многогранники

а) без центра симметрии (грань q не имеет параллельной и равной грани);

б) с центром симметрии (все грани попарно параллельны и равны).

Куб и параллелепипед представляют собой простейшие примеры многогранников с центром симметрии. На рис.2 изображена шестигранная пирамида, лишенная центра симметрии

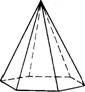
Рис. 2. Шестигранная (гексагональная) пирамида

Чтобы найти центр симметрии необходимо положить многогранник на стол, по очереди каждой гранью и проверить, есть ли на верху такая же грань, расположенная горизонтально. Обе грани верхняя и нижняя могут быть не только параллельными, но и антипараллельными, то есть одинаковыми и расположенными напротив.

Плоскостью симметрии (Р) кристаллического многогранника называется плоскость, по обе стороны которой располагаются одинаковые элементы ограничения и повторяются одинаковые свойства кристалла.

Плоскость симметрии обладает свойством зеркальности: каждая из частей кристалла, рассеченного плоскостью симметрии, совмещается с другой, т.е. является как бы ее зеркальным изображением.

В различных кристаллах можно провести разное количество плоскостей симметрии. Все плоскости симметрии пересекаются в одной точке. Например, в кубе имеется девять плоскостей симметрии: три взаимноперпендикулярных, которые проходят через центры ребер и шесть диагональных (рис. 3).

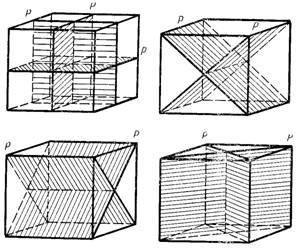
Рис. 3. Плоскости симметрии куба

Плоскость симметрии обозначается заглавной буквой латинского алфавита Р, а коэффициент, стоящий перед ней, показывает количество плоскостей симметрии в многограннике. Таким образом, для куба можно записать – 9Р.

Осью симметрии кристаллического многогранника называется прямая линия, при повороте вокруг которой на некоторый определенный угол, фигура совмещается сама с собой. Порядком оси симметрии n называется количество совмещений кристалла с первоначальным положением при повороте на 360⁰.

В кристаллическом многограннике может быть несколько осей симметрии различных порядков: 1, 2, 3, 4 и 6. Осей 5 и порядка большего 6 – ти не существует. Это ограничение обусловлено тем, что кристаллическое вещество – бесконечная система материальных частиц, симметрично повторяющихся в пространстве. Такие симметричные бесконечные ряды, сетки, решетки, непрерывно заполняющие пространство несовместимы с осями 5,7 и других порядков. Так, в кубе три оси симметрии четвертого порядка (через середины противоположных граней); четыре оси третьего порядка (проводятся через противоположные вершины трехгранных углов) и шесть осей второго порядка (через середины противоположных ребер) (рис. 4).

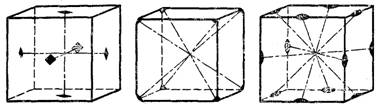
Рис. 4. Оси симметрии в кубе

В кристаллах наряду с обычными осями симметрии выделяют так называемые инверсионные оси.

Инверсионной осью кристалла называется линия, при вращении вокруг которой на некоторый определенный угол и последующим отражением в центральной точке многогранника (как в центре симметрии) совмещаются одинаковые элементы ограничения.

Инверсионная ось представляет собой совместное действие оси вращения и одновременно обращена (инверсии) в центре симметрии.

Инверсионная ось обозначается символом 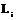. Доказана возможность существования инверсионных осей 1-го, 2-го, 3-го, 4-го и 6-го порядков. Инверсионные оси обозначаются 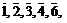или

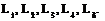
В тригональной призме (рис.5) прямая LL – ось третьего порядка 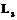. В тоже время она одновременно является инверсионной осью шестого порядка. Так, при повороте на 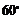вокруг оси любых частей многогранника и последующего отражения их в центральной точке фигура совмещается сама с собой.

Иными словами, поворот ребра АВ этой призмы на вокруг LL приводит его в положение А, В отражение ребра А, В, через центр совмещает его с ДF.

Совокупность элементов симметрии для данного многогранника дает форму симметрии, в которой на первом месте записывается ось симметрии, потом плоскости, а в конце центр симметрии. Никаких знаков разделения между ними не ставиться. Если многогранник не имеет ни каких элементов симметрии, его формула 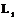. Оси симметрии записываются последовательно от осей высшего порядка до осей низшего порядка.

Например, формула симметрии куба: .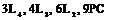

Для обозначения полной совокупности элементов симметрии кристалла полезно знать что существует: 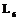- только одна, 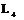- одна или 3, 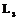- одна или 4, 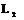- одна, две, три, четыре, шесть. Р – встречается одна, или в количестве .

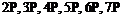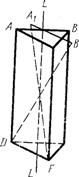
Рис. 5. Многогранник с инверсионной осью симметрии 6-го порядка

Порядок выполнения роботы:

1. Внимательно изучить полученные модели многогранников (заданные рисунки);

2. Определить наличие осей симметрии и их порядок;

3. Определить количество плоскостей симметрии;

4. Найти центр симметрии;

5. Выполнить рисунок многогранника и указать наличие на нем элементов симметрии;

6. Записать формулу симметрии;

Пример оформления: модель в виде куба, формула симмметрии 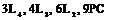(рисунки аналогичны рис. 3, рис. 4).

ПРАКТИЧЕСКАЯ РАБОТА №2