Состояния с отрицательной температурой

Состояния с отрицательной абсолютной температурой впервые были обнаружены в опытах с фтористым литием. При наложении электрического поля большинство ядерных спинов ориентируются по полю и лишь незначительная их часть из-за взаимодействия друг с другом – против поля. При быстром изменении направления магнитного поля не все спины успевают переориентироваться и поэтому в течении некоторого очень малого времени большинство спинов будет ориентировано против магнитного поля. Это означает, они будут распределены по энергетическим уровням таким образом, при котором на уровне с большей энергией число спинов больше, чем на более низком энергетическом уровне. Предположим, что энергия ядерного спина в магнитном поле равна при ориентации по направлению магнитного поля, и при ориентации против поля.

Очевидно, что будет выполняться неравенство .

Допустим, что число ядерных спинов – N. Причем из них ориентированы по полю, а – против. Тогда общая энергия ядерных спинов (пренебрегая энергией их взаимодействия) будет равна

.

Энергия взаимодействия ядерных спинов не вносит заметного вклада в энергетический баланс, но оно имеет существенное значение ибо может привести и удержать на некоторое время термодинамическую молекулярную систему в состоянии с вышеотмеченным распределением спинов. Благодаря ему рассматриваемое состояние может считаться статистически равновесным, а значит подчиняющимся закономерностям статистической термодинамики. Такой вывод вытекает из соотношения времен спин-спиновой и спин-решетчатой релаксации. Спин-спиновая релаксация имеет порядок времени 10^-5 с, спин-решетчатая релаксация – 10^-2 с.

В этом случае система спинов в промежутке времени от 10^-5 с до 10^-2 с после смены направления магнитного поля может рассматриваться как находящаяся в состоянии статистического равновесия. Строго говоря состояние спиновой системы с ориентацией против магнитного поля неравновесно и через 10^-2 с оно разрушается переходя в строго равновесное состояние.

Термодинамическая вероятность состояний при котором спинов ориентированы по полю, а - против равна

.

В соответствии с формулой Больцмана энтропия при этом будет составлять

,

или учитывая, что по теореме Стирлинга , формулу Больцмана можно свести к виду

.

Абсолютная температура системы равна частной производной , тогда

.

При выполняется условие , а в случае абсолютная температура окажется отрицательной, т.е. . Это позволяет сделать следующий вывод относительно состояний с отрицательной абсолютной температурой.

Такие состояния могут иметь место лишь в системах, у которых внутренняя энергия и не может принимать значений, больших некоторой конечной величины и_а и меньше некоторой конечной величины и₀.

.

Таким образом, рассмотренное выше состояние ядерных спинов некоторых парамагнитных материалов во внешнем магнитном поле, когда спины в основном ориентированы против магнитного поля, представляют собой неравновесное в целом (но метастабильное или квазиравновесное по отношению к достаточно малому промежутку времени) состояние с отрицательной температурой, а с ориентацией по полю – равновесное состояние с положительной температурой.

На основании вышеизложенного можно сделать вывод о том, что состояния при и тождественны ибо соответствуют одним и тем же значениям и .

В то же время состояния при и приводят к различным значениям внутренней энергии и , а значит существенно отличны друг от друга при одинаковых значениях и (т.к. при этом или ). Непрерывный переход между этими состояниями невозможен.

12 Флуктуации

Флуктуациями принято называть случайные отклонения физических величин (параметров состояния) от их равновесных значений.

Предположим, что в равновесном состоянии некоторый параметр состояния имеет значение , а при флуктуации причем по определению флуктуации .

Рассмотрим малую по величине флуктуацию, происходящую в изолированной системе и состоящую в том, что некоторая малая часть этой системы отклоняется от равновесного состояния.

В соответствии с формулой Больцмана вероятность какого-либо состояния изолированной системы равно

,

где - константа, - энтропия системы.

При флуктуации энтропия системы получает приращение , где - энтропия равновесной системы, - приращение энтропии системы при возникновении флуктуации. Вероятность рассматриваемой флуктуации составит

.

Изменение равновесного состояния системы неизбежно связано с затратой внешним источником работы необходимой для изменения равновесного состояния

,

Откуда после интегрирования получим

.

Интеграл в правой части берется по пути обратимого (квазистатического) перехода из состояния равновесия в новое состояния, достигаемое при флуктуации.

Для изолированной системы , . Температура системы при малых флуктуациях не может заметно отличаться от равновесной .

Тогда .

Подставим значение в выражение вероятности

. (12.1)

Мы получили основное соотношение для определения вероятности флуктуации.

В любой реальной термодинамической системе происходят флуктуации ее свойств.

Относительная величина флуктуаций обратно пропорциональна корню квадратному из числа молекул, составляющих систему.

12.1 Флуктуации плотности в газе

Тепловое движение молекул, из которых состоит газ, приводит к появлению флуктуации плотности, а как следствие и давления в газе. Решение задачи об этих флуктуациях можно выполнить на основе вычисления потенциальной энергии сжатия газа.

Рассмотрим некоторый контрольный объем газа, который в равновесном состоянии занимает объем и состоит из числа молекул. При температуре Т газ в равновесном состоянии имеет давление . Если этот газ с объемом несколько сжать до объема , то потребуется дополнительное давление, равное , а работа, необходимая для сжатия газа, найдется как

.

Сжатая таким образом порция газа имеет плотность, превышающую равновесную на , а ее давление было бы больше Р на .

Потенциальная энергия, соответствующая приросту плотности выделенного объема газа первоначально занимавшего объем с плотностью до неравновесной плотности +D , равна

.

Для тепловых флуктуаций средняя потенциальная энергия равна , если есть квадратичная функция переменной . Следовательно, квадратичная относительная флуктуация плотности выделенного контрольного объема газа, содержащего молекул равна

, (12.2)

то есть и для среднеквадратичной относительной флуктуации давления можно записать .

Чем меньше выделенный контрольный объем (чем меньше ), тем больше относительная флуктуация плотности и давления, порождаемая тепловым движением.

Если вести наблюдение за малым числом молекул, то их тепловое движение будет сравнительно сильно изменять их плотность. Если в выделенном контрольном объеме будет много молекул, то больше флуктуации в каждом малом объеме контрольного объема в значительной степени скомпенсируются, а среднеквадратичная относительная флуктуация контрольного объема в целом будет тем меньше, чем больше в нем молекул . Корень квадратный из среднеквадратичного значения относительной флуктуации плотности или давления выделенного объема газа обратно пропорционален корню квадратному из числа молекул в пробе.

Флуктуации плотности рассеивают звуковые и электромагнитные волны, когда те проходят через газ. Именно рассеяние света тепловыми флуктуациями в атмосфере порождает синий цвет неба. Эти флуктуации не зависят от температуры, хотя при более низких температурах молекул занимают меньший объем и сами флуктуации становятся более «мелкозернистыми».

Броуновское движение

Броуновское движение можно рассматривать как флуктуационное движение небольшой частицы, вызванное тепловыми флуктуациями давления. При этом среднее значение квадрата каждой компоненты скорости такого движения пропорционально температуре Т и обратно пропорционально массе.

На свободную частицу в жидкости действуют флуктуации давления, тяжести. При этом силы флуктуации давления вызывают флуктуационное движение, а силы вязкости препятствуют перемещению частицы. Любое значение х для частицы равновероятно. Пусть в начальном состоянии х=0 частица находилась в момент времени 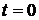. Среднее значение х при флуктуационном движении тоже равно 0. Однако ожидаемое значение х² со временем должно возрастать. Попробуем рассчитать ожидаемое значение х² как функцию времени и найдем плотность вероятности обнаружения частицы в х через время .

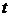Воспользуемся сравнительно грубой моделью одномерного броуновского движения. Пусть свободная частица движется линейно со скоростью . К концу каждого последовательного промежутка времени она может менять или не менять направление своего движения. Оба варианта при этом равновероятны (Р=1/2) и распределены случайно. После 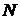интервалов, то есть через время , где – интервал, шанс, что частица сместится на величину от своего первоначального положения, равен шансу, что в течение п из 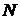интервалов она двигалась вправо, а в течение других интервалов – влево. За промежуток времени равный одному интервалу она покрывала расстояние .

Плотность вероятности находится как , где – среднее расстояние между соседними точками положения частицы.

Сама вероятность равна

.

Ожидаемое значение смещения , а дисперсия . Условная вероятность того, что частица в момент времени 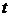находится в х, если х=0 при 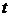=0 равна

, где .

Вероятность того, что частица в момент времени 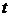находится между х и х+ , равна . То есть с течением времени 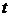“ширина” распределения возрастает, так как частица уходит от своего первоначального положения. Среднее значение квадрата х

. (12.3)

Таким образом с ростом времени 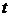величина возрастает линейно.

Уравнение Ланжевена

Для решения задачи реального броуновского движения частицы в жидкости необходимо найти величину постоянной 2 . Для этого требуется изучить уравнение ее движения. Проще изучить на примере одномерного движения.

Действующую на частицу х компоненту силы можно разбить на 2 части, одна из которых описывает усредненное влияние окружающей жидкости, а вторая обусловлена флуктуациями давления под воздействием теплового движения молекул жидкости. Сила трения имеет х компоненту равную (где х – скорость частицы в направлении координаты х). Механическое сопротивление движению в жидкости с вязкостью , для сферической частицы а равно как следует из закона Стокса. Флуктуирующую компоненту силы запишем как . Множитель М в этих силах, равен массе частицы. Это позволит нам в результирующем уравнении этот множитель устранить делением на М.

Запишем уравнение движения динамики для х – компоненты положения частицы

.

Это известное уравнение Ланжевена. – имеет размерность с^-1. Умножим уравнение Ланжевена на х/М

.

Воспользуемся тождествами

и ,

получим

.

Это выражение представляет собой уравнение, записанное для отдельной частицы. Если бы в жидкости было много одинаковых частиц, то каждая имела бы различные значения х и к концу заданного промежутка времени 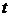из-за влияния случайной силы .

Усредним действие флуктуации усреднением слагаемых уравнения по всем подобным частицам. Член при этом выпадает, так как и и равны нулю, а флуктуации х и А независимы. Среднее значение включает в себя усредненные эффекты флуктуирующие силы . Для частицы в тепловом равновесии при температуре Т, среднеквадратичное значение компоненты ее скорости равно .

Усреднение приведенного выше дифференциального уравнения дает

.

Решение последнего уравнения может быть записано в виде

.

Слагаемое, содержащее временную экспоненту, довольно быстро исчезает и остается стационарное решение

.

Тогда .

Для сферической частицы радиуса а в жидкости с вязкостью и закона Стокса получим

. (12.4)

Это уравнение позволило Перрену с сотрудниками впервые измерить число Авогадро.

Измерив вязкость жидкости , в которую были потом погружены частицы известного радиуса а, зная температуру жидкости Т и проследив за изменениями координат частицы в начале и конце каждого из последовательных промежутков времени 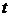можно вычислить среднее значение для ряда величин , что эквивалентно .

Измерения были проведены неоднократно для различных промежутков времени 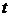и на их основании подтверждено равенство , откуда найдена величина .

Тогда число Авогадро может быть вычислено как

. (12.5)

Точность вычислений составляет 0,5% со значениями, найденными позднее более прямыми измерениями. Чтобы было возможно больше, размеры частиц должны быть более меньшего размера. У Перрона частицы имели радиус а=2×10^{-5 см, а 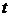изменялось от нескольких секунд до минуты с лишним.}

Уравнение Фоккера - Планка

Достаточно очевидно, что броуновское движение выявляет просто некоторые характерные особенности процесса молекулярной диффузии. Коэффициент диффузии для частицы в жидкости равен . В молекулярном случае , в то время как для крупной сферической частицы . Средняя концентрация диффундирующих частиц должна удовлетворять уравнению диффузии, имеющему вид аналогичный уравнению теплопроводимости

,

где - поток меченных i-х частиц в точке , - радиус-вектор.

Плотность вероятности присутствия частицы в точке пространства в момент времени t, если она начинает перемещаться из (при ), описывается трехмерным уравнением

; ,

представляющим собой по сути решение дифференциального уравнения диффузии. Значение берется для изучаемой частицы.

Когда на диффундирующую частицу действует внешняя сила , то уравнение диффузии имеет более общий вид

. (12.6)

В том случае, когда есть плотность диффундирующей субстанции (молекул или теплоты), то записанное выражение называют уравнением диффузии. Если - функция распределения для частицы, совершающей броуновское движение, а уравнение рассматривается как первое приближение к обобщенному уравнению Ланжевена, таким образом, последнее выражение известно как уравнение Фоккера - Планка. Решение уравнения (12.6) было записано нами выше. Из него можно получить все необходимые характеристики броуновского движения по отношению к возможному положению частицы в момент времени t.

Уравнение Фоккера - Планка может быть выведено и для распределения импульсов

.

Для частицы, которая начала двигаться с импульсом при , решение этого уравнения дает плотность вероятности частицы в импульсном пространстве

.

Откуда следует, что ожидаемый импульс частицы в момент времени t равен . Т.е. мы видим, что это есть импульс частицы начавшей двигаться с импульсом и испытывающей тормозящей силу трения . С течением времени действие флуктуаций “размазывает” распределение частиц по импульсам, и дисперсия импульса (т.е. его среднеквадратичное отклонение от ) равна , начинается с 0 при , когда мы знаем, что импульс частицы равен и он приближается со временем к величине , которая типична для распределения по Максвеллу. Последнее уравнение показывает, как первоначально неравновесное распределение для частицы (или молекулы) может превратиться с течением времени в распределение по Максвеллу, характерное для равновесного состояния. Постоянная , равная для частицы сферической формы или для молекулы в газе, равна обратной величине времени релаксации для распределения.

Наиболее общей формой функции распределения была бы функция , дающей распределение и по координатам, и по импульсам в момент времени

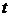
. (12.7)

13 Термодинамические потенциалы