Свойства вещества в критическом состоянии
Критическая точка на линии насыщения характерна тем, что в ней исчезают различия между жидкой и газовой фазами. Запишем очевидное условие равенства удельных объемов.

Кроме того, изотерма, соответствующая критической точке имеет горизонтальную касательную. В этом случае с точки зрения дифференциальной математики должны выполняться условия
 . (8.17)
. (8.17)
Выражения (8.18) подчеркивают, что на Р,V-диаграмме в критической точке изотерма имеет не только горизонтальную касательную, но и перегиб. В этом случае величина подкасательной равна  , т. е.
, т. е.
 .
.
Эксперименты показывают, что на линии насыщения кривые  и
и  имеют в критической точке вертикальные касательные, а производные
имеют в критической точке вертикальные касательные, а производные  и
и  отрицательны, тогда справедливы соотношения
отрицательны, тогда справедливы соотношения
 . (8.18)
. (8.18)
 Рисунок 8.11 V, T–диаграмма состояния вещества Рисунок 8.11 V, T–диаграмма состояния вещества |
Анализ состояния и поведения критической изобары в  – диаграмме показывает, что в критической точке производные
– диаграмме показывает, что в критической точке производные 
 , (8.19)
, (8.19)
 ,
,
а полная производная от удельного объема по температуре  приобретает бесконечно большое значение
приобретает бесконечно большое значение
 ;
;  . (8.20)
. (8.20)
Под линиями кипения и концентрации в T, S – диаграмме расположена область двухфазных состояний влажного пара, представляющего собой жидкость, находящуюся в состоянии динамического равновесия с сухим насыщенным паром. Линии конденсации и кипения сходятся в критической точке 
В двухфазной области изобары совпадают с изотермами, т. е. расположены горизонтально. В области жидкости изобары расположены очень близко друг к другу и поэтому при изоэнтропном сжатии температура повышается незначительно. Тепло подводимое и отводимое в обратимых процессах изображается в T, S – диаграмме площадью под процессом. Подкасательные к изобарам и изохорам характеризуют удельные теплоемкости  и
и  .
.
На i, 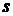 – диаграмме также в первую очередь находятся границы области насыщения по соответствующим табличным значениям. Изобары в гомогенной области как и изохоры представляют собой слабо изогнутые кривые
– диаграмме также в первую очередь находятся границы области насыщения по соответствующим табличным значениям. Изобары в гомогенной области как и изохоры представляют собой слабо изогнутые кривые
 , для
, для  , чем > T, тем круче изобары.
, чем > T, тем круче изобары.
 Рисунок 8.12 Рисунок 8.12 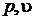 -диаграмма реального вещества -диаграмма реального вещества |
 Рисунок 8.13 Т, S – диаграмма реального вещества Рисунок 8.13 Т, S – диаграмма реального вещества |
Влажный пар
9.1 Процесс парообразования
Под влажным паром будем понимать равновесную смесь кипящей жидкости и сухого насыщенного пара. При таком состояния для обеих фаз в двухфазной области выполняется условие  и
и 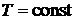 . Кипящей жидкости соответствует положение на линии кипения. Точка, определяющая состояние системы находится на левой граничной кривой, т. е. слева от критического состояния. Сухой насыщенный пар – газ, состояние которого находится на правой от критического состояния части граничной кривой. (рисунок 9.1, 9.2)
. Кипящей жидкости соответствует положение на линии кипения. Точка, определяющая состояние системы находится на левой граничной кривой, т. е. слева от критического состояния. Сухой насыщенный пар – газ, состояние которого находится на правой от критического состояния части граничной кривой. (рисунок 9.1, 9.2)
 Рисунок 9.1 р, Рисунок 9.1 р, 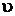 -диаграмма процесса образования пара -диаграмма процесса образования пара |
 Рисунок 9.2 Т, S-диаграмма процесса образования пара Рисунок 9.2 Т, S-диаграмма процесса образования пара |
На диаграммах изображен процесс парообразования для воды при давлении насыщающих паров  . Пусть при
. Пусть при  – температуре окружающей среды вода в жидком состоянии имеет удельный объем
– температуре окружающей среды вода в жидком состоянии имеет удельный объем 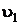 (состояние 1). По мере нагрева с ростом температуры
(состояние 1). По мере нагрева с ростом температуры 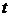 незначительно возрастает удельный объем. При достижения температуры кипения 99,6 °С образуются первые паровые пузырьки, число которых по мере дальнейшего нагрева возрастает. Вода кипит, при этом давление и температура остаются неизменными, а удельный объем пара по мере нагрева возрастает. Пар в этом состоянии влажный и состоит из смеси сухого насыщенного пара, находящегося в динамическом равновесии со своей кипящей жидкостью. В точке
незначительно возрастает удельный объем. При достижения температуры кипения 99,6 °С образуются первые паровые пузырьки, число которых по мере дальнейшего нагрева возрастает. Вода кипит, при этом давление и температура остаются неизменными, а удельный объем пара по мере нагрева возрастает. Пар в этом состоянии влажный и состоит из смеси сухого насыщенного пара, находящегося в динамическом равновесии со своей кипящей жидкостью. В точке  испарилась последняя капля жидкости, и вода представляет собой сухой насыщенный пар.
испарилась последняя капля жидкости, и вода представляет собой сухой насыщенный пар.
При дальнейшем нагреве в процессе  температура пара возрастает, и мы будем иметь воду в состоянии перегретого пара. Описанный процесс парообразования будет иметь место лишь при давлениях меньше критического. При давлениях
температура пара возрастает, и мы будем иметь воду в состоянии перегретого пара. Описанный процесс парообразования будет иметь место лишь при давлениях меньше критического. При давлениях  заметной разности между жидким и газообразным состоянием нет и двухфазной области вещества не существует. Переход из жидкого в парообразное осуществляется в процессе непрерывного накопления жидкостью свойств пара.
заметной разности между жидким и газообразным состоянием нет и двухфазной области вещества не существует. Переход из жидкого в парообразное осуществляется в процессе непрерывного накопления жидкостью свойств пара.
Каждому давлению соответствует определенная температура кипения. Каждой температуре соответствует свое давление насыщающих паров. Зависимость давления насыщающих паров от температуры кипения представляет собой уравнения парообразования
 (9.1)
(9.1)
