Внутренняя энергия Ван-дер-Ваальсовского газа
Найдем внутреннюю энергию Ван-дер-Ваальсовского газа. Она состоит из кинетической 
и потенциальной 
составляющих внутренней энергии
. (8.4)
Допустим, что моль газа помещен в упругую адиабатическую оболочку. Давление на оболочку со стороны газа изнутри уравновешено внешним давлением.
Пусть газ незначительно расширяется на величину 
. Совершенная при этом элементарная работа расширения должна быть по величине равна убыли внутренней энергии системы 
, т. к. притока тепла нет 
, т. е.
.
Если устранить каким-либо способом взаимодействие между молекулами, то давление на оболочку станет равным 
, а 
. Тогда
и взяв разность двух последних выражений, получим, что 
равно
.
Проинтегрировав его, получим
.
Интегрирование осуществлялось по объему, поэтому константа может быть лишь функцией температуры или просто постоянной величиной.
Таким образом, можно записать для потенциальной составляющей внутренней энергии
.
Если 
, то последнее выражение должно переходить в зависимость для внутренней энергии идеального газа. Тогда очевидно, что 
и
. (8.5)
Внутренняя энергия n молей будет в n раз больше.
Выражение критических параметров
через коэффициенты a и b
Запишем уравнение Ван-дер-Ваальса
.
Раскроем скобки
.
 Рисунок 8.5 Изотермы Ван-дер-Ваальса |
Получилось кубическое уравнение относительно объема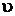 
, коэффициенты которого зависят от параметров состояния р и Т. В зависимости от их численной величины уравнение имеет три решения:
1) все три корня вещественные и одинаковые;
2) все три корня вещественные разные;
3) один корень вещественный, а два других – комплексные.
Комплексные решения не имеют физического смысла.
Температура для каждого газа, начиная с которой при любом давлении 
уравнение будет иметь лишь одно решение, называется критической.
Само состояние тоже принято называть критическим 
. Для критической изотермы точка К является точкой перегиба 
, 
. Решим уравнение Ван-дер-Ваальса относительно давления
.
Продифференцируем его по 
; 
.
Положив 
, 
, 
, найдем связь между критическими параметрами и константами уравнения Ван-дер-Ваальса.
Составим систему уравнений
.
Решение системы уравнений дает
; 
; 
. (8.6)
Подставляя значения для 
, получим
.
Экспериментальные изотермы
Как следует из теоретического анализа изотерм Ван-дер-Ваальса при давлении 
для каждого газа существует область таких объемов, где вещество ведет себя неестественным образом: рост объема при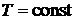 
сопровождается постоянством давления. Однородного вещества с такими свойствами быть не может. Следовательно, в этой области вещество становится неоднородным, т. е. оно расслаивается на две фазы: жидкую и газообразную – паровую.
| Рисунок 8.6 Экспериментальные изотермы реального газа – кривые Эндрюса | Рисунок 8.7 Зависимость плотности жидкости и насыщенного пара от температуры |
Экспериментальные графики изотерм реальных жидкостей и газов отличаются от Ван-дер-Ваальсовских горизонтальным участком сменяющим синусоидальную область. Можно выделить три области: жидкую – Ж, паровую – П и двухфазную, в которой жидкость находится в состоянии равновесия со своим насыщенным паром. Давление, при котором наблюдается это равновесие, принято называть давлением насыщающих паров. Как видно, с ростом давления насыщающих паров протяженность горизонтального участка уменьшается постепенно стягиваясь в точку при критической температуре 
. Насыщенный пар может существовать лишь при температуре ниже критической.
Фазовые превращения
Разные фазы одного и того же вещества могут находиться в равновесии, соприкасаясь друг с другом. Такое равновесие имеет место лишь в ограниченном интервале температуры. Каждому значению температуры соответствует свое значение давления р, при котором это равновесие возможно.
На экспериментальной изотерме совокупность равновесных состояний изображается отрезком горизонтальной прямой. Состояния, отвечающие различным точкам участка, отличаются распределением вещества между фазами. Концам горизонтального отрезка соответствуют однофазные состояния. Вся совокупность состояний, изображаемая в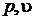 
– диаграмме отрезком прямой, на диаграмме 
будет представлена одной точкой, определяющей значение р и Т, при которых осуществляется переход.
Переход вещества из одной фазы в другую обычно происходит с поглощением либо выделение энергии в форме тепла, которое называют теплотой фазового перехода. Например, при таянии льда теплота поглощается – это теплота плавления, при замерзании воды выделяется такое же количество теплоты. Изменения агрегатного состояния, сопровождаемые тепловыделением либо теплопоглощением, принято называть фазовыми переходами первого рода.
Существуют превращения одной кристаллической модификации в другую, не связанные с тепловыми эффектами поглощения или выделения, которые принято называть фазовыми переходами второго рода.
При этомплотность вещества остается неизменной. Скачкообразно изменяется теплоемкость и некоторые другие физические характеристики. При температуре Кюри железо из ферромагнитного состояния переходит в парамагнитное. К числу фазовых переходов второго рода относится переход в сверхпроводящие состояния жидкого гелия, совершаемый при отсутствии магнитного поля.
 Рисунок 8.8 Диаграмма состояния вещества |
Три фазы одного и того же вещества могут находится в равновесии лишь при единственных значениях давления и температуры. Точка на диаграмме, соответствующая этому состоянию называется тройной точкой. В тройной точке сходятся три кривые равновесия фаз: плавления, испарения и сублимации.
Сублимацией или возгонкой называется непосредственный переход из кристаллического состояния в газообразное. Диаграмма р, Т называется диаграммой состояния вещества. Их строят обычно на основании опытных данных. Процесс 1-2 предполагает последовательный переход из твердого состояния в газообразное через промежуточное жидкое. Процесс 3-4 переход из твердого в газообразную фазу возгонкой (т. е. минуя жидкую фазу).