Анализ политропного процесса

Политропными называется класс термодинамических процессов, при протекании которых неизменно одно и тоже количество подводимого тепла идет на изменение внутренней энергии.

Термодинамический процесс, при протекании которого теплоемкость остается постоянной, относится к политропным:

.

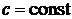Политропные процессы – это процессы, которые протекают при постоянном для данного процесса показателе политропы .

Найдем уравнение политропного процесса. Для этого запишем уравнение первого начала термодинамики через внутреннюю энергию и энтальпию:

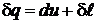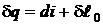, . (5.1)

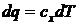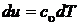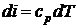Вспоминая, что , , а , перепишем уравнения в виде, считая термодинамическую систему, состоящую из идеального газа 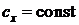и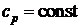

, .

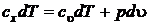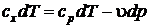Выразим из (5.1) теплоемкость процесса :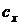

, .

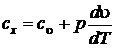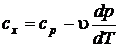После несложных преобразований получим

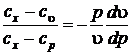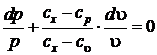; . (5.2)

Введём обозначение

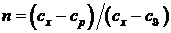. (5.3)

Тогда дифференциальное уравнение политропного процесса (5.2) с учетом обозначений (5.3) запишется в виде

.

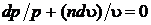Проинтегрируем полученное дифференциальное уравнение

.

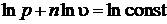Откуда после потенциирования получим уравнение политропного процесса:

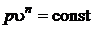, (5.4)

где – показатель политропы (5.3)

Выражение (5.3) можно решить относительно теплоемкости процесса « »: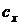

; .

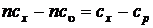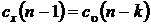Тогда выражение для расчета теплоемкости любого произвольного политропного процесса может быть найден из зависимости (5.5)

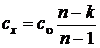. (5.5)

Изобразим политропный процесс в р, u – и T, S – диаграммах

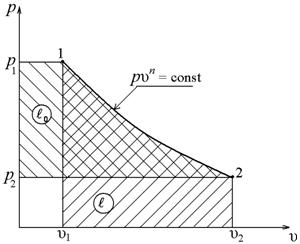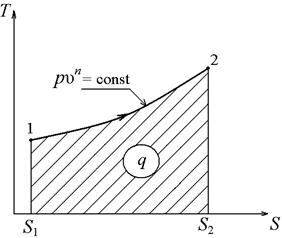Рисунок 5.1 р, u – диаграмма политропы

Рисунок 5.2 T, S – диаграмма политропы

Изменение внутренней энергии за процесс

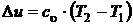. (5.6)

Изменение энтальпии за процесс

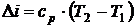. (5.7)

Количество тепла подведенное (отведенное) в процессе

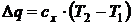. (5.8)

Запишем выражение для расчета элементарной работы за процесс .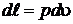

Если состояние системы в процессе изменяется от удельного объема 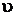, до 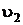то результирующую работу найдем интегрированием.

.

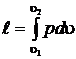Из уравнения процесса 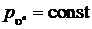выразим давление , подставим его в выражение интеграла и проинтегрируем:

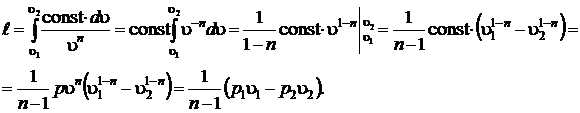
Таким образом удельная работа расширения в политропных процессах определяется выражением (5.9)

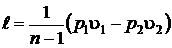. (5.9)

Удельная величина располагаемой работы равна .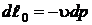

Конечная за процесс величина располагаемой работы может быть найдена интегрированием бесконечно малого изменения 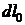от начального давления 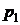системы до его конечного значения в процессе .

.

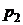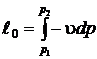Запишем удельный объем 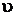через параметр 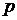воспользовавшись опять уравнением процесса

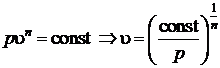
Подставим полученное выражение в интеграл для расчета располагаемой работы и проинтегрируем

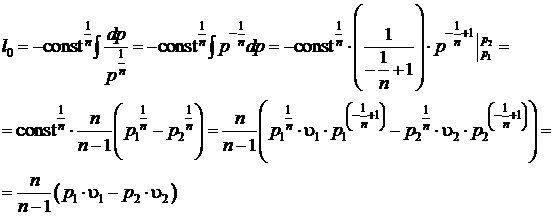
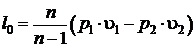(5.10)

Таким образом сопоставляя выражения для расчета работы расширения (5.9) в политропном процессе с располагаемой работой (5.10) отметим, что последнее в раз больше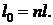

Найдем изменение энтропии в процессе. Для этого воспользуемся уравнением первого начала термодинамики в дифференциальной форме

.

Перепишем его в виде объединенного уравнения 1^го и 2^го начал через внутреннюю энергию 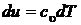и энтальпию 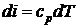, , 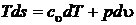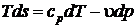. Выразим из последних выражений дифференциал энтропии

, .

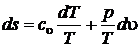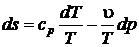Воспользуемся уравнением состояния идеального газа 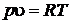и выразим давление 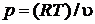и удельный объем 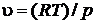. После подстановки полученных выражений в зависимости для расчета энтропии получим

, ,

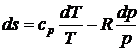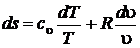или после интегрирования

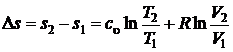, (5.11)

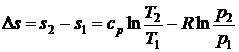. (5.12)

Часть тепла, пошедшая на изменение внутренней энергии

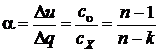. (5.13)