Энтропия и второй закон термодинамики

Энтропия – параметр состояния, позволяющий дать количественную формулировку Второго закона термодинамики. Термодинамическая система может быть охарактеризована экстенсивным параметром состояния – энтропией S, дифференциал которой для обратимых процессов определяется соотношением

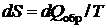. (4.2)

Воспользуемся Первым началом термодинамики, переписав выражение (4.2) в виде

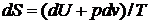, (4.3)

где Т – термодинамическая температура.

Энтропия объединенной системы, состоящей из подсистем А,В,С... равна, в соответствии со свойством аддитивности равна, сумме энтропий входящих в нее подсистем

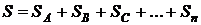, (4.4)

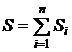. (4.5)

Энтропия адиабатной термодинамической системы не может уменьшаться

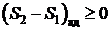. (4.6)

Размерность энтропии S [Дж/К], удельной энтропии s [Дж/кгК].

Для большинства систем в термодинамике энтропия зависит лишь от двух параметров

Рисунок 4.1 Адиабатный процесс

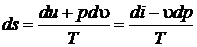. (4.7)

Интегральное изменение энтропии справедливо для любого квазистатического изменения состояния 1-2

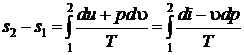. (4.8)

Значение разности энтропий 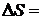S₂ – S₁ не зависит при этом от пути интегрирования, а однозначно определяется состояниями 1 и 2. Это подчеркивается тем фактом, что энтропия является параметром состояния.

Формулировка Второго закона термодинамики особенно наглядна для адиабатной системы, энтропия которой либо возрастает, либо остается неизменной. Применяя Второй закон термодинамики к неадиабатной системе, следует помнить, что она в сочетании с другими системами, с которыми обменивается теплом, составляет совокупную адиабатную систему. Каждая неадиабатная подсистема в ходе термодинамического процесса испытывает свое определенное изменение энтропии

,

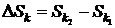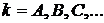
причем это изменение 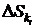может быть положительным, отрицательным или равным нулю. Однако сумма всех приращений для каждой подсистемы в результате не может быть отрицательной. В этом и состоит суть Второго начала

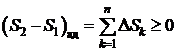(4.9)

Применение Первого и Второго законов термодинамики

К изолированным системам

Процессы, протекающие в изолированных системах, в том числе и самопроизвольные, связанные с выравниванием параметров, должны удовлетворять условиям

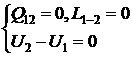(4.10)

Но изолированная система адиабатна и поэтому в соответствии со Вторым законом термодинамики при отсутствии теплообмена энтропия остается неизменной либо возрастает

.

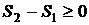Все процессы в изолированных системах протекают таким образом, что внутренняя энергия ее остается неизменной, а энтропия возрастает вследствие необратимости протекающих процессов до некоторого максимума.

Состояние с максимально возможной энтропией соответствует равновесию изолированной системы.

Клаузиус выразил содержание уравнени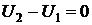й и 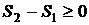формулировкой: “Энергия мира постоянна, энтропия мира стремится к максимуму”. Эта формулировка привела к философским спекуляциям и к необоснованно пресловутому положению о неизбежности тепловой смерти. Однако выводы Первого и Второго начал были получены для систем конечных размеров и изолированных, поэтому отмеченные положения вряд ли разумно распространять на бесконечные системы, изолированность которых никак не доказана.