Основы молекулярно-кинетической и квантовой

Теории теплоемкости

Основной предпосылкой кинетической теории газов является установленный Максвеллом и Больцманом закон о равномерном распределении энергии по степеням свободы поступательного и вращательного движений молекул газа. Из молекулярно-кинетической теории известно, что у одноатомного газа молекула имеет i = 3 степени свободы поступательного движения, у двухатомной молекулы газа к трем степеням свободы поступательного движения добавляются еще две степени свободы вращательного движения и их общее число равно 5. У трехатомных молекул и многоатомных вращательных степеней свободы 6. Для идеального газа (совершенного газа – газа подчиняющегося уравнению Клапейрона-Менделеева) внутренняя энергия однозначно определяется температурой и рассчитывается по зависимости, полученной из анализа основного уравнения молекулярно-кинетической теории. Запишем выражение для расчета внутренней энергии одного моля идеального газа:

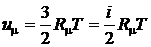. (2.53)

где 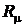= 8,3142 [Дж/моль×К] – универсальная газовая постоянная; i – число степеней свободы. Тогда после постановки численного значения универсальной газовой постоянной для идеального газа получим

.

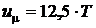Продифференцируем внутреннюю энергию по температуре при постоянном объеме, считая, что

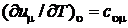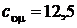; Дж/моль×К.

Очевидно, что на каждую степень свободы молекулы приходится одна треть от рассчитанной выше

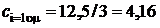Дж/моль×К.

Теперь можно рассчитать теплоемкости двухатомных, трех и многоатомных газов, считая их совершенными, т. е. подчиняющимися уравнению Клапейрона-Менделеева.

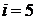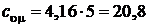Для двухатомного газа , а Дж/(моль×К);

Для трехатомного газ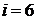а , а 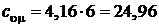Дж/(моль×К);

Однако при сравнительно высоких температурах экспериментально полученные значения теплоемкостей заметно отличаются от рассчитанных на основе положений МКТ. Это связано с тем, что в приведенной модели не учитывалась энергия, приходящаяся на степени свободы внутримолекулярного и внутриатомного движений, а также энергия, связанная с взаимодействием молекул, зависящая от изменения объема при изменении температуры. Попытка учета этих составляющих связана с тем, что атомы в молекуле не всегда жестко связаны друг с другом и могут совершать колебания друг относительно друга. Тогда для определения конфигурации молекулы требуется ввести еще одну координату. Это координата – расстояние между молекулами. Таким образом двухатомная молекула будет обладать 6-ю степенями свободы: 3 – поступательные, 2 – вращательные и 1 – колебательная степень свободы.

Если молекула состоит из n атомов, нежестко связанных между собой, то она имеет 3n степени свободы, из которых 3 – поступательные, 3 – вращательные, а остальные колебательные. Таким образом, нелинейная молекула из n атомов имеет 3n – 6 колебательных степеней свободы, а у линейных 3n – 5.

Колебательные степени свободы возбуждаются при высоких температурах. При достаточно малых амплитудах колебания атомов можно считать гармоническими осцилляторами.

Для гармонического осциллятора средние значения потенциальной и кинетической энергии равны между собой. Если в молекуле возбуждаются гармонические колебания, то по закону равнораспределения на каждую колебательную степень свободы приходится 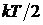в виде кинетической и 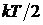в виде потенциальной энергии. Тогда формула для подсчета числа степеней свободы будет иметь вид

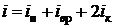(2.45)

Эйнштейн, воспользовавшись квантовой теорией Планка, получил следующее выражение для мольной теплоемкости, достаточно точное для температур, применяемых в теплотехнике.

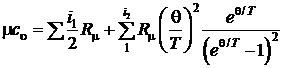, (2.46)

где 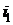– число степеней свободы поступательного движения и вращательного;

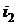– число степеней свободы внутримолекулярных колебаний;

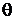– характеристическая температура колебательного движения,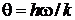

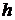( – постоянная Планка);

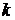– постоянная Больцмана;

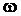– частота колебаний в секунду;

е – основание натуральных логарифмов;

Т – температура.

В приведенной выше формуле первый член учитывает количество теплоты, расходуемое на увеличение поступательного и вращательного движения молекул и определяется числом степеней свободы этих движений. Второй член учитывается количество теплоты, расходуемое на увеличение внутримолекулярных колебаний.

ГАЗОВЫЕ СМЕСИ

Практически во всех сферах деятельности мы сталкиваемся не с веществами в чистом виде, а с их химическими соединениями, либо с механически перемешенными веществами или растворами. К примеру, рабочие тела почти всех тепловых машин представляют собой некоторую газовую смесь. Не составляет исключение и воздух, которым мы дышим и используем в большинстве случаев как окислитель в камерах сгорания двигателей, топках различных топливосжигающих устройств. Как известно, воздух состоит из 78,08 % азота N₂, 20,95 % кислорода О₂, и где-то около 1 % составляют примеси других газов. С экологической точки зрения хотелось бы, чтобы процент примесей не возрастал в результате не всегда разумного вмешательства человечества в естественные массообменные процессы природы.

При термодинамических расчетах рабочих процессов тепловых машин мы сталкиваемся с необходимостью определения термодинамических параметров рабочих тел, в подавляющем большинстве случаев представляющих собой газовую смесь продуктов сгорания углеводородных топлив, что требует умения и навыков расчета газовых смесей. Следовательно, должны быть разработаны методы их расчета и способы задания газовых смесей.

3.1 Способы задания газовой смеси

Под смесью идеальных газов понимается механическая смесь химически обособленных исходных газов, подчиняющихся уравнению состояния идеального газа. Тогда будем считать, что и смесь представляет из себя некоторый самостоятельный идеальный газ, термодинамические свойства которого определяются количественным соотношением входящих в него исходных компонентов, т. е. свойства газовой смеси однозначно определяются ее составом.

Состав газовой смеси определяется количественным соотношением входящих в него компонентов и может быть задан массовыми, объемными или мольными долями.

Пусть М_см – масса газовой смеси, а т_i – масса i-го компонента, входящего в смесь. Согласно закону сохранения массы будем иметь очевидное равенство:

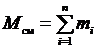, (3.1)

где n – число компонентов смеси.

Под массовой долей i-го компонента будем понимать отношение:

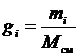или в процентах 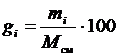%. (3.2)

На основании закона сохранения вещества, запишем уравнение баланса массы:

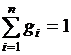. (3.3)

Если массовые доли заданы в процентах, то

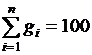%. (3.4)

Объемные доли представляют собой отношение парциальных объемов компонентов к объему газовой смеси:

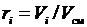, (3.5)

где V_i – парциальный объем i-го компонента; V_см – объем газовой смеси.

Под парциальным объемом будем понимать тот объем, которым бы обладал i-й компонент, находясь при температуре 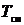и давлении 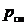газовой смеси.

Нетрудно показать, что парциальные объемы газов прямо пропорциональны их парциальным давлениям. Парциальным называется давление, которое создавал бы i-й газ смеси, если бы он один занимал весь объем смеси, находясь в нем при температуре смеси. Запишем уравнение Бойля-Мариотта для компонента смеси:

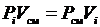, т. е. (3.6)

,

или

, ,

где P_i – парциальное давление i-го компонента; V_i – парциальный объем

i-го компонента.

Сложим почленно левые и правые части закона Бойля-Мариотта для компонентов:

или .

Согласно закону Дальтона

, (3.7)

тогда . (3.8)

Объем газовой смеси равен сумме парциальных объемов компонентов, входящих в смесь. Это утверждение равносильно равенству

или %. (3.9)

Состав газовой смеси может быть задан и числом молей, входящих в нее компонентов

(3.10)

где – число молей смеси; – число молей i-го компонента.

Тогда под мольной долей будем понимать отношение

(3.11)

и, согласно закону сохранения количества вещества, будем иметь равенство

или %. (3.12)

Воспользуемся следствием из закона Авогадро: одинаковые количества различных идеальных газов, находящихся при одинаковых давлениях и температуре, занимают одинаковые объемы.

Запишем , но ,

тогда , (3.13)

т. е. объемные и мольные доли компонентов смеси равны между собой.