Уравнение первого закона термодинамики

а) для закрытой системы

В соответствии с определением первого начала энергия, подведенная к системе, расходуется на изменение внутренней энергии и на совершение работы.

Если система не поточная, закрытая, то энергию можно подвести лишь в форме тепла и работы. При этом работа связана лишь с изменением объема. Тогда математическая запись первого начала примет вид:

. (2.21)

– подведенное элементарное тепло,

– изменение внутренней энергии,

– элементарная работа расширения.

>0 – тепло подводится с системе;

<0 – тепло отводится от системы;

>0 – внутренняя энергия и температура растут;

<0 – внутренняя энергия и температура падают;

>0 – работа совершается системой;

<0 – работа совершается над системой.

б) для поточной системы

Рассмотрим течение жидкости или газа в канале произвольной формы (рисунок 2.5).

Рисунок 2.5 К выводу уравнения Первого начала термодинамики для поточной системы

Поскольку потери массы через стенки канала (трубки тока) невозможны, выполняется уравнение сохранения расхода .

На На выходе эта энергия составит , G – массовый расход вещества через канал.

Изменение кинетической энергии по длине выделенного участка составит

.

Запишем уравнение первого начала термодинамики

.

Индексы относятся к выделенным сечениям.

Определим работу потока.

Для того, чтобы через сечение 1 ввести в канал в единицу времени массу G, нужно совершить некоторую работу на то, чтобы вытолкнуть предшествующую порцию. При этом работа совершается окружающей средой над системой и, следовательно, в соответствии с принятым правилом знаков она отрицательна

,

где р₁ – давление в сечении 1; S₁ – площадь этого сечения; DX₁ – перемещение G массы газа.

Но , очевидно, что . Работа совершается против системы, тогда .

Рассуждая аналогично, получим: – работа совершается потоком.

Таким образом, на протекании G количества газа в единицу времени между сечением 1-2 совершается работа, равная алгебраической сумме вышеприведенных работ, которую в термодинамике принято называть работой проталкивания

, [Дж]

Работа проталкивания pu – это такая работа, которую нужно совершить, чтобы систему объемом u поместить в среду давлением р.

Элементарная работа проталкивания

.

Первое слагаемое связано с работой затраченной на изменение объема.

Вторая составляющая работы потока пошла на приращение кинетической энергии

.

Третья составляющая работы затрачивается на приращение потенциальной энергии струи, связанное с изменением положения центра масс поперечного сечения струйки потока относительно нулевого уровня потенциальной энергии

.

Четвертая составляющая – техническая работа (турбина, компрессор и т. д.).

Пятая составляющая – работа по преодолению диссипативных сил – трение, турбулизация потока и т. д. ( , ).

Тогда работа, которая может совершаться движущимся потоком в общем случае, может быть записана в виде

.(2.22)

Воспользуемся уравнением первого закона термодинамики для потока вещества

(2.23)

Или в дифференциальной форме для единицы расхода через канал после деления на расход G

, (2.24)

или через энтальпию

. (2.25)

В конечных величинах для 1 кг вещества в потоке уравнение первого начала имеет вид:

, (2.26)

, (2.27)

где i – удельная энтальпия – тепловая функция , Дж/кг.

Величина q – полное тепло, подведенное к потоку, она равна сумме тепла, подведенного через границы системы за счет теплообмена и внутреннего – , обусловленного действием диссипативных сил (трение, турбулентность и т. д.).

.

Тогда .

В связи с очевидным равенством

,

последнее выражение может быть переписано в виде

. (2.28)

Итак, мы получим уравнение первого начала термодинамики для любой системы и для потока вещества через систему

.

На основании идентичности уравнений приравняем их правые части с учетом того, что

После сокращений, получим

Тогда для любого потока вещества справедливо равенство

(2.29)

Для случая, когда ; ; получим

. (2.30)

Изменение кинетической энергии системы численно равно величине технической работы, совершаемой системой или над ней.

Энтальпия

Под энтальпией понимается тепловая функция представляющая собой полную энергию системы, состоящую из внутренней энергии u и работы затраченной на проталкивание .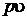

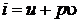. (2.31)

Энтальпия включает в себя все слагаемые, являющиеся параметрами состояния, поэтому ее дифференциал будет полным, а циркуляция от него по замкнутому контуру равна нулю.

.

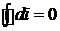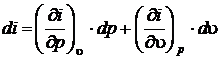
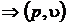
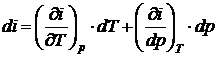
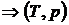(2.32)

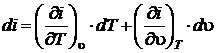
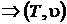
Энтальпия подчиняется закону аддитивности по сути своей являясь экстенсивным параметром 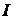,[Дж]. Чаще всего в расчетах используют удельную энтальпию i, [Дж/кг]

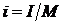, [Дж/кг], (2.33)

где М – масса вещества в системе.

Уравнение первого начала термодинамики может быть записано через энтальпию и располагаемую работу. Запишем выражение для полного дифференциала энтальпии

.

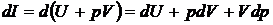Первое начало термодинамики имеет вид

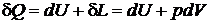
Из выражения для дифференциала энтальпии выразим сумму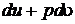

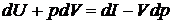
Тогда после подстановки получим

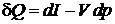(2.34)

или для 1 кг вещества в системе

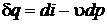(2.35)

Подведенная теплота расходуется на изменение энтальпии системы и на совершение располагаемой (технической) работы.

Теплоемкость газов

Одним из проявлений взаимодействия термодинамической системы с окружающей средой является изменение температуры термодинамической системы (исключение – изотермический процесс). Обмен теплом между системой и средой оценивается экстенсивным параметром состояния – теплоемкостью, истоки которого идут еще от теплорода.

Под теплоемкостью понимают количество теплоты, которое необходимо подвести (отвести) к термодинамической системе по какому-либо процессу с тем, чтобы изменить ее температуру на 1 Кельвин.

Теплоемкость конкретного вещества зависит от его физических свойств, агрегатного состояния в котором оно находится, от температуры и в некоторой степени от давления.

В газообразном состоянии основное влияние на теплоемкость веществ оказывает температура. В этом случае разумно ввести в рассмотрение среднюю и истинную теплоемкости, понимая под последней теплоемкость при данной конкретной температуре.

Под средней теплоемкостью в интервале температур 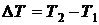понимается отношение:

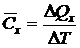, [Дж/К] (2.36)

где 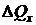– количество теплоты, полученное телом в процессе изменения ее температуры на величину 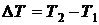. Индекс “x” указывает на характер процесса подвода теплоты.

Под истиной теплоемкостью будем понимать предел отношения

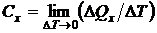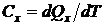; , [Дж/К] (2.37)

Теплоемкость системы является экстенсивным параметром. Интенсивные свойства отражают удельные теплоемкости, т. е. теплоемкости отнесенные к единице измерения количества вещества.

Массовая теплоемкость:

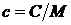. [Дж/кг×К] (2.38)

Объемная теплоемкость

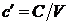. [Дж/м³×К] (2.39)

Мольная теплоемкость

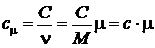. [Дж/моль×К] (2.40)

Между объемной и мольной теплоемкостями существует, очевидная взаимосвязь:

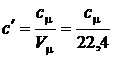. [Дж/м³×К] (2.41)

Аналогично можно записать зависимость, связывающую объемную и удельную (массовую) теплоемкости

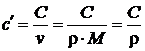или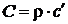

Таким образом, справедливы соотношения:

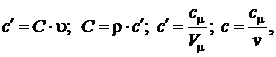
где 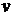– количество вещества (число молей) .

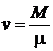Мольная теплоемкость удобна при использовании, т. к. она зависит от особенностей структуры отдельных молекул. Введение ее дает возможность сравнить теплоемкости разных газов, ибо в 1 моле любого вещества при нормальных условиях содержится одно и тоже число молекул: .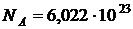

Теплота Q – есть функция процесса, а число всевозможных процессов бесчисленно велико, следовательно, и теплоемкость тела может изменяться неограниченно от 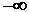до .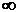

Наиболее часто используются изохорная 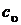и изобарная 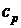теплоемкости. Причем изобарная теплоемкость всегда больше изохорной с_р > с_u на величину тепла, затраченного на совершение работы расширения в изобарном процессе при изменении температуры на 1 К. Рассмотрим систему, содержащую 1 кг вещества.

В соответствии с первым началом термодинамики для изохорного процесса 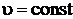, , 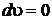следовательно

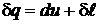
или иначе 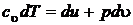, т. к. 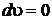, то и

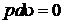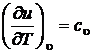или 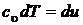. (2.42)

Для изобарного процесса, используя параметр состояния энтальпии, можно также записать 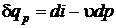, , 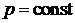, 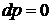следовательно,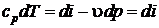

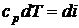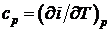, . (2.43)

Уравнение Майера

Найдем зависимость между изобарной и изохорной теплоемкостями.

Воспользуемся первым началом термодинамики

.

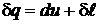Для параметра состояния u, считая независимыми переменными u и T, можно записать выражение полного дифференциала в виде

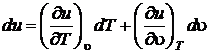. (2.44)

Подставим du в первое начало термодинамики

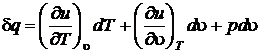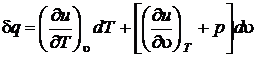или

или

с учетом того, что 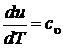, получим .

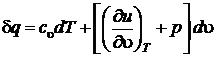Предполагая процесс подвода тепла изобарным, после деления на dT получим

; .

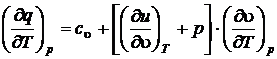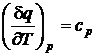Величину 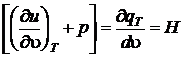принято называть теплотой расширения – количество теплоты необходимое для изотермического увеличения объема тела на единицу объема.

Тогда 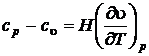. (2.45)

Для твердых и жидких фаз, слабо расширяющихся при нагревании, теплота расширения Н невелика. Мало и изменение объема .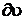

В этом случае 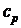практически не отличается от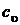

.

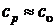Для идеальных газов 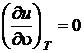. В этом случае уравнение первого начала сводится к виду

.

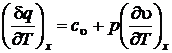Если процесс изобарный .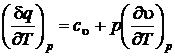

Продифференцируем уравнение состояния идеального газа при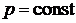

,

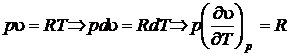тогда после подстановки, получим

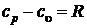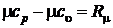, . (2.46)

где 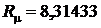– универсальная газовая постоянная, Дж/моль×К; 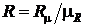– индивидуальная газовая постоянная, Дж/кг×К. Индивидуальная газовая постоянная 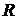практически всегда используется в технических расчетах и в какой то степени она характеризует свойства конкретного газа.