Механическая работа и механическая энергия
При формулировке первого закона необходимо различать энергию, накопленную системой и энергию пересекающую ее границы в процессе совершения термодинамического процесса. Накопленная системой энергия из кинетической, потенциальной и внутренней составляющих является параметром состояния.
Энергия, пересекающая границы системы, не являясь параметром состояния, подразделяется на работу и теплоту. По своей сути они представляют два различных способа передачи энергии через границу системы. Принцип сохранения энергии приводит к необходимости составления энергетического баланса, связывающего энергию, запасенную системой, с энергией переходящей через ее границы в результате совершения процесса по изменению состояния термодинамической системы.
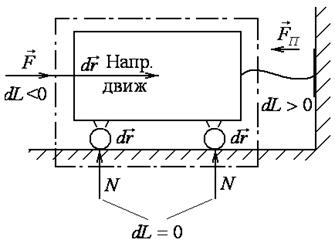 Рисунок 2.1 К расчету механической работы Рисунок 2.1 К расчету механической работы |
Механическая энергия совершается при воздействии силы на подвижные границы системы. При этом работа рассчитывается как скалярное произведение силы на перемещение точки ее приложения в направлении действия силы:
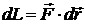 . (2.8)
. (2.8)
или для конечной величины перемещения:
 . (2.9)
. (2.9)
Следуя законам математики модуль (величина скалярного произведения) может быть найден как произведение модуля силы на модуль перемещения и на 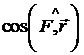 угла между
угла между
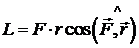 (2.10)
(2.10)
Для вычисления этого интеграла необходимо знать функцию 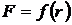 .
.
В термодинамике принято считать работу и энергию, подводимые к системе, положительными, а отводимые от системы – отрицательными.
Кинетическая энергия системы легко рассчитывается при известной массе и скорости по зависимости:
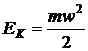 . (2.11)
. (2.11)
По закону сохранения энергии в механике подводимая к системе энергия расходуется на изменение кинетической и потенциальной составляющих энергии системы. Потенциальная энергия системы в поле тяготения определяется положением ее центра масс относительно плоскости нулевого уровня и рассчитывается по известной зависимости:
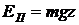 . (2.12)
. (2.12)
Тогда закон сохранения энергии в механике запишется в виде:
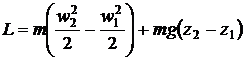 , (2.13)
, (2.13)
или в дифференциальной форме
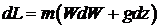 . (2.14)
. (2.14)
Энергия переходит через границы системы только при совершении работы, поэтому работа всегда является функцией процесса.
Работа изменения объема
Если силы действуют перпендикулярно границе термодинамической системы, то это может вызвать перемещение границ системы, а, следовательно, вызвать изменение ее объема.
Чаще всего это можно наблюдать в жидкостях и особенно в газах. Поршень действует на термодинамическую систему с силой (рисунок 2.2)
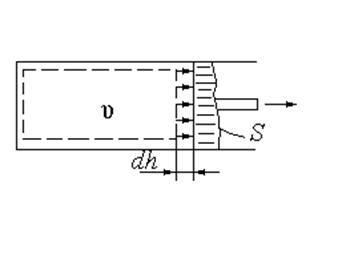 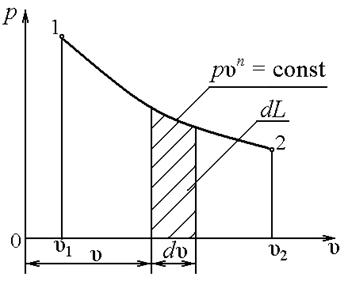 Рисунок 2.2 Рисунок 2.3 Работа расширения Работа расширения в Рисунок 2.2 Рисунок 2.3 Работа расширения Работа расширения в 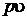 – диаграмме – диаграмме |
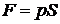 ,
,
где р – давление, Па; S – площадь поршня, м2.
При этом поршень перемещается на величину dh. В этом случае объем системы изменяется на 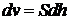 . Работа силы может быть выражена в виде
. Работа силы может быть выражена в виде 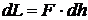 . Подставляя
. Подставляя 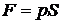 , получим
, получим
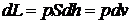 . (2.15)
. (2.15)
Для обратимых процессов вычисление конечной работы достаточно просто.
Конечная работа может быть найдена в этом случае интегрированием
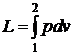 . (2.16)
. (2.16)
Интеграл берется, если известна зависимость 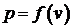 .
.
2.4 р, u – диаграмма
В термодинамике широкое распространение получила р, u – диаграмма, которую еще называют диаграммой работ. Действительно, в этой системе координат удельная работа изображается площадью под кривой процесса 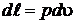 . Удельная работа при конечном изменении параметров системы может быть найдена интегралом
. Удельная работа при конечном изменении параметров системы может быть найдена интегралом
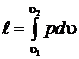 . (2.17)
. (2.17)
Проще всего этот интеграл взять для изобарного процесса. В этом случае 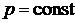 и его можно вынести за знак интеграла
и его можно вынести за знак интеграла
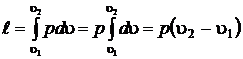 . (2.18)
. (2.18)
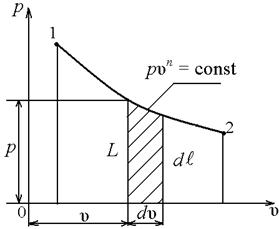 а) работа расширения а) работа расширения 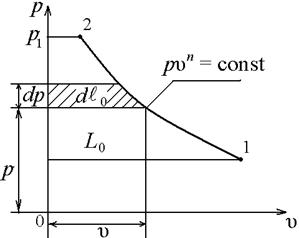 б) располагаемая работа Рисунок 2.4 б) располагаемая работа Рисунок 2.4 |
Если работа совершается термодинамической системой, то она положительна, если работа совершается над системой, то она отрицательна (рисунок 2.4, а).
При изучении термодинамики потока жидкости и лопаточных машин (компрессоров, турбин) большую роль играет располагаемая работа. В компрессоре это работа, затрачиваемая на повышения давления рабочего тела. Если при объеме uизолировать давление на dр, то элементарная работа, затраченная на сжатие составит:
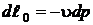 . (2.19)
. (2.19)
Для конечного процесса работа найдется как интеграл:
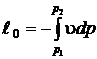 . (2.20)
. (2.20)
В р, u – диаграмме располагаемая техническая работа – 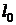 она изображается площадью между кривой процесса и осью давлений (рисунок 2.4,б).
она изображается площадью между кривой процесса и осью давлений (рисунок 2.4,б).
