Определение постоянной ридберга по спектру атомарного водорода

Цель работы – ознакомиться с принципом работы монохроматора. Изучить закономерности в спектре атома водорода. Определить экспериментально постоянную Ридберга

Краткое теоретическое введение

Постановка задачи

Атом любого химического элемента состоит из ядра и электронов, вращающихся вокруг него. Размер атома примерно 10^{-10 м, а ядра до 10-14}-10^{-15 м. Основная масса атома (до 99,95%) приходится на ядро, которое, в свою очередь, состоит из протонов и нейтронов. Заряд протона положителен и по абсолютной величине равен заряду электрона ( 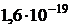Кл). Нейтрон не имеет заряда. Так как число электронов в атоме равно числу протонов в ядре, то атом электронейтрален.}

Простейший атом – атом водорода – состоит из одного протона (ядро) и одного электрона, вращающегося относительно ядра и находящегося на определенном энергетическом уровне, обозначаемом 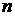. На этом уровне электрон обладает энергией, которая складывается из потенциальной энергии взаимодействия его с ядром (она отрицательна) и кинетической энергии вращения электрона вокруг ядра. Полная энергия электрона в атоме отрицательна, электрон находится как бы в «потенциальной яме» поля ядра, так как при образовании атома потенциальная энергия электрона растет быстрее кинетической.

Совокупность всех значений энергий, которыми может обладать система (атом, например), называется ее энергетическим спектром. Энергетический спектр любого электрона в атоме может иметь строго определенные значения энергии 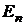. Состояние электрона, в котором реализуется то или иное значение энергии, называется уровнем (n). Уровень, отвечающий состоянию с наименьшим значением энергии, основной, а все остальные уровни – возбужденные.

Закономерности спектра атома водорода впервые были объяснены Н.Бором (постулаты Бора). Находясь в стационарном состоянии, атом не излучает и не поглощает энергию. Атом поглощает или излучает энергию 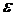в виде кванта (порции) при переходе из одного стационарного состояния (например n₁) в другое (n₂):

,

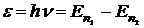откуда

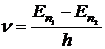, (1)

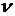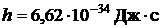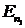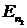где - частота излучаемого кванта, - постоянная Планка, и - соответственно энергии стационарных состояний атома до и после перехода электрона.

Обычно вместо частоты 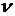рассматривают волновое число 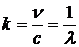, которое показывает, сколько длин волн ( 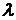) укладывается на единице длины (на 1 м), 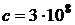м/с – скорость света в вакууме.

В дальнейшем объяснение природы спектров было дано квантовой механикой. Состояние электрона в атоме описывается уравнением Шредингера.

Значение энергии электрона на разрешенном (стационарном) состоянии, даваемое теорией Шредингера, записывается для водородоподобного атома

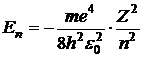, (2)

где 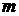- масса электрона, 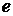- заряд электрона, 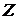- порядковый номер элемента, 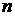- главное квантовое число, определяющее номер уровня, 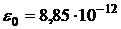Ф/м - электрическая постоянная.

При переходе из одного стационарного состояния ( 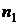) в другое ( 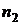) атом излучает или поглощает квант энергии. С учетом (1) частота излучения

,

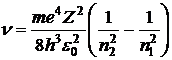а волновое число

.

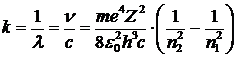Величина

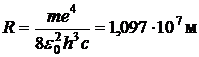
называется постоянной Ридберга. Для водорода 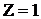, и тогда волновое число

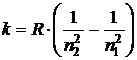. (3)

Из (3) можно получить значение постоянной Ридберга

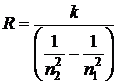. (4)

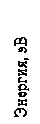Формула (3) называется сериальной. Все описываемые ею спектральные линии могут быть объединены в серии, отличающиеся значением главных квантовых чисел.

В спектре водорода экспериментально изучено шесть таких серий:

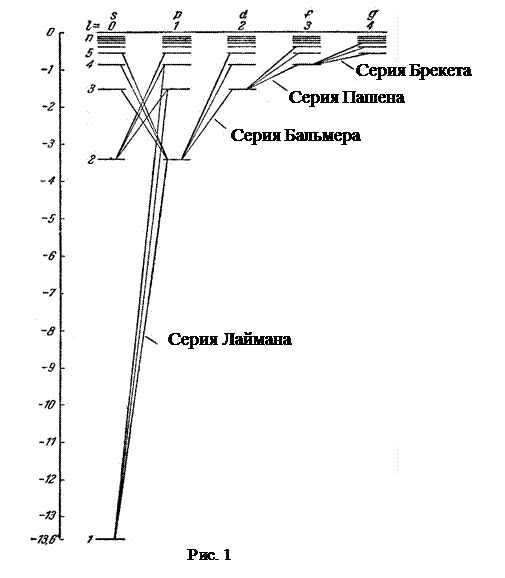
1. Серия Лаймана 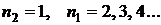Линии этой серии возникают при переходе электронов со всех вышележащих уровней на 1 уровень. Они расположены в ультрафиолетовой области спектра.

2. Серия Бальмера 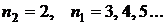Линии этой серии возникают при переходе электронов со всех вышележащих уровней на 2 уровень. Они в основном принадлежат видимой области спектра.

3. Остальные серии лежат в далекой инфракрасной области спектра:

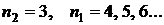- - серия Пашена. Электроны переходят с вышележащих уровней на 3 уровень;

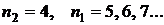- - серия Брэкета. Электроны переходят с вышележащих уровней на 4 уровень;

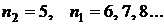- - серия Пфунда. Электроны переходят с вышележащих уровней на 5 уровень;

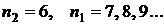- - серия Хэмфри. Электроны переходят с вышележащих уровней на 6 уровень.

Схема энергетических уровней атома водорода приведена на рис.1. Наименьшей возможной энергией атома водорода является энергия – 13,6 эВ (основной уровень). По вертикальной шкале отложены значения энергии, по горизонтальной - указаны состояния с различными значениями орбитального квантового числа. Представлены только разрешенные квантовые переходы, т.е. такие, для которых .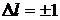

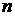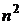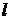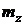Согласно квантовой теории каждому значению , т.е. заданному значению энергии, соответствует различных состояний электрона (различные значения и ), и 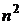называется кратностью вырождения.

В зависимости от значения орбитального числа 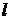принято обозначать следующие состояния электрона:

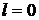s-состояние,

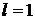p-состояние,

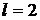d-состояние,

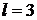f-состояние и т.д.

Постоянную Ридберга можно экспериментально найти с помощью формулы (4). Для этого опытным путем определяются длины волн какой-либо серии. Наиболее удобно это сделать для видимой области спектра, т.е. для серии Бальмера. В настоящей работе определяются длины волн первых четырех наиболее ярких спектральных линий серии Бальмера. В этой серии 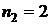, а 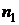принимает значения: 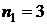(красная линия), 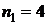(голубая линия), 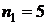(фиолетовая линия), 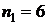(темно-фиолетовая линия, слабо различимая).

Таким образом, постоянная Ридберга определяется из четырех независимых измерений. При правильном выполнении эксперимента, значения 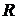получатся близкими (в пределах точности измерений). Это и означает, что линии серии Бальмера подчиняются определенной сериальной закономерности.

Практическая часть

1. Описание установки

В данной работе используется монохроматор УМ-2 и две спектральные лампы - ртутная и водородная. Питание ламп осуществляется от специального устройства.

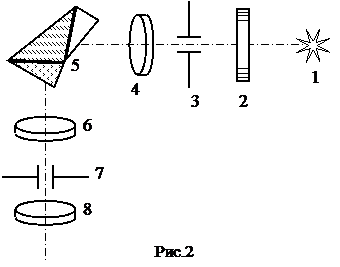Монохроматор УМ-2 используется в данном случае как спектроскоп. Для этого выходная щель монохроматора заменена окуляром, что позволяет наблюдать спектр визуально. Монохроматор служит в работе для определения длин волн линий в спектре водорода. Оптическая схема монохроматора показана на рис. 2: 1-источник света, 2-защитное стекло щели, 3-щель коллиматора, 4-объектив коллиматора, 5-диспергирующая призма, 6-объектив зрительной трубы, 7-указатель в фокальной плоскости окуляра, 8-окуляр зрительной трубы. Объектив коллиматора, в фокусе которого находится щель, образует параллельный пучок света и направляет его на призму 5. Призма преобразует этот пучок в систему параллельных пучков, выходящих за счет дисперсии под различными углами, зависящими от длины волны. Объектив зрительной трубы фокусирует отдельные параллельные пучки и образует в фокальной плоскости совокупность монохроматических цветных изображений входной щели, которые представляют собой спектры, наблюдаемые с помощью окуляра.

Общий вид монохроматора показан на рис. 3: 1-коллиматор (внутри), 2-щель, ширина которой регулируется микрометрическим винтом 3. Винт 4 служит для фокусировки изображения спектральных линий. Поворот призмы 5 осуществляется вращением барабана 6. В зависимости от положения призмы в поле зрения попадает тот или иной участок спектра. На барабане нанесена шкала в от­носительных делениях - градусах поворота самого барабана. Шкала барабана освещается осветителем 7, включение которого производится тумблером 8. В фокальной плоскости окуляра 9 зрительной трубы 10 находится указатель 11 (на рис. 2 указатель 7).

Спектральные лампы.

Ртутная лампа. Для того чтобы привести в соответствие деления шкалы барабана с длинами волн, монохроматор необходимо проградуировать. Для градуировки используется газоразрядная ртутная лампа с линейчатым спектром излучения. Включение лампы производит преподаватель.

Водородная лампа. В качестве источника света, спектр которого изучается в данной работе, применяется газоразрядная водородная трубка Гейслера. Трубка представляет собой Н-образный стеклянный баллон, заполненный водородом при давлении порядка нескольких мм.рт.ст. В колена трубки впаяны электроды, на которые подается переменное напряжение 3000 В. В трубке устанавливается тлеющий разряд. В столбе газового разряда происходит диссоциация молекул водорода, атомы которого, возбуждаясь, излучают характерный для атомарного водорода спектр.

Следует заметить, что молекулы водорода также возбуждаются и излучают спектр. Этот молекулярный спектр имеет гораздо более сложную структуру (так называемый "полосатый" спектр). Но интересующие нас 4 линии серии Бальмера гораздо ярче, чем полосы молекулярного спектра, и легко различимы на его фоне.

1. Порядок выполнения работы и обработка

результатов измерения

Градуировка монохроматора.

1. Установить против щели монохроматора ртутную лампу и обратиться к преподавателю с просьбой о ее включении.

2. Вращая винт 4 и перемещая окуляр 9, получить четкое изображение спектральных линий.

3. Поворачивая барабан 6, совместить изображение спектральной линии с указателем и произвести отсчет делений ( 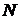) по шкале барабана.

4. Эту операцию произвести для всех линий, указанных в таблице, имеющейся на установке. Линия к указателю подводится со стороны больших длин волн. Для правильной градуировки очень важно производить отсчет делений по шкале барабана именно для тех линий, которые изображены на этой таблице и для которых указана длина волны.

5. Данные занести в табл.1. Для каждой линии отсчет по шкале барабана произвести 3 раза. Выключить ртутную лампу (выполняется преподавателем).

6. Построить на миллиметровой бумаге градуировочный график. График должен быть выполнен очень аккуратно и иметь размер примерно 35х35 см. На график наносить точки, соответствующие средним делениям шкалы барабана.

Таблица 1

Спектр атома ртути

№ п/п	Цвет спектральной линии ртути	Длина волны 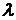, нм	Отсчет по шкале барабана, дел

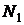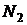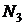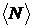Изучение спектра водорода.