Уравнения идеализированного однофазного трансформатора

Рассмотрим сначала идеализированный однофазный трансформатор с магнитопроводом, выполненным из ферромагнитного материала с линейной зависимостью индукции от напряженности магнитного поля

В = μ_r μ₀ H. (7.7)

Так как магнитное поле в магнитопроводе с площадью поперечного сечения S неоднородное, то для упрощения расчетов не будем учитывать неоднородность поля и примем, что индукция и напряженность определяются их значениями на средней магнитной линии длиной l _ср

Электрическая цепь трансформатора с таким магнитопроводом линейная. Следовательно, для ее анализа можно пользоваться комплексным методом.

На рис. 7.5 приведена схема включения идеализированного однофазного трансформатора между источником ЭДС Е и приемником с комплексным сопротивлением нагрузки

Z₂ = z₂ Ðφ₂ (7.8)

Запишем значения ЭДС Е₁ и Е₂, индуктируемых в первичной и вторичной обмотках идеализированного трансформатора магнитным потоком Ф в магнитопроводе по закону электромагнитной индукции в комплексной форме

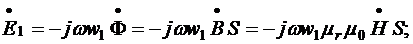(7.9.a)

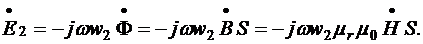(7.9.б)

где В и Н - комплексные значения индукции и напряженности магнитного поля.

При комплексных токах в первичной и вторичной обмотках идеализированного однофазного трансформатора I₁ и I₂ напряженность магнитного поля на средней линии магнитопровода

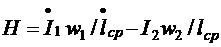(7.10)

По определению ЭДС источника Е =U₁, а ЭДС в обмотках идеализированного трансформатора по второму закону Кирхгофа для контуров, отмеченных на рис. 7.5 штриховой линией, Е₁ = - U₁ и Е₂ = - U₂. Поэтому с учетом (6.1) и (6.2)

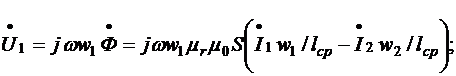(7.11,a)

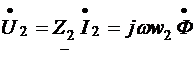(7.11,б)

В частности, в режиме холостого хода трансформатора (цепь вторичной обмотки разомкнута и ток I₂ = 0)

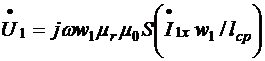(7.11, в)

где I_х - ток холостого хода, или намагничивающий ток.

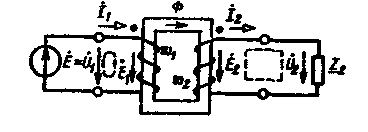
Рис. 7.5

Так как ЭДС источника Е = U₁ является заданной величиной, то по (6.11,а) и (6.11, в)

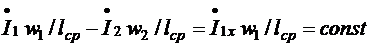(7.12)

Поделив почленно (6.11,б) на (6.11,а), получим

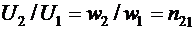(7.13)

- коэффициент трансформации идеализированного однофазного транс­форматора, а подставив комплексное значение магнитного потока Ф в магнитопроводе из (6.11,б) в (6.11,а), получим

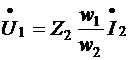(7.14)

Преобразуем выражение (6.14), умножив и разделив его правую часть на w₁/w₂

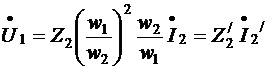(7.15)

Где

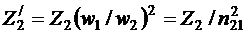(7.16)

- комплексное сопротивление вторичной цепи, приведенное к первичной, или приведенное сопротивление;

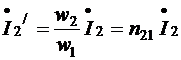(7.17)

- комплексный ток вторичной цепи, приведенный к первичной цепи, или приведенный ток.

Пользуясь понятиями приведенных тока и сопротивления, представим уравнения (6.15) и (6.14) в следующей форме:

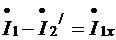(7.18, а)

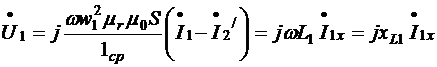(7.18,б)

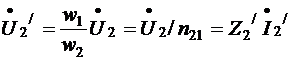(7.18, в)

где

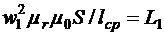(7.19)

- индуктивность первичной обмотки идеализированного однофазного трансформатора; 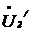— комплексное напряжение вторичной цепи идеализированного однофазного трансформатора, приведенное к первичной цепи, или приведенное напряжение.

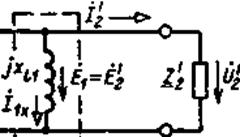
Рис. 7.6

Уравнениям (7.18) соответствует схема замещения цепи, изображенная на рис. 7.6, на которой схема замещения идеализированного трансформатора обведена штриховой линией.

Если относительная проницаемость материала магнитопровода 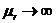, то индуктивное сопротивление становится бесконечно большим, а ток намагничивания I_1х = 0. Идеализированный трансформатор с таким магнитопроводом называется идеальным. При помощи такого трансформатора можно реализовать передачу приемнику максимальной энергии. Действительно, если приемник в цепи подключен через идеальный трансформатор с коэффициентом трансформации

,

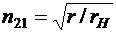то становится r'_н = r, и будет выполняться при любых значениях сопротивлений r и r_н.

При разомкнутой вторичной цепи идеализированный однофазный трансформатор превращается в идеализированную катушку с магнитопроводом. Следовательно, схема замещения ненагруженного идеализи­рованного однофазного трансформатора совпадает со схемой замещения идеализированной катушки, если у катушки и первичной обмотки однофазного трансформатора одинаковые числа витков и магнитопроводы катушки и трансформатора одинаковые.