Алгебраическая форма стехиометрических уравнений

Алгебраическая форма стехиометрических уравнений

Используя алгебраическую форму стехиометрического уравнения, получим такой вид записи соотношения между количествами превратившихся веществ:

(N₁ - N₁₀)/ n₁ = (N₂ - N₂₀)/ n₂ = ..... = (N _i – N _i0)/ n_i = const,

где N₁₀, N₂₀,..., N _i0 - начальные количества компонентов;

N₁, N ₂… N _i - количества компонентов после превращения;

n₁, n₂ ... n_i - соответствующие стехиометрические коэффициенты.

Исходные вещества убывают и для них (N_i - N_i0) < 0, продукты образуются и для них (N_i - N_i0) > 0.

Соответствующий знак имеют стехиометрические коэффициенты n_i:

для исходных веществ (n_i < 0), для продуктов (n_i > 0).

Стехиометрически независимые уравнения

На основании стехиометрической количественной связи между реагентами можно рассчитать состав реакционной смеси в химическом превращении. Таким образом, стехиометрические уравнения служат для составления материальных балансов в химически реагирующей системе и на этой основе- тепловых балансов и расчетов основных технологических показателей, таких как расходный коэффициент, степень превращения, выход продукта, селективность.

Для расчета материальных и тепловых балансов необходимо использовать только стехиометрически независимые уравнения, т.е. Такую систему уравнений, в которой ни одно из них не может быть получено линейной комбинацией других.

Равновесный состав реагирующей смеси

Концентрации всех компонентов в реагирующей смеси связаны между собой стехиометрическим уравнением, их можно определить через начальный состав и степень превращения ключевого компонента x.

В равновесии достигается равновесная степень превращения xр, так что выражение (2) или (3) примет вид

КР = f(xР) (4

Определив из него xр, далее находят равновесные концентрации всех компонентов. Приведем примеры.

Простая реакция.

•Простая обратимая реакция: А = R.

Начальная концентрация компонента А - С_A0, компонент R - отсутствует.

В равновесном состоянии С_А,равн= c_A0(1-x_Р)

и С_R,равн= С_A0x_Р.

Из (2) получим

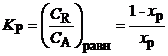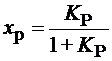, (5)

Учитывая зависимость К_Р(Т) для экзо- и эндотермических реакций, можно построить зависимость x_Р(Т) для этих реакций - рис. 3.3.

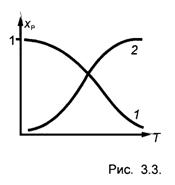
2. Конверсия СО с водяным паром: СО + Н2О = СО2 + Н2. Для нее

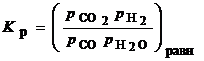
где парциальные давления компонентов pi = РСi;

Р - общее давление.

Концентрации СО, Н₂О, СО₂, Н2 в начальной смеси С₁₀, С₂₀, С₃₀, С₄₀, а в равновесии - С₁р, С₂р, С₃р, С₄р соответственно.

Выразим Сip через равновесную степень превращения xP:

С₁р = С₁₀(1 - x_Р); С₂р = С₂₀ - С₁₀Х_Р; С₃р = С₃₀ + С₁₀X_Р; С₄р = С₄₀ + С₁₀X_Р;

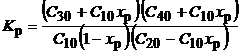
тогда из (3.39) получим квадратное уравнение относительно xP:

Его решение

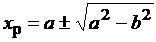
где а = К_Р/[2С₁₀(К_Р - 1)], b = (С₂₀/С₁₀) [К_Р - С₃₀С₄₀/(С₁₀С₂₀)]. (0 < X_Р < 1)

3. Не всегда можно получить аналитическое выражение для xр.

Реакция SO₂ + 0,5O₂ = SO₃ протекает с изменением объема.

Начальные концентрации SO₂ и O₂ - С₁₀ и С₂₀ соответственно.

Парциальные давления компонентов получим из определения pi = РСi

Р - общее давление.

Концентрации компонентов выразим через степень превращения SO₂ - x:

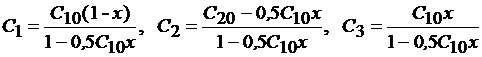
(индекс "3" относится к SO₃).

В условиях равновесия

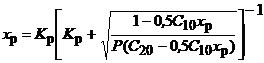
Уравнение решают методом подбора xр, после чего находят концентрации всех компонентов.

Сложная реакция

Для расчета равновесного состава смеси, в которой протекает сложная реакция, описываемая несколькими уравнениями, надо использовать только стехиометрически независимые уравнения как при расчете состава реагирующей смеси .Возможная последовательность расчета такая.

1. Определяется базисная система стехиометрически независимых уравнений, позволяющая выразить концентрации всех компонентов смеси через степени превращения ключевого вещества в каждом уравнении выбранной системы.

Обозначим их C(x). Число определенных степеней превращения и количество уравнений в базисной системе совпадают.

Например, для конверсии метана определена базисная система уравнений

CН4 + Н2О = СО + 3Н2;

СН4 + 2Н2О = СO2 + 4Н2.

и получены выражения для концентраций всех веществ, т.е. C(x).

2. Сложное превращение может быть представлено протекающими реакциями, не обязательно совпадающими с уравнениями для расчета состава реагирующей смеси, но их число такое же, как в базисной системе уравнений. Для этих уравнений известны константы равновесия, и можно определить уравнения равновесия. Обозначим их KPj(C).

В примере конверсии метана такими реакциями являются реакции

CН4 + Н2О = СО + 3Н2;

СО + Н2О = СО2 + Н2,

и химическое равновесие - KP(C) - определяется уравнениями:

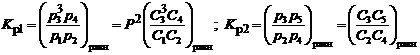
где КР1, КР2 – константы равновесия; р1, р2, р3, р4, р5 – равновесные парциальные давления соответственно CН4, Н2О, Н2, СО, СО2; Сi – соответствующие концентрации (мольные доли).

3. Полученные зависимости C(x) подставляем в выражения K_Pj(C) и получаем зависимости K_Pj(х), в которых x становятся равновесными степенями превращения X_Р, т.е. получаем зависимости K_P(X_Р). Для заданных условий (температура, давление) определяем константы равновесия реакций, и из уравнений K_P(X_Р) определяем все значения X_P. Теперь из имеющихся зависимостей C(x) можно рассчитать равновесный состав реакционной смеси – концентрации всех компонентов.

Изменение химического равновесия достигается изменением внешних условий. Направленность влияния определяется правилом, называемом принципом Ле-Шателье:

Схема превращения.

Кинетика химических реакций описывает, как и с какой скоростью превращаются вещества.

Для предсказания количества оставшихся и образовавшихся компонентов надо иметь стехиометрические уравнения, количество которых определено из условия их независимости. Стехиометрия окисления аммиака представлена двумя уравнениями:

4NH₃ + 5O₂ = 4NO + 6H₂O

(1)

4NH₃ + 3O₂ = 2N₂ + 6H₂O

Если бы имело место только параллельное окисление NH3 до NO и N2, то процесс описывался бы пунктирными линиями на рис. 1: когда весь аммиак окислится, содержание NO и N2 не будет меняться. Реальное изменение концентраций NO и N2 представлено сплошными линиями на рис. 1. Содержание NO сначала растет, а затем уменьшается. Значит, наряду с образованием NO в соответствие с первым уравнением в (1) происходит его дальнейшее превращение. Установлено, что кроме реакций (1) имеют место следующие превращения:

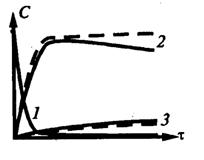2NO = N₂ + O₂ ; 6NO + 4NH₃ = 5N₂ + 6H₂O (2)

Схема превращения показывает реальные взаимодействия между компонентами - пути превращения - в реагирующей системе. Может быть представлена химическими уравнениями протекающих реакций подобно (1)-(2) или графически:

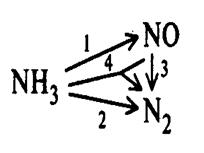
Схема превращения состоит из частных реакций, или этапов. Кинетические уравнения не могут быть записаны произвольно, и их число должно соответствовать реальным путям превращения компонентов.

Схема превращения необходима, чтобы предсказывать изменение содержания веществ в реагирующей системе по мере протекания в ней химических превращений

Кинетическое уравнение.

Кинетическое уравнение, или кинетическая модель, реакции - зависимость скорости реакции от условий ее протекания.

Для элементарной реакции А + B = R + ... , т.е. протекающей в одну стадию, кинетическое уравнение строится на основе закона действующих масс:

r = kCACB,(7)

где k – константа скорости реакции; CA, CB – концентрации компонентов А и В.

Закон действующих масс применим строго только к элементарной реакции, в которой взаимодействие компонентов происходит в одну стадию.

В общем виде кинетическое уравнение будем представлять в виде

r = kf(C), (8)

где f(C) – функция зависимости скорости реакции от концентраций веществ – участников реакции.

При протекании сложной реакции кинетических уравнений вида (8) будет столько, сколько частных реакций с схеме превращения.

В кинетическом уравнении (8) k - константа скорости, зависящая от температуры по уравнению Аррениуса

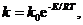(9)

где Е - энергия активации.

Чем больше Е, тем сильнее увеличивается k с температурой.

Кинетическое уравнение вида (8) описывает скорость простой необратимой реакции (или частной реакции в сложной схеме превращения).

Простая обратимая реакция A = R есть фактически сложная реакция, в которой протекают две частные реакции: A превращается в R (прямая реакция) и R превращается в A (обратная реакция). Скорость превращения и, следовательно, скорость реакции r будет равна разности скоростей прямой r1 и обратной r2 реакций: r = r1 - r2 .

Пусть обе реакции первого порядка: r1 = k1CA, r2= k2CR. Тогда

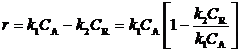В преобразованном уравнении перед квадратной скобкой стоит выражение скорости прямой реакции.

В равновесии концентрации компонентов А и R будут, естественно, равновесными, равными CA.равн и CR,равн, и r = 0. Это возможно, если выражение в квадратных скобках равно нулю, т.е. CR.равн/CA.равн = k1/k2.

Термодинамическое условие равновесия устанавливает связь КP = (CR/CA)равн. Из последних двух уравнений следует связь кинетических (k1, k2) и термодинамического (КP) параметров:

k1/k2 = КP (10)

Зависимости k1, k2, КP от температуры имеют вид

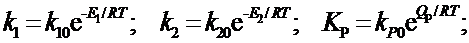Подставив k1 и k2 в (10), получим

QP = E2 - E1 , (11)

т.е. тепловой эффект обратимой реакции равен разности энергий активации обратной и прямой реакций. Это соотношение следует из рассмотрения диаграммы "путь реакции - потенциал реагирующей системы" (рис. 2).

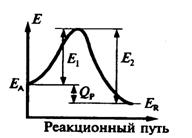
На диаграмме ЕA и ЕR потенциалы исходного вещества А и продукта R. Разность их QP высвобожденная энергия в результате превращения. Для превращения А в R необходимо преодолеть энергетический барьер величиной Е1 (энергия активации прямой реакции). В обратном направлении - величина такого барьера Е2. Разность между ними и дает величину теплового эффекта QP.

Для экзотермической реакции QP > 0 и Е2 > Е1 (как показано на рис. 2). Для эндотермической QP < 0 и Е2< Е1.

Скорость любой обратимой реакции всегда можно представить так:

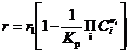(12)

где r1 - скорость реакции в прямом направлении; - выражение закона действующих масс как в уравнении равновесия (12), но концентрации текущие, а не равновесные.

Химические процессы

Химический процесс – явление взаимодействия химической реакции и процессов переноса на молекулярном уровне, которые являются его составляющими.

Группа А (по ф/х признакам, характеризующих протекающую реакцию)

Группа Б ( физические признаки, характеризующие фазовый состав с реагентом)

Группа А:

1. тип химической реакции:

• прямое химическое взаимодействие
• реакция с химическим воздействием (каталитическая реакция)
• реакция с физическим воздействием (под действием света, радиационная реакция, электрохимическая реакция)

1. термодинамические показатели:

а) тепловой эффект:

· экзотермический процесс

· эндотермический процесс

· смешанный ХП

б) направленность превращения:

· обратимые ХП (до Хр)

· необратимые (нет равновесия, не достигается)

· смешанные ХП

1. кинетические характеристики:

а) схема превращения

· простая реакция

· сложная (параллельная, последовательная)

· общий случай

б) кинетическая модель

r = f (С, T)

Группа Б

1.фазовый состав:

а) число участвующих фаз с реагентами:

· гомогенный ХП (все реагенты в одной фазе)

· Гетерогенный (многофазный)

1. состояние фаз

а) газ

б) жидкость

в) твердое

основная цель изучения ХП изучение скорости превращения в нем и влияния на ХП условий протекания.

Гомогенный ХП – процесс протекающий в одной фазе. В этой фазе выровнены все условия протекания реакции во всем выделявшемся объеме.

1. простоя реакция

а) необратимая

Гетерогенный химически процесс – процесс, в котором исходные вещества и в общем случае продолжают находится в разных фазах.

Аг + Втв = Rг + S

Гетерогенные процессы подразделяют:

1. «газ - твердое»

а) адсорбция

б) десорбция

в) обжиг руды

г) окисление Ме

д) горение тв. топлива

1. «газ - жид»

а) адсорбция

б) десорбция

в) дистилляция

г) ректификация (протекает с химическим взаимодействием)

1. «жид - тв»

а) адсорбция

б) десорбция

в) кристаллизация

г) растворение

д) выщелачивание

1. «жид - жид» (несмачивающие)

а) экстракция

б) эмульгирование

1. «тв - тв»

а) процесс спекания (производство цемента)

б) высокотемпературный синтез неорг материала

1. многофазная система.

В гетерогенных ХП реактанты находятся в разных фазах, а реакция протекает либо на границе раздела фаз, либо в одной из фаз.

1. «Газ – тв» («жид - тв»)

Aг + Bт = Rг (модель «сжимающаяся сфера»)

происходит уменьшение размера твердого материала по мере протекания процесса вплоть до его исчезновения

структура процесса:

В газовой фазе:

• I Перенос реагента А из газового потока к поверхности твердой частицы
• II Реакция А с твердым В на наружной поверхности частицы
• Перенос продукта реакции R от поверхности в газовый поток

В твердой фазе:

• II Реакция В с газообразным компонентом А поверхности
• Изменение (уменьшение) размера частицы r

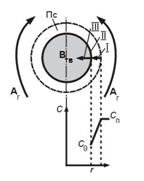
Допущения:

1. тв частица – шарообразной формы.
2. поверхность частицы тв. – равнодоступна, т.е. перенос между потоком и частицей, одинаков по всей поверхности.
3. Т_потока = Т_{частицы}

По мере протекания процесса происходит уменьшение размера тв материала, вплоть до его исчезновения. ( размер = 0, реакция прошла до конца).

Математическая модель:

W_I = W_II

W_I = -bSr(C₀ - C_П)

W_II = -k(C_П)Sr , где: b - коэффициент массообмена, k - константа скорости реакции, Sr – поверхность твердой частицы, tк - время полного превращения, C0 - концентрация А в потоке, R₀ - первонач. радиус частицы, C_П - концентрация А на поверхности, r - радиус частицы.

Наблюдаемая скорость:

Wн=-kCп=-kC0/(1+k/b)=Kн*C0

Наблюдаемая скорость превращения, отнесенная к одной частице:

Wн(част)= WнSr= Wн*4pr2= - 4pR02КНC0r2= -4pR02КНC0(1 - t/tк)2

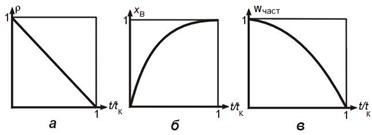
Изменение во времени t безразмерного радиуса частицы r (а), степени превращения твердого реагента xВ (б) и скорости превращения частицы Wн(част) (в) для гетерогенного процесса "сжимающаяся сфера". tк - время полного превращения.

r = 1 - t/tк;

хB = 1 - (1 - t/tк)1/3 ;

Wн(част) = -4pR02КНC0(1 - t/tк)2

Лимитирующие стадии и режимы процесса

· Если k<<b, т.е. реакция малоинтенсивна; C_П~ C₀, Wн=-kС₀ кинетический режим: Химическая реакция – лимитирующая стадия

· Если k>>b, интенсивность массообмена мала; C_П<< C0, Wн=-b С₀ диффузионный режим: массоперенос – лимитирующая стадия

Влияние условий процесса на скорость превращения

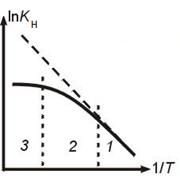
Влияние температуры

Зависимость наблюдаемой константы КН скорости превращения в гетерогенном процессе "сжимающаяся сфера" от температуры Т. Пунктир – k(T).

Режимы процесса:

1 – кинетический (k<<b, Kн=k);

2 - переходный;

3 – диффузионный (k>>b, Kн=b

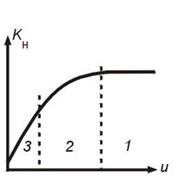
Влияние скорости газового потока

Зависимость скорости обтекания частицы u от температуры Т.

Режимы процесса:

1 – кинетический (при больших скоростях потока с возрастанием b режим не зависит от u);

2 - переходный;

3 – диффузионный

(b << k, Kн=b и увеличивается с увеличением скорости газового потока).

Интенсификация процесса

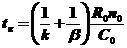
Пути уменьшения tк и, следовательно, интенсификации процесса:

· увеличение концентрации компонента в газе C0;

· дробление частиц - уменьшение R0;

· увеличение температуры и, следовательно, константы скорости k;

· увеличение скорости потока и, следовательно, коэффициента массообмена b.

· Влияние T и u ограничено соответствующим режимом процесса – кинетическим и диффузионным.

2. «газ – жид»

Взаимодействие "газ-жидкость" представлено в промышленности несколькими разновидностями по способу контакта фаз:

• барботаж (диспергированный газ в виде пузырей поднимается в слое жидкости);

• орошение (диспергированная в виде капель жидкость пролетает через газ);

• пленочное течение (жидкость пленкой стекает по поверхности, поток газа проходит вдоль нее);

• контакт в насадочной колонне (близко к пленочному течению - жидкость стекает по насадке в виде нерегулярной, возмущенной пленки, газ проходит в свободном пространстве);

• газо-жидкостной поток (потоки газа и жидкости движутся спутно, в одном направлении).

Применение гетерогенные процессы в системе «газ-жидкость»
широко используются в химической технологии

а) в качестве самостоятельных процессов получения необходимых продуктов

• Абсорбция аммиака растворами азотной кислоты при производстве аммиачной селитры или растворами серной кислоты при производстве сульфата аммония (производство удобрений)

• Хлорирование жидких ароматических углеводородов (органический синтез)

б) в качестве вспомогательных процессов очистки газовых смесей

• Абсорбция углекислого газа водными растворами моноэтаноламинами

• Абсорбция карбоната калия с целью очистки синтез-газа в производстве аммиака

• Абсорбция диоксида серы растворами сульфита и гидросульфита аммония при санитарной очистке газов

Математическая модель

Математическая модель указанной последовательности этапов основана на равенстве потоков W_I, W_II и W_III на стадиях переноса и скорости превращения W_IV компонента А:

W_I = W_II = W_III = W_IV

Перенос через газовый пограничный слой

W_I = -bгS(Р_A* - Р_A), где bг - коэффициент массообмена между газом и поверхностью раздела фаз; Р_A* - парциальное давление А у поверхности раздела фаз; S - величина поверхности раздела фаз.

Перенос через поверхность раздела фаз осуществляется на расстоянии размера молекул, и можно полагать, что приповерхностные парциальное давление в газе Р_A* и концентрация в жидкости С_A* находятся в равновесии

С_A* = KaР_A*, где Ka - константа абсорбции.

Перенос А через пограничный слой жидкости

W_II = -bжS(C_A - С_A*), где bж - коэффициент массообмена между поверхностью раздела фаз и объемом жидкости.

Реакция протекает в объеме жидкости Vж, и скорость превращения А в объеме:

W_IV = -kC_AC_BVж

Приравниваем W_I, W_II и W_IV:

-bгS(Р_A* - Р_A) = -bжS(C_A - С_A*) = - kC_AC_B Vж

Поток через границу раздела фаз заменяется условием фазового равновесия:

С_A* = KaР_A* .

Из трех уравнений:

С_A* = KaР_A*

-bгS(Р_A* - Р_A) = -bжS(C_A - С_A*)

-bжS(C_A - С_A*) = - kC_AC_BVж

можно определить три неизвестные - установившиеся концентрации Р_A*, С_A* и C_A.

С помощью несложных математических преобразований получаем

С_A* = (bжC_A + bгР_A)/(bж + bг/Ka)

Здесь использована удельная поверхность раздела фаз

Sуд = S/Vж,

обычно используемая для характеристики развитости площади контакта жидкости и газа.

Если перенос из одной среды в другую проходит через несколько последовательных этапов, то его интенсивность определяют общим коэффициентом массопереноса между газом и жидкостью b:

1/b = Ka/bг + 1/bж

Аппараты, в которых осуществляются газожидкостные реакции:

1) Насадочный абсорбер

2) Колонна с ситчатыми переточными тарелками

3) Пленочный абсорбер

4) Абсорбер с барботажным слоем

Условия процесса – состояние каждой из фаз и параметры их взаимодействия.

Скорость превращения в гетерогенном химическом процессе, выраженная через условия процесса, есть наблюдаемая скорость превращения.

Лимитирующая стадия – этап многостадийного процесса, характеризующийся максимальной движущей силой или минимальной интенсивностью. Лимитирующая стадия определяет режим, или область протекания процесса.

Каталитический процесс.

Ряд химических превращений требует инициирования, чтобы превращения могли протекать с заметной скоростью. Таким инициатором могут быть химические вещества – катализаторы. Химические процессы с их участием называются каталитическими.

Катализ – явление возбуждения химических реакций специальными веществами – катализаторами. Катализатор многократно вступает в промежуточное химическое взаимодействие с веществами, участвующими в реакции, и восстанавливает свой состав после каждого цикла промежуточных взаимодействий.

Катализ является не только методом ускорения реакций, но и методом управления ими для направленного осуществления тех или иных превращений, в том числе с получением веществ , которых нет в природе.

Катализаторами могут быть элементарные вещества (металлы, активированный уголь), химические соединения (оксиды, сульфиды, хлориды), сложные комплексы и многоатомные молекулы, их смеси. Специфичность катализатора зависит как от его состава и строения, так и от вида химической реакции.

Каталитические реакции можно классифицировать по фазовым признакам: гомогенные, гетерогенные и микрогетерогенные. В гетерогенном катализе реагирующие вещества и катализатор находятся в разных фазах (например, катализатор – твердый, а реагирующие вещества – в газовой фазе).

ХП в непористом зерне

Наряду с катализаторами имеющими пористую структуру используются катализаторы имеющие непористое зерно катализатора. Такие катализаторы часто используются когда реакция быстрая и развивать внутреннюю поверхность не имеет смысла.

Рассмотреть принцип действия непористого катализатора можно на примере окисления аммиака, эта реакция протекает на платиновом катализаторе в виде проволоки, сплетенной в сетку. Реакция протекает на внешней поверхности, где взаимодействуют компоненты из обтекающего непористый катализатор газового потока. Реагенты должны проникнуть через пограничный слой к поверхности твердого тела – катализатора.

Влияние условий процесса

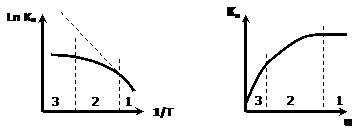Зависимость наблюдаемой константы Кн скорости превращения в гетерогенном процессе

«сжимающаяся сфера» от температуры Т и скорости обтекания частицы u режимы процесса:

1 – кинетический; 2 - переходный; 3 - диффузионный

ХП в пористом катализаторе

Принимаем, что перенос вещества из потока к поверхности катализатора достаточно интенсивен, т.е. концентрация реагентов в потоке и к поверхности одинаковы. Тогда схема процесса следующая. Исходные вещества диффундируют по «порам» катализатора внутрь пористого зерна. Одновременно происходит превращение (протекает каталитическая реакция) на стенках пор. Поскольку размер пор много меньше зерна катализатора, последнее можно представить как квазигомогенное диффузионно-проницаемое тело. Тогда диффузию в нем можно характеризовать эффективным коэффициентом диффузии D_эф , а скорость реакции относить к единице объема зерна катализатора. Предположим, что зерно катализатора – плоское тело толщиной 2R₀ с закрытыми боковыми гранями, так что диффузия протекает только в одном направление, между противоположными гранями. Процесс описывается диффузионным уравнением с источником вещества, записанным для одной половины зерна, поскольку последнее симметрично относительно плоскости симметрии, где находится начальная точка координаты R по толщине зерна:

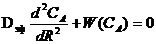
с граничными условиями

dC_A/dR=0 при R=0

C_A=C₀ при R=R₀

Пусть протекает реакция первого порядка, тогда уравнение имеет решение:

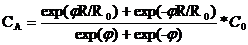
Наблюдаемую скорость превращения определим как среднеинтегральную скорость превращения в пористом зерне, отнесенную к единице объема зерна:

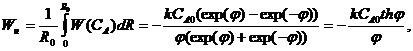здесь

thφ=( 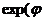) - )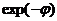/( ) 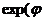+ )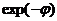, φ=R₀ 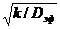- определяющий параметр (модуль Зельдовича-Тиля)

Степень использования внутренней поверхности η – отношение наблюдаемой скорости превращения, определенной при концентрации

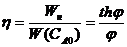
Теория химических реакторов

Химические реакторы.

Изотермические процессы в химических реакторах

Процессы протекающие при постоянной температуре, называются изотермическими процессами. При расчетах ХР, работающих в изотермическом и стационарном режиме, используются балансовые уравнения массы.

Реакторы непрерывного действия (реакторы, работающие в режиме идеального смешения и вытеснения)

РИС

Реактор непрерывного действия работает в режиме идеального смешения, если хим. состав, температура, давление и др параметры, характеризующие свойства реакционной массы, имеют одинаковые значения во всех точках реактора. Уравнение материального баланса для компонента А смеси имеет вид:

(n_A-n_A0)/v_p = W_A

Если объем реакционной смеси не меняется в результате протекающей реакции, то уравнение преобразуется к виду:

(C_A – C_A0)/τ = W_A или C_A0 *(X_A/τ) = -W_A где τ= v_p/V₀ – условное время пребывания смеси в реакторе; С_А – концентрация компонента А в смеси.

РИВ

Реакционная смесь движется в режиме идеального вытеснения, если скорости всех элементов смеси в произвольном сечении реактора равны между собой (поршневой режим), т.е. отсутствует осевое перемешивание, а радиальное перемешивание считается идеальным.

Уравнение материального баланса для модели идеального вытеснения имеет вид:

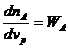, при v_p=0, n_A=n_A0

Если объемный расход реакционной смеси V – величина постоянная, тогда уравнение можно преобразовать к след выражению.

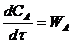, при τ = 0, С_A=С_A0

«исходная модель», в которую входят химические и физические величины и параметры – концентрация, объем реактора, величина потока, коэффициенты переноса и т.д.

«расчетная модель», в которую входят параметры в виде комбинаций первоначальных химических и физических величин. Расчетная модель получена преобразованием исходной модели и используется в программе.

Математические модели процесса в хим реакторе (простая реакция )

Режим процесса	Исходная модель	Расчетная модель
Идеальное смешение, изотермический
Идеальное вытеснение, изотермический
Идеальное смешение, неизотермический
Идеальное вытеснение, неизотермический

Математические модели процесса в хим реакторе (сложная реакция )

Режим процесса	Расчетная модель
Идеальное смешение, изотермический
Идеальное вытеснение, изотермический
Идеальное смешение, неизотермический
Идеальное вытеснение, неизотермический

ХТС представляет собой совокупность аппаратов, машин и др устройств, связанных между собой трубами, газопроводом, электротранспортом результатом которого является получение продукта. Система – совокупность элементов и связей между ними и функций как единое целое. Элемент в системе изменяет свойства входящих в него потоков. В системе можно выделить совокупность аппаратов – подсистему, например, реакторный узел. Отдельный аппарат или подсистему будем называть «расчетным элементом ХТС» или просто элементом. В элемент входят потоки («входные потоки») и выходят из него («выходные потоки»). Расчетным элементом может быть ХТС в целом.

Смеситель. Входят два потока и выходит один. В элементе происходит простое смешение потоков.

Делитель. Входит один и выходят два. Если происходит только разветвление потока, делитель называют простым, - покомпонентный составы входящих и выходящих потоков не меняются. В таких процессах, как испарение, адсорбция, ректификация, фильтрация, составы входящих и выходящих потоков различаются, и такой элемент называют делителем пропорциональным.

Реактор. Проходит один поток, но его компонентный состав принципиально меняется вследствие протекающих в элементе хим превращений.

Классификация элементов ХТС

Проводится по их назначению

- механические и гидродинамические элементы перемещают и изменяют форму и размер материала, объединяют и разделяют потоки эти операции операции осуществляются дробилками, сепараторами, насосами, фильтрами и т.д.

- теплообменные элементы изменяют температуру и теплосодержание потока, переводят вещества в другое фазовое состояние. Для этих целей служат испарители, конденсаторы, сублиматоры.

- массообменные элементы осуществляют межфазный перенос компонентов, изменение компонентного состава потоков без появления новых веществ. Эти операции проводят в дистиллятах, абсорберах, адсорберах, ректификационных колоннах, кристаллизаторах и т.д.

- реакционные элементы реализуют химические превращения кардинально изменяется состав потоков и материала. Эти процессы проходят в реакторах.

- энергетические элементы осуществляют преобразование энергии и получение энергоносителей. К ним относятся турбины, генераторы, привод для выработки механической энергии и др.

Алгебраическая форма стехиометрических уравнений

Используя алгебраическую форму стехиометрического уравнения, получим такой вид записи соотношения между количествами превратившихся веществ:

(N₁ - N₁₀)/ n₁ = (N₂ - N₂₀)/ n₂ = ..... = (N _i – N _i0)/ n_i = const,

где N₁₀, N₂₀,..., N _i0 - начальные количества компонентов;

N₁, N ₂… N _i - количества компонентов после превращения;

n₁, n₂ ... n_i - соответствующие стехиометрические коэффициенты.

Исходные вещества убывают и для них (N_i - N_i0) < 0, продукты образуются и для них (N_i - N_i0) > 0.

Соответствующий знак имеют стехиометрические коэффициенты n_i:

для исходных веществ (n_i < 0), для продуктов (n_i > 0).