Движение тела с переменной массой
Для тела с переменной массой 2-й закон Ньютона:
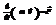
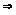
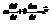 (7)
(7)
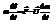 (8)
(8)
Слагаемое –U(dm/dt) 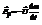 , - реактивная сила она зависит от:
, - реактивная сила она зависит от:
быстроты изменения массы тела dm/dt (в случае присоединения частиц масса тела увеличивается, в случае отделения частиц масса тела уменьшается);
величины и направления скорости U, с которой частицы покидают тело или присоединяются к нему.
Примером реактивной силы может служить сила отдачи при стрельбе из орудия. При отдаче снаряд движется вперед, а орудие откатывается назад. Снаряд и орудие – два взаимодействующих тела. Скорость, которую приобретает орудие при отдаче, зависит только от скорости снаряда и отношения масс снаряда и орудия.
Из уравнения Мещерского следует, что ракета может двигаться и без внешних сил под действием только реактивной силы
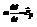 . (10)
. (10)
Вывод формулы Циолковского
Для прямолинейного движения
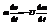
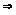
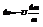
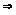
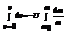
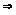
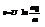
Момент импулься и момент силы.Уравнение моментов.Закон сохранения моментов импульса.Гироскопические явления.
Если на тело действует М(момент силы), то 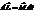 ,
,
L- импульс момента силы. 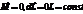 .
.
В замкнутой системе полный момент импульса тела постоянная величина.
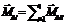
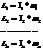 =>
=> 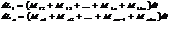
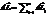
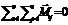
Свободные оси вращения тел.Для любого тела можно выделить 3 оси его вращения. Любое тело обладающее большой массой, способное вращаться относительно одной из своих осей называется гироскоп. Применение гироскопа (самолеты, ракеты корабли)

M=mgl*sin 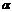 ; M
; M 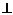 h
h 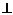 mg;
mg; 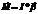 ; Mdt=dL; M и L сонаправлены
; Mdt=dL; M и L сонаправлены 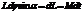
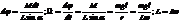
Скорость процессии(поворот вокруг вертикальной оси)
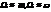
Закон сохранения момента импульса
Если на тело или систему тел не действуют внешние силы (замкнутая система) или момент действующих сил равен нулю, то момент импульса тела сохраняется постоянным как по величине, так и по направлению.
 , при
, при 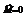
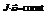 , (15)
, (15)
т.е. момент инерции и угловая скорость обратно пропорциональны: уменьшение момента инерции вызывает увеличение угловой скорости вращения тела и наоборот.
Для системы тел
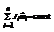 . (16)
. (16)
Пример 1.Гироскопом называется однородное симметричное быстро вращающееся вокруг своей оси симметрии тело. Ось вращения проходит через центр тяжести, поэтому сила тяжести не создает моментов. Из закона сохранения 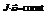 следует сохранение постоянства направления оси гироскопа в пространстве
следует сохранение постоянства направления оси гироскопа в пространстве  .Момент силы, момент импульса, импульс момента силы
.Момент силы, момент импульса, импульс момента силы
Момент силы – это физическая величина, равная произведению силы, приложенной к телу, на плечо этой силы.
Момент силы характеризует способность силы вращать тело вокруг точки, относительно которой он берется.
Моментом испульса частицы А относительно точки О называют вектор М, равнй векторному произведению векторов r и p, где
r – радиус вектор, характеризующий ее положение относительно некоторой точки О выбранной системы отсчета
p – ее импульс в этой системе.
Импульсом момента силы называют величину (интеграл от 0 до t)(Ndt), где N –
момент силы.
