Поток вектора магнитной индукции

Для характеристики магнитного поля вводится понятие магнитного потока. Элементарным магнитным потоком вектора 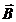сквозь элемент поверхности dS называют физическую величину

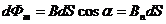, (2.9)

где 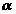- угол между направлением вектора 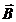и нормалью 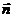к элементу поверхности; 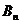- проекция вектора 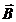на эту нормаль (рис. 2.3).

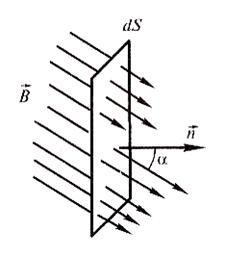
Рис . 2.3

В случае произвольной поверхности S полный поток вектора через неё равен

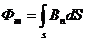= BScos 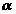(2. 10)

Если поверхность плоская, поле однородно и направлено перпендикулярно поверхности, полный поток равен:

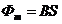(2.11)

Е д и н и ц а Ф - Вб (вебер)

1 Вб-магнитный поток, проходящий через плоскую поверхность площадью 1 м², расположенную перпендикулярно однородному магнитному полю, индукция которого равна 1 Тл. 1 Вб = 1 Тл·м².

Теорема Остроградского-Гаусса для магнитного поля

Поток вектора магнитной индукции сквозь произвольную замкнутую поверхность равен нулю:

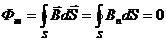. (2.12)

Эта теорема отражает факт отсутствия магнитных зарядов, вследствие чего линии магнитной индукции не имеют ни начала, ни конца и являются замкнутыми. Поэтому магнитное поле является вихревым в отличие от электрического.

Контур с током в магнитном поле

Контур с током, имеющий стороны а и в, помещен в магнитное поле (рис. 2.4).

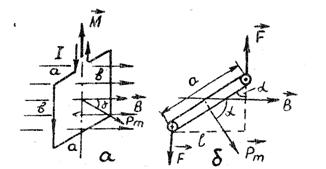
Рис. 2.4

На каждую сторону контура действует сила Ампера. На горизонтальные стороны а контура действуют силы, которые растягивают (или сжимают) контур, не поворачивая его. На каждую из вертикальных сторон в действует сила F. Эти силы создают пару сил с плечом 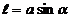и моментом сил

.

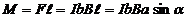Т.к. ab = S – площадь контура, а 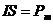- магнитный момент контура, то момент сил примет вид:

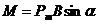(2.13)

Вращающий момент сил 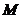, действующий на рамку с током в однородном магнитном поле, пропорционален магнитному моменту 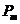контура, индукции 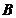магнитного поля и синусу угла между направлением векторов 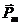и .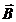

В векторной форме соотношение (2.13) имеет вид

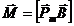(2.14)

Направление 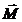определяется по правилу векторного произведения. Вращающий момент сил 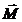направлен перпендикулярно к плоскости, образованной векторам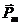и и 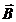, таким образом, чтобы из конца вектора 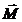кратчайшее вращение от 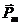к 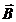происходило против часовой стрелки (рис.2.4).

Е д и н и ц а М - Н · м(ньютон-метр).

Работа по перемещению проводника и контура с током

В магнитном поле

На проводник с током в магнитном поле действует сила, определяемая законом Ампера. Если проводник не закреплён (например, одна из сторон контура изготовлена в виде подвижной перемычки), то под действием силы Ампера он будет в магнитном поле перемещаться. Следовательно, магнитное поле совершает работу по перемещению проводника с током.

Рис. 2.5

Для определения этой работы рассмотрим проводник длиной ℓ с током I (он может свободно перемещаться), помещённый в однородное внешнее магнитное поле, перпендикулярное плоскости контура (рис.2.5). Сила, направление которой определяется по правилу левой руки, а значение - по закону Ампера, равна

F = IBℓ. (2.15)

Под действием этой силы проводник переместится параллельно самому себе на отрезок dx из положения 1 в положение 2. Элементарная работа, совершаемая магнитным полем, равна

δA=Fdx=IBℓdx=IВdS=IdФ ,(2.16)

где ℓdх = dS – площадь, пересекаемая проводником при его перемещении в магнитном поле, BdS = dФ – поток вектора магнитной индукции, пронизывающий эту площадь.

Интегрируя выражение (2.16) найдём работу силы Ампера при конечном перемещении проводника с током в магнитном поле:

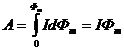, (2.17)

где 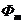- магнитный поток сквозь поверхность, прочерченную проводником, при рассматриваемом перемещении.

Работа по перемещению проводника с током в магнитном поле равна произведению силы тока в проводнике на магнитный поток, пересечённый движущимся проводником. Формула (2.17) справедлива и для произвольного направления вектора .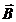

Работа, совершаемая над контуром при его вращении (рис. 2.4), определяется по формуле:

.

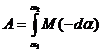Знак «минус» означает, что под действием магнитного поля вращение контура происходит в сторону уменьшения угла от 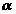до 0. Для однородного магнитного поля (B = const), учитывая формулы (1.1) и (2.13) можно записать:

= = ,

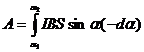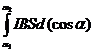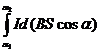С учетом формулы (2.10) работа, совершаемая над контуром с током, вращающимся в однородном магнитном поле, определяется по формуле

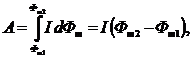(2.18)

где Ф_m и Ф_m – значения магнитного потока через контур соответственно в начальном и конечном его положении.

Работа по перемещению контура с током в магнитном поле равна произведению силы тока в контуре на изменение магнитного потока, сцепленного с контуром.