Принцип суперпозиции (наложения) магнитных полей

Магнитная индукция результирующего поля, создаваемого несколькими токами, равна векторной сумме магнитных индукций (напряженностей) полей, создаваемых каждым током в отдельности:

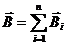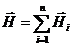(или ), (1.11)

где n – количество элементов тока или проводников с токами.

Применяя закон Био – Савара – Лапласасовместно с принципом суперпозиции можно рассчитать магнитные поля, создаваемые проводниками с током различной формы.

Магнитное поле прямолинейного проводника с током

Определим индукцию (напряженность) магнитного поля прямолинейного проводника с током силой I в произвольной точке М, находящейся на расстоянии 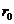от проводника (рис. 1.5).

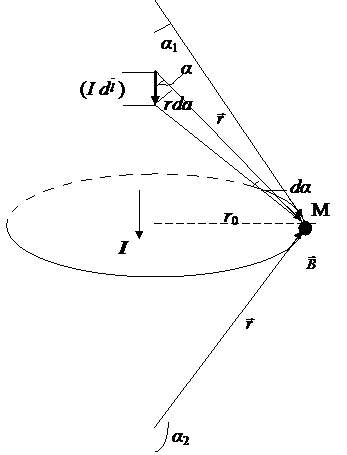Рис.1.5

Выделим на проводнике элемент тока 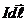и проведем радиус-вектор 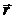в точку М. Векторы 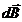( 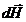) полей всех малых элементов проводника с током ( 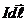) в точке М направлены одинаково перпендикулярно его плоскости (к нам) . Результирующая индукция 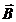(напряженность 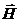) от всех элементов( 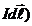направлена в одну сторону и поэтому геометрическое суммирование можно заменить алгебраическим, т.е. интегрированием. В качестве постоянной интегрирования выберем угол α (угол между ( 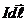) и 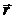), выразив через него переменные r и 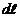, которые входят формулы (1.8) и (1.10). Из рис. 1.5: 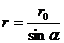, , 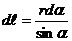подставив r и dl в формулу (1.8) и (1.10), получим

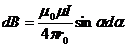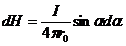; . (1.12)

Угол 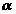для всех элементов прямого проводника изменяется от 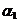до 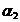(рис.1.5). Проинтегрировав выражение (1.12), определим индукцию 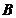(напряженность 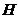) магнитного поля прямого проводника с током I на расстоянии r 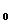от него:

,

.

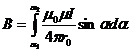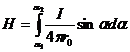Окончательно:

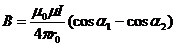(1.13)

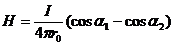. (1.14)

Для проводника бесконечнойдлины при , :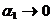

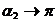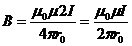(1.15)

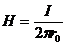. (1.16)

Магнитное поле в центре кругового тока

Как следует из рис.1.6, расстояние от всех элементов I 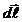кругового тока до центра одинаково и равно его радиусу ( 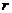= R), а так как все элементы I 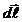перпендикулярны радиусу-вектору 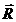, то 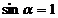. Учитывая это, выражение (1.8) примет вид:

.

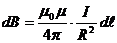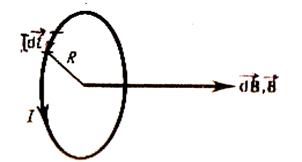
Рис.1.6

Все элементы I 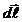создают в центре кругового тока поле одинакового направления: по оси витка перпендикулярно его плоскости. Тогда сложение векторов 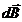можно заменить сложением их модулей (интегрированием по всей длине окружности):

.

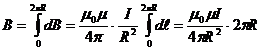Магнитная индукция (напряженность) в центре кругового

витка с током:

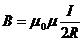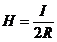; . (1.17)

Магнитная индукция (напряженность) в произвольной точке на оси кругового витка с током:

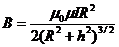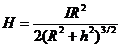; . (1.18)

где h – расстояние от центра витка до произвольной точки на его оси, R – радиус витка.

Закон полного тока

Магнитное поле в отличие от электростатического не потенциальное, а вихревое. Вихревой характер магнитного поля проявляется и при определении циркуляции вектора напряженности поля.

Циркуляцией вектора напряженности магнитного поля 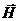по замкнутому кон-туру называется интеграл вида

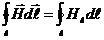(1.19)

где 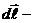вектор элементарной длины контура, направленный вдоль обхода контура, 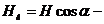составляющая вектора 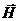в направлении касательной контура, α – угол между векторам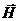и и .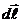

Выберем в магнитном поле бесконечного прямолинейного проводника с током I произвольный контур, совпадающий с одной из силовых линий, охватывающих ток (рис.1.7). Силовые линии прямолинейного проводника, как отмечалось ранее, представляют собой концентрические окружности, плоскости которых перпендикулярны проводнику, а центры лежат на оси проводника.

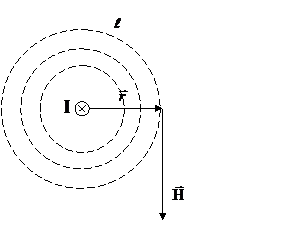
Рис.1.7

В каждой точке этого контура вектор напряженности магнитного поля 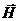одинаков по модулю: 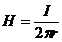, где r -радиус выбранной силовой линии, т.е. окружности. Следовательно, циркуляция вектор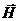а равна

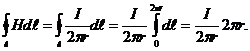
Таким образом, 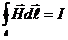(1.20)

Соотношение (1.20), связывающее циркуляцию вектора напряженности магнитного поля и ток, называется законом полного тока.

Если контур охватывает систему токов (рис.1.8),то

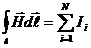(1.21)

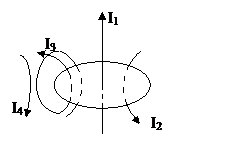
Рис.1.8