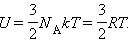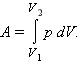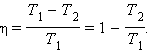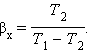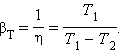Закон Гей-Люссака (закон Шарля)
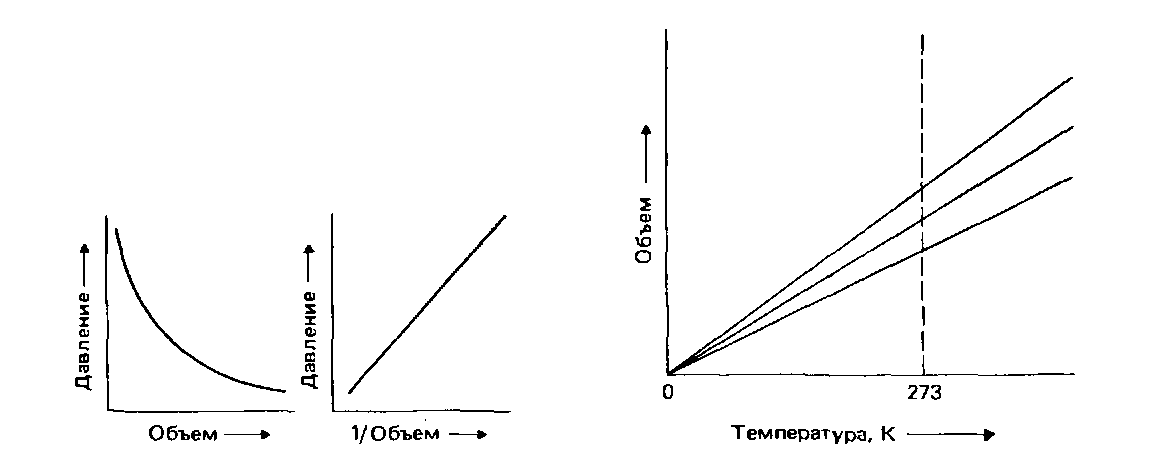
В 1787 г. Шарль показал, что при постоянном давлении объем газа изменяется ( пропорционально его температуре. Эта зависимость представлена в графической форме на рис. 3.3, из которого видно, что объем газа линейно связан с его температурой. В математической форме эта зависимость выражается так:
Закон Шарля чаще записывают в другом виде:
V1IT1 = V2T1 (2)
Закон Шарля усовершенствовал Ж. Гей-Люссак, который в 1802 г. установил, что объем газа при изменении его температуры на 1°С изменяется на 1/273 часть того объема, который он занимал при 0°С. Отсюда следует, что если взять произвольный объем любого газа при 0°С и при постоянном давлении уменьшить его температуру на 273°С, то конечный объем окажется равным нулю. Это соответствует температуре -273°С, или 0 К. Такая температура называется абсолютным нулем. В действительности ее нельзя достичь. На рис. 3.3 показано, как экстраполяция графиков зависимости объема газа от температуры приводит к нулевому объему при 0 К.
Абсолютвый нуль, строго говоря, недостижим. Однако в лабораторных условиях удается достичь температур, отличающихся от абсолютного нуля всего на 0,001 К. При таких температурах беспорядочные движения молекул практически прекращаются. Это приводит к появлению удивительных свойств. Например, металлы, охлажденные до температур, близких к абсолютному нулю, почти полностью утрачивают электрическое сопротивление и становятся сверхпроводящими*. Примером веществ с другими необычными низкотемпературными свойствами является гелий. При температурах, близких к абсолютному нулю, у гелия исчезает вязкость и он становится сверхтекучим.
* В 1987 г. обнаружены вещества (керамика, спеченная из оксидов лантаноидных элементов, бария и меди), которые становятся сверхпроводящими при сравнительно высоких температурах, порядка 100 К (— 173 °С). Эти «высокотемпературные» сверхпроводники открывают большие перспективы в технике.- Прим. перев.
Оглавление:
46.
Одним из важнейших понятий термодинамики является внутренняя энергия тела. Все макроскопические тела обладают энергией, заключенной внутри самих тел. С точки зрения молекулярно-кинетической теории внутренняя энергия вещества складывается из кинетической энергии всех атомов и молекул и потенциальной энергии их взаимодействия друг с другом. В частности, внутренняя энергия идеального газа равна сумме кинетических энергий всех частиц газа, находящихся в непрерывном и беспорядочном тепловом движении. Отсюда вытекает закон Джоуля, подтверждаемый многочисленными экспериментами.
| Внутренняя энергия идеального газа зависит только от его температуры и не зависит от объема |
Молекулярно-кинетическая теория приводит к следующему выражению для внутренней энергии одного моля идеального одноатомного газа (гелий, неон и др.), молекулы которого совершают только поступательное движение:
|
Поскольку потенциальная энергия взаимодействия молекул зависит от расстояния между ними, в общем случае внутренняя энергия U тела зависит наряду с температурой T также и от объема V:
| U = U (T, V). |
Таким образом, внутренняя энергия U тела однозначно определяется макроскопическими параметрами, характеризующими состояние тела. Она не зависит от того, каким путем было реализовано данное состояние. Принято говорить, что внутренняя энергия является функцией состояния.
Внутренняя энергия тела может изменяться, если действующие на него внешние силы совершают работу (положительную или отрицательную). Например, если газ подвергается сжатию в цилиндре под поршнем, то внешние силы совершают над газом некоторую положительную работу A'. В то же время силы давления, действующие со стороны газа на поршень, совершают работу A = –A'. Если объем газа изменился на малую величину ΔV, то газ совершает работу pSΔx = pΔV, где p – давление газа, S – площадь поршня, Δx – его перемещение (рис. 3.8.1). При расширении работа, совершаемая газом, положительна, при сжатии – отрицательна. В общем случае при переходе из некоторого начального состояния (1) в конечное состояние (2) работа газа выражается формулой:
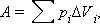 |
или в пределе при ΔVi → 0:
|
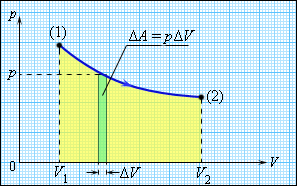 |
| Рисунок 3.8.1. Работа газа при расширении |
Работа численно равна площади под графиком процесса на диаграмме (p, V). Величина работы зависит от того, каким путем совершался переход из начального состояния в конечное. На рис. 3.8.2 изображены три различных процесса, переводящих газ из состояния (1) в состояние (2). Во всех трех случаях газ совершает различную работу.
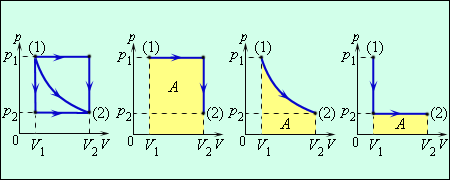 |
| Рисунок 3.8.2. Три различных пути перехода из состояния (1) в состояние (2). Во всех трех случаях газ совершает разную работу, равную площади под графиком процесса |
Процессы, изображенные на рис. 3.8.2, можно провести и в обратном направлении; тогда работа A просто изменит знак на противоположный. Процессы такого рода, которые можно проводить в обоих направлениях, называются обратимыми (см. §3.12).
В отличие от газа, жидкости и твердые тела мало изменяют свой объем, так что во многих случаях работой, совершаемой при расширении или сжатии, можно пренебречь. Однако, внутренняя энергия жидких и твердых тел также может изменяться в результате совершения работы. При механической обработке деталей (например, при сверлении) они нагреваются. Это означает, что изменяется их внутренняя энергия. Другим примером может служить опыт Джоуля (1843 г.) по определению механического эквивалента теплоты (рис. 3.8.3). При вращении вертушки, погруженной в жидкость, внешние силы совершают положительную работу (A' > 0); при этом жидкость из-за наличия сил внутреннего трения нагревается, т. е. увеличивается ее внутренняя энергия. В этих двух примерах процессы не могут быть проведены в противоположном направлении. Такие процессы называются необратимыми.
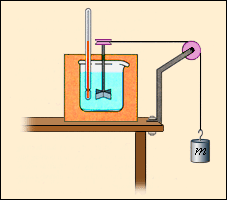 |
| Рисунок 3.8.3. Упрощенная схема опыта Джоуля по определению механического эквивалента теплоты |
Внутренняя энергия тела может изменяться не только в результате совершаемой работы, но и вследствие теплообмена. При тепловом контакте тел внутренняя энергия одного из них может увеличиваться, а другого – уменьшаться. В этом случае говорят о тепловом потоке от одного тела к другому. Количеством теплоты Q, полученным телом, называют изменение внутренней энергии тела в результате теплообмена.

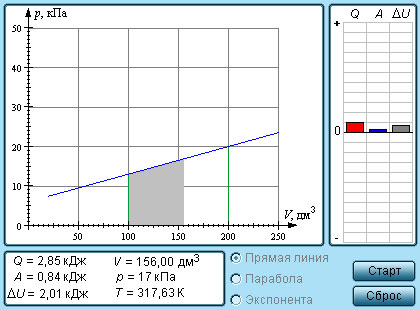 |
| Модель. Работа газа |
Передача энергии от одного тела другому в форме тепла может происходить только при наличии разности температур между ними.
Тепловой поток всегда направлен от горячего тела к холодному.
Количество теплоты Q является энергетической величиной. В СИ количество теплоты измеряется в единицах механической работы – джоулях (Дж).
47.
Q- энергия, которую тело теряет или приобретает при передаче тепла.
Формула количества теплоты зависит от протекающего процесса.
Формулы количества теплоты при некоторых процессах:
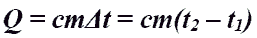 Количество теплоты при нагревании и охлаждении.
Количество теплоты при нагревании и охлаждении.
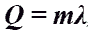 Количество теплоты при плавлении или кристаллизации.
Количество теплоты при плавлении или кристаллизации.
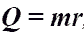 Количество теплоты при кипении, испарении жидкости и конденсации пара.
Количество теплоты при кипении, испарении жидкости и конденсации пара.
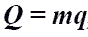 Количество теплоты при сгорании топлива.
Количество теплоты при сгорании топлива.
Дополнительно см. интерактивную презентацию "Фазовые переходы".
Количество теплоты всегда передается от более горячихтел к более холодным до достижения ими одинаковой температуры (теплового равновесия), если нет иных процессов, кроме теплопередачи.
В замкнутой системе тел выполняется уравнение теплового балланса: Q1 + Q2 + ... = 0 - количество теплоты, которое теряют горячие тела, равно количеству тепла, получаемому холодными.
Полезные формулы:
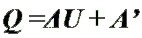 Количество теплоты, переданное телу,
Количество теплоты, переданное телу,
идет на изменение его внутренней энергии
и на совершение им работы (Первый закон термодинамики).
Закон Джоуля-Ленца:в неподвижном металлическом проводнике вся энергия электрического тока превращается в тепло:
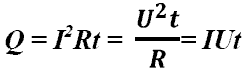 - закон Джоуля - Ленца.
- закон Джоуля - Ленца.
48.
Кипение — это интенсивный переход жидкости в пар, происходящий с образованием пузырьков пара по всему объему жидкости при определенной температуре.
В отличие от испарения, которое происходит при любой температуре жидкости, другой вид парообразования — кипение — возможен лишь при совершенно определенной (при данном давлении) температуре — температуре кипения.
При нагревании воды в открытом стеклянном сосуде можно увидеть, что по мере увеличения температуры стенки и дно сосуда покрываются мелкими пузырьками. Они образуются в результате расширения мельчайших пузырьков воздуха, которые существуют в углублениях и микротрещинах не полностью смачиваемых стенок сосуда.
Пары жидкости, которые находятся внутри пузырьков, являются насыщенными. С ростом температуры давление насыщенных паров возрастает, и пузырьки увеличиваются в размерах. С увеличением объема пузырьков растет и действующая на них выталкивающая (архимедова) сила. Под действием этой силы наиболее крупные пузырьки отрываются от стенок сосуда и поднимаются вверх. Если верхние слои воды еще не успели нагреться до 100 °С, то в такой (более холодной) воде часть водяного пара внутри пузырьков конденсируется и уходит в воду; пузырьки при этом сокращаются в размерах, и сила тяжести заставляет их снова опускаться вниз. Здесь они опять увеличиваются и вновь начинают всплывать вверх. Попеременное увеличение и уменьшение пузырьков внутри воды сопровождается возникновением в ней характерных звуковых волн: закипающая вода шумит.
Когда вся вода прогреется до 100 °С, поднявшиеся вверх пузырьки уже не сокращаются в размерах, а лопаются на поверхности воды, выбрасывая пар наружу. Возникает характерное бульканье — вода кипит.
Кипение начинается после того, как давление насыщенного пара внутри пузырьков сравнивается с давлением в окружающей жидкости.
Во время кипения температура жидкости и пара над ней не меняется. Она сохраняется неизменной до тех пор, пока вся жидкость не выкипит. Это происходит потому, что вся подводимая к жидкости энергия уходит на превращение ее в пар.
Температура, при которой кипит жидкость, называется температурой кипения.
Температура кипения зависит от давления, оказываемого на свободную поверхность жидкости. Это объясняется зависимостью давления насыщенного пара от температуры. Пузырек пара растет, пока давление насыщенного пара внутри него немного превосходит давление в жидкости, которое складывается из внешнего давления и гидростатического давления столба жидкости.
Чем больше внешнее давление, тем больше температура кипения.
Всем известно, что вода кипит при температуре 100 ºC. Но не следует забывать, что это справедливо лишь при нормальном атмосферном давлении (примерно 101 кПа). При увеличении давления температура кипения воды возрастает. Так, например, в кастрюлях-скороварках пищу варят под давлением около 200 кПа. Температура кипения воды при этом достигает 120°С. В воде такой температуры процесс варки происходит значительно быстрее, чем в обычном кипятке. Этим и объясняется название «скороварка».
И наоборот, уменьшая внешнее давление, мы тем самым понижаем температуру кипения. Например, в горных районах (на высоте 3 км, где давление составляет 70 кПа) вода кипит при температуре 90 °С. Поэтому жителям этих районов, использующим такой кипяток, требуется значительно больше времени для приготовления пищи, чем жителям равнин. А сварить в этом кипятке, например, куриное яйцо вообще невозможно, так как при температуре ниже 100 °С белок не сворачивается.
У каждой жидкости своя температура кипения, которая зависит от давления насыщенного пара. Чем выше давление насыщенного пара, тем ниже температура кипения соответствующей жидкости, т. к. при меньших температурах давление насыщенного пара становится равным атмосферному. Например, при температуре кипения 100 °С давление насыщенных паров воды равно 101 325 Па (760 мм рт. ст.), а паров ртути — всего лишь 117 Па (0,88 мм рт. ст.). Кипит ртуть при 357°С при нормальном давлении.
49.
Насыщенный парнаходится в динамическом равновесии со своей жидкостью. Это состояние характеризуется тем, что число молекул, покидающих поверхность жидкости, равно в среднем числу молекул пара, возвращающихся в жидкость за то же время. Название пара — насыщенный — подчеркивает, что при данной температуре в данном объеме не может находиться большее количество пара. Если пар еще не достиг состояния динамического равновесия сжидкостью, он называется ненасыщенным.
Для насыщенного пара характерны следующие свойства:
— при постоянной температуре давление насыщенного пара не зависит от занимаемого объема;
— давление насыщенного пара при постоянном объеме увеличивается с ростом температуры., причем быстрее, чем у идеального газа при тех же условиях.
Как известно, в состав атмосферного воздуха входит и водяной пар. Количество водяного пара (в граммах), содержащееся в 1 м3 воздуха, называется абсолютной влажностьювоздуха. Эта величина не позволяет судить о том, насколько водяной пар в данных условиях близок к насыщению. По этой причине используют понятие относительнойвлажности воздуха, которая равна отношению парциального давления р водяного пара, содержащегося в воздухе при данной температуре, к давлению насыщенного пара р0 при той же температуре (в процентах):
?=р/р0*100%
Температуру, при которой относительная влажность достигает значения 100%, называют точкой росы.Если температура станет хоть немного ниже точки росы, пар начнет конденсироваться: появятся роса, туман.
На практике влажность воздуха определяют, например, с помощью психрометров. Психрометр состоит из двух термометров, один из которых остается сухим, а резервуар другого увлажнен. По разности показаний термометров с помощью таблиц и находят влажность при данной температуре.
Для человека наиболее благоприятна относительная влажность 40—60%.
50.
В 1824 году французский инженер С. Карно рассмотрел круговой процесс, состоящий из двух изотерм и двух адиабат, который сыграл важную роль в развитии учения о тепловых процессах. Он называется циклом Карно (рис. 3.11.4).
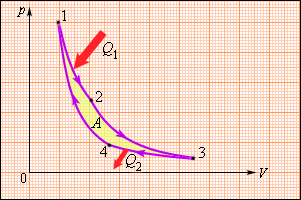 |
| Рисунок 3.11.4. Цикл Карно |
Цикл Карно совершает газ, находящийся в цилиндре под поршнем. На изотермическом участке (1–2) газ приводится в тепловой контакт с горячим тепловым резервуаром (нагревателем), имеющим температуру T1. Газ изотермически расширяется, совершая работу A12, при этом к газу подводится некоторое количество теплоты Q1 = A12. Далее на адиабатическом участке (2–3) газ помещается в адиабатическую оболочку и продолжает расширяться в отсутствие теплообмена. На этом участке газ совершает работу A23 > 0. Температура газа при адиабатическом расширении падает до значения T2. На следующем изотермическом участке (3–4) газ приводится в тепловой контакт с холодным тепловым резервуаром (холодильником) при температуре T2 < T1. Происходит процесс изотермического сжатия. Газ совершает работу A34 < 0 и отдает тепло Q2 < 0, равное произведенной работе A34. Внутренняя энергия газа не изменяется. Наконец, на последнем участке адиабатического сжатия газ вновь помещается в адиабатическую оболочку. При сжатии температура газа повышается до значения T1, газ совершает работу A41 < 0. Полная работа A, совершаемая газом за цикл, равна сумме работ на отдельных участках:
| A = A12 + A23 + A34 + A41. |
На диаграмме (p, V) эта работа равна площади цикла.
Процессы на всех участках цикла Карно предполагаются квазистатическими. В частности, оба изотермических участка (1–2 и 3–4) проводятся при бесконечно малой разности температур между рабочим телом (газом) и тепловым резервуаром (нагревателем или холодильником).
Как следует из первого закона термодинамики, работа газа при адиабатическом расширении (или сжатии) равна убыли ΔU его внутренней энергии. Для 1 моля газа
| A = –ΔU = –CV (T2 – T1), |
где T1 и T2 – начальная и конечная температуры газа.
Отсюда следует, что работы, совершенные газом на двух адиабатических участках цикла Карно, одинаковы по модулю и противоположны по знакам
| A23 = –A41. |
По определению, коэффициент полезного действия η цикла Карно есть
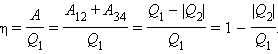 |
С. Карно выразил коэффициент полезного действия цикла через температуры нагревателя T1 и холодильника T2:
|
Цикл Карно замечателен тем, что на всех его участках отсутствует соприкосновение тел с различными температурами. Любое состояние рабочего тела (газа) на цикле является квазиравновесным, т. е. бесконечно близким к состоянию теплового равновесия с окружающими телами (тепловыми резервуарами или термостатами). Цикл Карно исключает теплообмен при конечной разности температур рабочего тела и окружающей среды (термостатов), когда тепло может передаваться без совершения работы. Поэтому цикл Карно – наиболее эффективный круговой процесс из всех возможных при заданных температурах нагревателя и холодильника:
|

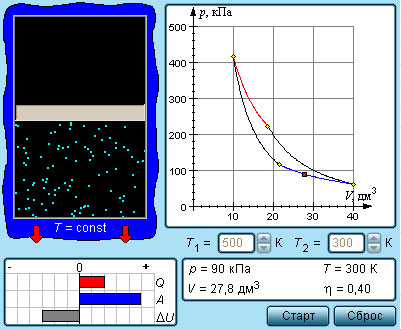 |
| Модель. Цикл Карно |
Любой участок цикла Карно и весь цикл в целом может быть пройден в обоих направлениях. Обход цикла по часовой стрелке соответствует тепловому двигателю, когда полученное рабочим телом тепло частично превращается в полезную работу. Обход против часовой стрелки соответствует холодильной машине, когда некоторое количество теплоты отбирается от холодного резервуара и передается горячему резервуару за счет совершения внешней работы. Поэтому идеальное устройство, работающее по циклу Карно, называют обратимой тепловой машиной.
В реальных холодильных машинах используются различные циклические процессы. Все холодильные циклы на диаграмме (p, V) обходятся против часовой стрелки. Энергетическая схема холодильной машины представлена на рис. 3.11.5.
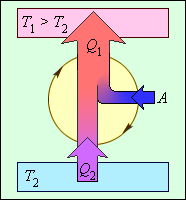 |
| Рисунок 3.11.5. Энергетическая схема холодильной машины. Q1 < 0, A < 0, Q2 > 0, T1 > T2 |
Устройство, работающее по холодильному циклу, может иметь двоякое предназначение. Если полезным эффектом является отбор некоторого количества тепла |Q2| от охлаждаемых тел (например, от продуктов в камере холодильника), то такое устройство является обычным холодильником. Эффективность работы холодильника можно охарактеризовать отношением
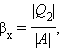 |
т. е. эфективность работы холодильника – это количество тепла, отбираемого от охлаждаемых тел на 1 джоуль затраченной работы. При таком определении βх может быть и больше, и меньше единицы. Для обращенного цикла Карно
|
Если полезным эффектом является передача некоторого количества тепла |Q1| нагреваемым телам (например, воздуху в помещении), то такое устройство называется тепловым насосом. Эффективность βТтеплового насоса может быть определена как отношение
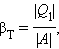 |
т. е. количеством теплоты, передаваемым более теплым телам на 1 джоуль затраченной работы. Из первого закона термодинамики следует:
| |Q1| > |A|, |
следовательно, βТ всегда больше единицы. Для обращенного цикла Карно
|
51.
1. Первый закон термодинамики, установленный на основании многочисленных опытов, утверждает, что изменение внутренней энергии ΔU системы равно сумме совершаемой над системой работы A' внешних сил и количества теплоты Q, переданного системе извне.
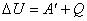 . . | (4.18) |
Этот закон можно сформулировать несколько иначе, если вместо работы A' внешних сил говорить о работе A самой системы. Поскольку A' = – A, то
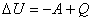 , или , или 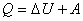 , , | (4.19) |
таким образом, полученное системой количество теплоты равно сумме изменения ее внутренней энергии и работы, совершаемой системой над внешними телами.
Соотношения (4.18) и (4.19) представляют собой математическое выражение первого закона термодинамики, который является конкретной формулировкой закона сохранения энергии применительно к тепловым процессам.
По сути дела, формулировка 1-го начала термодинамики послужила основанием для утверждения в физике понятия "энергия". С той поры оно заняло центральное место в физике, отодвинув на второй план введенное Ньютоном понятие "сила". Признание энергии как наиболее общего понятия, позволяющего рассматривать с единой точки зрения все явления и процессы, следует признать основным достижением науки XIX в.
Весь производственный и научный опыт, многочисленные экспериментальные подтверждения предсказаний, сделанные на основе первого начала, свидетельствуют о справедливости этого базового закона природы.
2. Рассмотрим систему, которая получает энергию в процессе теплообмена. Пусть для изменения температуры системы на ΔT потребовалось количество теплоты Q. Теплоемкостью системы называется величина
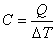 . . | (4.20) |
Если в качестве системы рассматривать 1 моль вещества, то теплоемкость, определяемая соотношением (4.20), называется молярной теплоемкостью. Удельная теплоемкость (теплоемкость единицы массы вещества) связана с молярной теплоемкостью очевидным равенством:
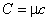 . . | (4.21) |
В уравнении (4.19) величина A, как было показано выше, является функцией процесса, тогда и величина Q, очевидно, зависит от условий процесса и является его функцией. Поскольку Q есть функция процесса, то и теплоемкость, естественно, есть функция процесса и для ее определения необходимо указать условия процесса. Обычно различают теплоемкость при постоянном объеме СV (изохорный процесс) и теплоемкость при постоянном давлении СР (изобарный процесс). Воспользуемся уравнением (4.19) для определения величин СР и СV и установления соотношения между ними.
При изохорном процессе 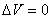 и, как следует из (4.16), работа равна нулю. При этом условии, используя (4.19) и (4.20), находим
и, как следует из (4.16), работа равна нулю. При этом условии, используя (4.19) и (4.20), находим
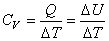 . . | (4.22) |
Для изобарного процесса, используя равенства (4.16), (4.19) и (4.22), получаем
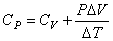 . . | (4.23) |
Уравнение (4.23) показывает, что теплоемкость СР больше СV на величину работы, совершаемой системой при ее изобарном нагревании на 1ºС.
Для моля идеального газа уравнение состояния имеет вид:
| PV = RT. |
Применение этого уравнения к двум состояниям моля газа в изобарном процессе приводит к соотношению
| РΔV = RΔT. | (4.24) |
Подставляя (4.24) в (4.23), получаем
| CP = CV + R. | (4.25) |
Полученное уравнение называется уравнением Роберта Майера. Из сравнения уравнений (4.23) и (4.25) легко вскрыть физический смысл универсальной газовой постоянной. Эта величина, очевидно, равна работе изобарического расширения моля идеального газа при его нагревании на один Кельвин.
52.
Определение. Влажность воздуха – содержание в воздухе водяного пара.
Возникает вопрос, почему же понятие влажности является важным для рассмотрения, и каким образом водяные пары попадают в воздух? Известно, что большую часть поверхности Земли занимает вода (Мировой океан), с поверхности которой непрерывно происходит испарение (рис. 1). Безусловно, в различных климатических зонах интенсивность этого процесса различна, что зависит от среднесуточной температуры, наличия ветров и т. п. Эти факторы обуславливают тот факт, что в определенных местах процесс парообразования воды более интенсивен, чем ее конденсация, а в некоторых – наоборот. В среднем же, можно утверждать, что пар, который образуется в воздухе, не является насыщенным, и его свойства необходимо уметь описывать.
Рис. 1. (Источник)
Для человека величина влажности является очень важным параметром окружающей среды, т. к. наш организм очень активно реагирует на ее изменения. Например, такой механизм регуляции функционирования организма, как потоотделение, напрямую взаимосвязан с температурой и влажностью окружающей среды: при высокой влажности процессы испарения влаги с поверхности кожи практически компенсируются процессами ее конденсации и нарушается отвод тепла от организма, что приводит к нарушениям терморегуляции; при низкой влажности процессы испарения влаги превалируют над процессами конденсации и организм теряет слишком много жидкости, что может привести к обезвоживанию.
Величина влажности важна не только для человека и других живых организмов, но и для протекания технологических процессов. Например, из-за известного свойства воды проводить электрический ток, ее содержание в воздухе может серьезно влиять на корректную работу большинства электроприборов.
Кроме того, понятие влажности является важнейшим критерием оценивания погодных условий, что всем известно из прогнозов погоды. Стоит отметить, что если сравнивать влажность в различные времена года в привычных для нас климатических условиях, то она выше летом и ниже зимой, что связано, в частности, с интенсивностью процессов испарения при различных температурах.