Вынужденные колебания. Резонанс

Вынужденные колебания являются незатухающими. Поэтому необходимо восполнять потери энергии за каждый период колебаний. Для этого необходимо воздействовать на колеблющееся тело периодически изменяющейся силой. Вынужденные колебания совершаются с частотой, равной частоте изменения внешней силы.

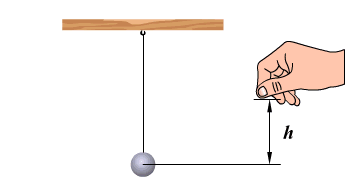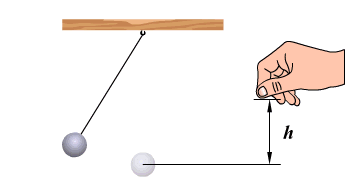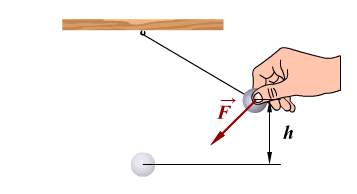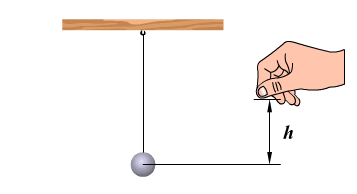
Вынужденные колебания

Амплитуда вынужденных механических колебаний достигает наибольшего значения в том случае, если частота вынуждающей силы совпадает с частотой колебательной системы. Это явление называется резонансом.

Например, если периодически дергать шнур в такт его собственным колебаниям, то мы заметим увеличение амплитуды его колебаний.

21.

Рассмотрим простой маятник — шарик, подвешенный на длинной прочной нити. Такой маятник называется физическим. Если размеры шарика много меньше длины нити, то этими размерами можно пренебречь и рассматривать шарик как материальную точку. Растяжением нити также можно пренебречь, так как оно очень мало. Если масса нити во много раз меньше массы шарика, то массой нити также можно пренебречь. В этом случае мы получаем модель маятника, которая называется математическим маятником.

ОПРЕДЕЛЕНИЕ

Математическим маятником называется материальная точка массой m, подвешенная на невесомой нерастяжимой нити длиной L в поле силы тяжести (или других сил).

Галилео Галилей экспериментально установил, что период колебаний математического маятника в поле силы тяжести не зависит от его массы и амплитуды колебаний (угла начального отклонения). Он установил также, что период колебаний прямо пропорционален L.

Период малых колебаний математического маятника в поле силы тяжести Земли определяется по формуле Гюйгенса:

T=2πLg.

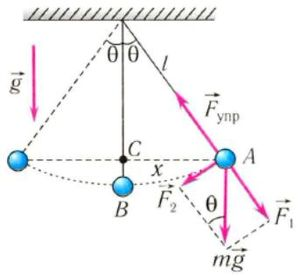
При углах отклонения математического маятника α<200 погрешность расчета периода по формуле Гюйгенса не превышает 1%.

В общем случае, когда маятник находится в однородных полях нескольких сил, то для определения периода колебаний следует ввести «эффективное ускорение» g∗, характеризующее результирующее действие этих полей, и период колебаний маятника будет определяться по формуле

T=2πLg∗.

ОПРЕДЕЛЕНИЕ

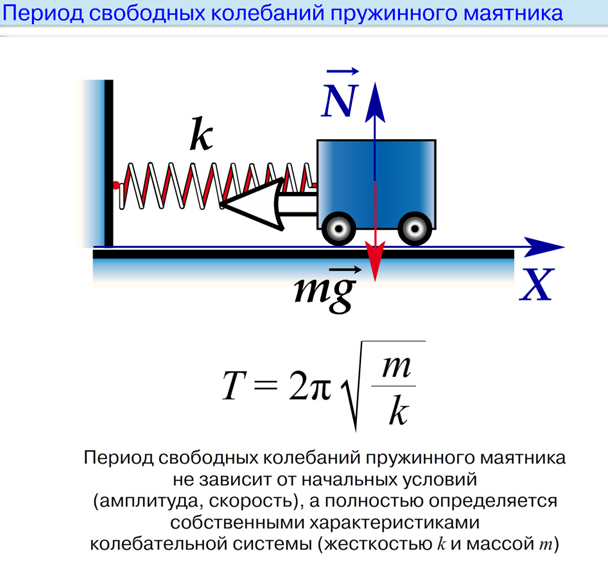
Пружинный маятник − это колебательная система, состоящая из материальной точки массой m и пружины.

Период колебаний пружинного маятника можно найти по формуле

T=2πmk,

где k — коэффициент жесткости пружины маятника. Как следует из данной формулы, период колебаний пружинного маятника не зависит от амплитуды колебаний (в пределах выполнимости закона Гука).

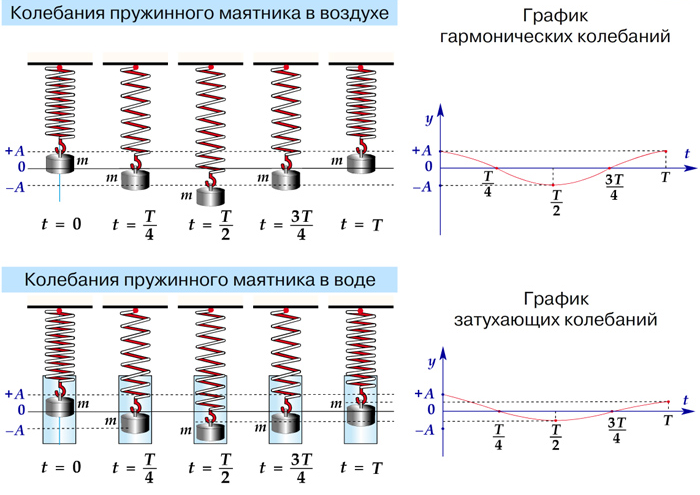
Физи́ческий ма́ятник — осциллятор, представляющий собой твёрдое тело, совершающее колебания в поле каких-либо сил относительно точки, не являющейся центром масс этого тела, или неподвижной оси, перпендикулярной направлению действия сил и не проходящей через центр масс этого тела, или же физическим маятником называется твёрдое тело, закреплённое на неподвижной горизонтальной оси (оси подвеса), не проходящей через центр тяжести, и совершающее колебания относительно этой оси под действием силы тяжести. В отличие от случая математического маятника, массу такого тела нельзя считать точечной.

22.

Колебания бывают двух типов: свободные и вынужденные. Свободные колебания возникают за счет внутренних сил системы, после того как она была выведена из состояния равновесия. Вынужденные колебания возникают за счет внешней периодической силы.

Самым простым колебательным движением тела является гармоническое колебание. Гармоническим называют колебание, в процессе которого величины, характеризующие движение (смещение, скорость, ускорение и др.), изменяются по закону синуса или косинуса (гармоническому закону). В общем виде этот закон задается формулой:

x(t)=Asin(ωt+φ0),

где x(t) — значение изменяющейся величины в момент времени t, A — амплитуда колебаний, ω — циклическая (круговая) частота колебаний, φ0 — начальная фаза колебаний.

Гармонические колебания являются периодическими. Период T этих колебаний равен периоду функции sin(ωt+φ0), то есть

T=2πω.

Очень часто как свободные, так и вынужденные колебания в различных механических колебательных системах имеют форму гармонических колебаний. Поведение тела, совершающего колебания по гармоническому закону, описывается дифференциальным уравнением вида

x″+ω2x=0,

где x″ — вторая производная координаты x тела по времени t , то есть проекция ax его ускорения на ось x.

23.

Статика - раздел механики, изучающий равновесие твёрдых тел.

Твердое тело – тело, расстояние между любыми двумя точками которого сохраняется с течением времени.

Сформулируем условия равновесия тела. Если тело находится в равновесии, то одновременно выполняются два условия.

Первое условие равновесия тела заключается в том, что векторная сумма всех сил, действующих на тело, равна нулевому вектору:

F1→+F2→+F3→+…=0→.

Второе условие равновесия тела заключается в том, что алгебраическая сумма всех моментов сил, действующих на тело, равна нулю:

±M1±M2±M3+…=0,

где момент силы пишется со знаком «»«+», если сила стремится повернуть тело по часовой стрелке, и со знаком «»«–», если сила стремится повернуть тело против часовой стрелки.

Обратим внимание на то, что во втором условии равновесия ничего не сказано про полюс. Дело в том, что если векторная сумма всех сил равна нулевому вектору, то алгебраическая сумма всех моментов сил, действующих на тело, не зависит от выбора полюса, поэтому во втором условии равновесия полюс можно брать в любой точке.

Два условия равновесия являются необходимыми, но не являются достаточными. Приведем пример. Рассмотрим равномерно катящееся без проскальзывания колесо по горизонтальной поверхности. Оба условия равновесия выполняются, однако тело движется.

Большинство задач по статике сводятся к записи двух условий равновесия.

Виды равновесий тела: безразличное, устойчивое, неустойчивое. Катящееся по горизонтальной поверхности колесо – пример безразличного равновесия. Если колесо остановить в любой точке, оно окажется в равновесном состоянии. Наряду с безразличным равновесием в механике различают устойчивые и неустойчивые состояния равновесия. Состояние равновесия называется устойчивым, если при малых отклонениях тела от этого состояния возникают силы или моменты сил, стремящиеся возвратить тело в равновесное состояние. При малом отклонении тела из состояния неустойчивого равновесия возникают силы или моменты сил, стремящиеся удалить тело от положения равновесия. Шар, лежащий на плоской горизонтальной поверхности, находится в безразличном состоянии равновесия. Шар, находящийся в верхней точке сферического выступа, – пример неустойчивого равновесия. Наконец, шар на дне сферического углубления находится в состоянии устойчивого равновесия.

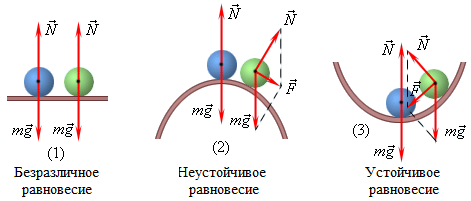
В положении устойчивого равновесия тело обладает минимальной потенциальной энергией. При выведении тела из этого положения его потенциальная энергия увеличивается. Если работу над телом совершает только сила тяжести, то в положении устойчивого равновесия центр тяжести тела находится на наименьшей высоте.

24.

Величиной, характеризующей взаимодействие частей жидкости или газа друг с другом и со стенками сосуда, является давление.

ДАВЛЕНИЕ

Величина, равная отношению модуля силы давления F, действующей по нормали (перпендикулярно) к плоской поверхности, к площади S этой поверхности:

p=FS.

В системе СИ давление измеряется в НмН/м2. Эта единица давления носит название Паскаль (Па). Итак, Па[p]=Па.

Уточним, что следует понимать под давлением в жидкости или газе.

Поместим в жидкость или газ небольшую плоскую пластину. Одну из сторон этой пластины назовем площадкой. Жидкость (газ) давит на площадку с некоторой силой F. Если площадь площадки S, то давление жидкости на площадку p=FS. Из условия равновесия вырезанной мысленно из жидкости (газа) призмы с основанием в виде прямоугольного треугольника, находящейся в месте расположения площадки, можно вывести, что давление на площадку в жидкости или газе не зависит от ориентации площадки. Вывод приводить не будем. Теперь можно дать определение давления в жидкости или газе.

ДАВЛЕНИЕ В НЕКОТОРОЙ ТОЧКЕ ЖИДКОСТИ (ГАЗА)

Давление жидкости (газа) на небольшую площадку, произвольно ориентированную и помещенную вблизи этой точки.

ОПРЕДЕЛЕНИЕ

Плотностьρ − величина, показывающая, какова масса данного вещества m, взятого в единице объема V:

ρ=mV.

В системе СИ плотность измеряется кгм[ρ]=кг/м3.

Плотность − табличная величина. Она экспериментально измерена для многих веществ. Но в отдельных «нестандартных» ситуациях приходится проводить эксперименты по измерению плотности.

· Для твердых тел плотность можно определить, измерив объем и массу или проведя гидростатическое взвешивание, сравнивая вес тела в воздухе и в известной жидкости.

· Плотности жидкостей можно определять, сравнивая их с другими жидкостями, например с помощью U-образной трубки по разности уровней. По силе Архимеда с помощью ареометра.

Рассмотрим связь между давлениями в различных точках жидкости. Будем рассматривать покоящуюся жидкость в неподвижном сосуде. Дополнительное давление в жидкости, возникающее из-за силы тяжести, учитывать не будем. Пусть жидкость заключена в замкнутый сосуд произвольной формы.

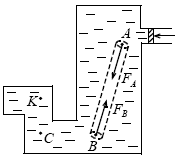
Будем давить на поршень. Покажем, что давление pA в точке A равно давлению pB в точке B. Для этого выделим мысленно внутри жидкости тонкий цилиндр, ось которого проходит через точки A и B, а основания площадью S каждое перпендикулярны оси. На части боковой поверхности цилиндра из жидкости со стороны окружающей жидкости действуют силы давления, перпендикулярные оси цилиндра. На основания цилиндра жидкость действует с силами FA=pAS и FB=pBS, направленными вдоль оси AB. Поскольку цилиндр находится в покое, то FA=FB, т. е. pAS=pBS. Отсюда pA=pB. Значит, давление в точках A и B одно и то же. Аналогично доказывается равенство давлений в точках B и C и в точках C и K. Таким образом, приходим к выводу, что давление во всех точках внутри жидкости одинаково. Поршень давит на жидкость на ее границе в одном месте, но это давление ощущается во всей жидкости. Мы получили закон Паскаля: давление, оказываемое на жидкость в каком-либо одном месте на ее границе, передается без изменения во все точки жидкости.

Этот закон был установлен экспериментально французским физиком и математиком Блэзом Паскалем (1623–1662) и носит его имя. Это же справедливо и для газов. Справедлив для газов и закон Паскаля.

Отметим, что закон Паскаля выведен и сформулирован здесь при условии отсутствия силы тяжести. Наличие силы тяжести не изменяет сути закона и вносит дополнительную связь между давлениями в различных точках жидкости или газа.

25.

На поверхности твердого тела, погруженного в жидкость (газ), действуют силы давления. Эти силы увеличиваются с глубиной погружения, и на нижнюю часть тела будет действовать со стороны жидкости большая сила, чем на верхнюю.

Равнодействующая всех сил давления, действующих на поверхность тела со стороны жидкости, называется выталкивающей силой. Другое название этой силы – сила Архимеда. Истинная причина появления выталкивающей силы – это наличие различного гидростатического давления в разных точках жидкости.

ЗАКОН АРХИМЕДА

Выталкивающая сила, действующая на тело, погруженное в жидкость, равна по модулю весу вытесненной жидкости и противоположно ему направлена.

Закон открыт величайшим механиком и математиком Древней Греции Архимедом (287–212 гг. до н. э.).

Приведенная формулировка закона Архимеда справедлива, если вся поверхность тела соприкасается с жидкостью или если тело плавает в жидкости, или если тело частично погружено в жидкость через свободную (не соприкасающуюся со стенками) поверхность жидкости.

Если же часть поверхности тела плотно прилегает к стенке или дну сосуда так, что между ними нет прослойки жидкости, то закон Архимеда неприменим!

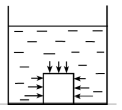
Иллюстрацией к сказанному служит опыт, когда ровную нижнюю поверхность деревянного кубика натирают парафином и плотно приставляют ко дну сосуда. Затем осторожно наливают воду. Кубик не всплывает, т. к. со стороны воды на него действует сила, прижимающая его ко дну, а не выталкивающая вверх. Известно, что это представляет опасность для подводной лодки, легшей на грунт.

Закон Архимеда применим и в случае погружения тела в газ.

Строго говоря, в законе Архимеда вес вытесненной жидкости надо брать в вакууме, а не в воздухе, так как вес жидкости в воздухе меньше веса этой жидкости в вакууме на величину веса воздуха, вытесненного этой жидкостью. Но это различие обычно мало, и им пренебрегают.

Если тело погружено в жидкость частично, то результирующая выталкивающая сила со стороны жидкости и воздуха равна сумме веса вытесненной жидкости и вытесненного этим телом воздуха. Здесь оба веса берутся в вакууме.

Лодка из железа, спущенная на воду, плывет, а эта же лодка, полностью погруженная в воду (затопленная), тонет. Из этого примера видно, что одно и то же тело может плавать, а может и тонуть. Все зависит от того, как тело приведено в контакт с жидкостью. Поэтому имеет смысл рассмотреть два случая взаимодействия тела с жидкостью.

Й СЛУЧАЙ

Тело плавает в жидкости, т. е. находится в покое, частично погрузившись в жидкость. Это может быть любое тело, например кусок дерева или катер. Важен сам факт плавания. При этом тело соприкасается только с жидкостью и воздухом, плавая предоставленным самому себе, свободно. На начальном этапе рассмотрения вопроса о плавании не будем учитывать вес вытесненного воздуха. На тело действует направленная вниз сила тяжести ТFТ и направленная вверх сила Архимеда АFА. Поскольку сила тяжести ТFТ равна весу тела (в вакууме), а сила Архимеда АFА – весу (в вакууме) вытесненной жидкости, то можно сказать, что вес тела равен весу вытесненной жидкости. При более строгом рассмотрении вопроса с учетом веса вытесненного воздуха можно показать, что вес тела в воздухе равен весу (тоже в воздухе) вытесненной жидкости.

Итак, если тело плавает в жидкости, то вес тела в воздухе равен весу в воздухе вытесненной им жидкости.

При решении задач, когда ситуация реальна, различием в весе в воздухе и вакууме обычно пренебрегают, приравнивая вес любого тела силе тяжести, действующей на тело.

Й СЛУЧАЙ

Тело полностью погружено в жидкость и отпущено. Возьмем в руки какое-нибудь тело (кусочек дерева, стальной болт), погрузим его полностью в жидкость (например, воду) и будем удерживать неподвижно. На тело со стороны Земли действует вниз сила тяжести ТFТ=ρVg, а со стороны жидкости – вверх выталкивающая сила по закону Архимеда АЖFА=ρЖVg. Здесь V – объем тела, ρ и ЖρЖ – плотности тела и жидкости. Отпустим тело. Если окажется, что ТАFТ>FА, то тело начнет двигаться вниз, т. е. тонуть. Если будет ТАFТ<FА, то тело станет двигаться вверх, т. е. всплывать. После всплытия, когда тело будет плавать, объем погруженной в жидкость части тела окажется таким, что будет обеспечено равенство силы Архимеда (уже меньшей, чем величина АFА) и силы тяжести ТFТ. Итак, тело будет плавать, если ЖρVg<ρЖVg, т. е. Жρ<ρЖ.

Мы получили условие плавания тела: тело, предварительно полностью погруженное в жидкость, плавает в жидкости, если плотность тела меньше плотности жидкости.

Если плотности тела и жидкости равны, то полностью погруженное в жидкость тело может находиться в равновесии (покое) в любом месте жидкости, т. е. тело плавает внутри жидкости. Реально такая ситуация трудно осуществима, так как добиться строгого равенства плотностей нелегко.

Условие плавания сформулировано для тела, предварительно полностью погруженного в жидкость. Предварительное полное погружение важно, так как, например, металлическая миска, не полностью погруженная в воду, может плавать, а полностью

погруженная утонет.

Условие плавания сформулировано для однородного тела, т. е. тела, плотность которого одинакова во всех точках тела. Это условие плавания справедливо и для неоднородного тела, например, куска льда с полостью внутри или стеклянной бутылки, заполненной частично водой и закрытой пробкой. В таком случае под плотностью тела надо понимать его среднюю плотность, т. е. отношение массы тела к его объему.

26.

Земля окружена воздушной оболочкой, состоящей из смеси газов. Эта оболочка называется атмосферой. Каждый горизонтальный слой атмосферы сжат весом верхних слоев. Поэтому давление в нижних слоях атмосферы больше, чем в верхних. При этом и плотность воздуха в нижних слоях значительно больше, чем в верхних. Это связано с тем, что газы под воздействием давления могут сильно уменьшить свой объем. Жидкости же обладают очень малой сжимаемостью и практически не изменяют плотность даже при больших давлениях. Атмосферное давление на уровне моря равно примерно Па105 Па, то есть Па100000 Па. Это желательно помнить. С увеличением высоты над уровнем моря атмосферное давление уменьшается. На высоте примерно км5,5 км оно уменьшается вдвое.

Значение атмосферного давления впервые экспериментально определил в 1634 году итальянский ученый Эванджелиста Торричелли, создав простейший ртутный барометр. Опыт Торричелли состоит в следующем. Стеклянную трубку длиной около метра, запаянную с одного конца, полностью заполняют ртутью. Затем закрывают отверстие трубки, переворачивают ее и погружают открытым концом в чашу с ртутью.

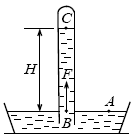
Часть ртути из трубки выливается, и в ней остается столб ртути высотой H. Давление в трубке над ртутью равно нулю (если пренебречь ничтожным давлением паров ртути), так как там пустота (вакуум): pC=0. Давление pB в точке B равно давлению pA в точке A, поскольку в сообщающихся сосудах − чаше и трубке − точки A и B находятся на одном уровне. Давление pA равно атмосферному давлению p0. Поэтому pB=p0. Разность давлений pB−pC=ρgH, где ρ − плотность ртути. Так как pB=p0 и pC=0, то p0=ρgH. Измерив H и зная ρ, можно определить атмосферное давление в условиях опыта. Торричелли нашел, что для уровня моря ммH=760 мм.

В опыте Торричелли каждому значению H соответствует определенное значение p0. Следовательно, атмосферное давление можно измерять в миллиметрах ртутного столба. Эта единица давления получила специальное название «ТоррТорр»: Торр мм рт. ст.1 Торр=1 мм рт. ст. При этом высота столба ртути берется той, которую он имел бы при 00C. Атмосферное давление Торр760 Торр называется нормальным атмосферным давлением. Значение этого давления называется нормальной (физической) атмосферой и обозначается атм1 атм. Зная плотность ртути кгмρ=13595 кг/м3, находим по формуле p0=ρgH:

атм Торр Па.

Воздухопла́вание (аэрона́втика — от греч. аэр — воздух и наута (греч. ναυτα — плавающий, мореплаватель)) — вертикальное и горизонтальное перемещение в атмосфере Земли на летательных аппаратах легче воздуха (в отличие от авиации, использующей летательные аппараты тяжелее воздуха)^[2].

До начала 1920-х годов термин «воздухоплавание» использовался для обозначения передвижения по воздуху вообще.^[2]

Воздухоплаватель (аэронавт, аэростьер^[3]) — человек, который летает на аэростатах, занимается воздухоплаванием, поднимается в небона воздушных шарах.

27.

Движение жидкостей или газов представляет собой сложное явление. Для его описания используются различные упрощающие предположения (модели). В простейшей модели жидкость (или даже газ) предполагается несжимаемой и идеальной (т. е. без внутреннего трения между движущимися слоями). При движении идеальной жидкости не происходит превращения механической энергии во внутреннюю, поэтому выполняется закон сохранения механической энергии. Следствием этого закона для стационарного потока идеальной и несжимаемой жидкости является уравнение Бернулли, сформулированное в 1738 году. Стационарным принято называть такой поток жидкости, в котором не образуются вихри. В стационарном потоке частицы жидкости перемещаются по неизменным во времени траекториям, которые называются линиями тока. Опыт показывает, что стационарные потоки возникают только при достаточно малых скоростях движения жидкости.

Рассмотрим стационарное движение идеальной несжимаемой жидкости по трубе переменного сечения. Различные части трубы могут находиться на разных высотах.

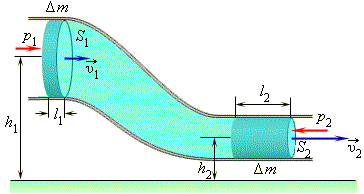
При течении идеальной несжимаемоей жидкости по трубе переменного сечения выполняется уравнение неразрывности струи:

V1⋅S1=V2⋅S2.

Таким образом, при переходе жидкости с участка трубы с большим сечением на участок с меньшим сечением скорость течения возрастает, т. е. жидкость движется с ускорением. Следовательно, на жидкость действует сила. В горизонтальной трубе эта сила может возникнуть только из-за разности давлений в широком и узком участках трубы. Давление в широком участке трубы должно быть больше, чем в узком участке. Если участки трубы расположены на разной высоте, то ускорение жидкости вызывается совместным действием силы тяжести и силы давления. Сила давления – это упругая сила сжатия жидкости. Несжимаемость жидкости означает лишь то, что появление упругих сил происходит при пренебрежимо малом изменении объема любой части жидкости.

Так как жидкость предполагается идеальной, то она течет по трубе без трения. Поэтому к ее течению можно применить закон сохранения механической энергии:

p1+ρgh1+ρV122=p2+ρgh2+ρV222.

Это и есть уравнение Бернулли. Из него следует, что сумма

p+ρgh+ρV22=const

остается неизменной вдоль всей трубы. В частности, для горизонтально расположенной трубы (h1=h2) уравнение Бернулли принимает вид:

p+ρV22=const.

Величина p − статическое давление в жидкости. Оно может быть измерено с помощью манометра, перемещающегося вместе с жидкостью. Практически давление в разных сечениях трубы измеряется с помощью манометрических трубок, вставленных через боковые стенки в поток жидкости, так чтобы нижние концы трубок были параллельны скоростям частиц жидкости. Из уравнения Бернулли следует:

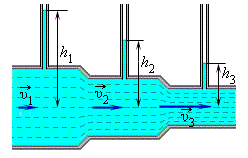
Давление в жидкости, текущей по горизонтальной трубе переменного сечения, больше в тех сечениях потока, в которых скорость ее движения меньше, и наоборот, давление меньше в тех сечениях, в которых скорость больше.

Если сечение потока жидкости достаточно велико, то уравнение Бернулли следует применять к линиям тока, т. е. линиям, вдоль которых перемещаются частицы жидкости при стационарном течении. Например, при истечении идеальной несжимаемой жидкости из отверстия в боковой стенке или дне широкого сосуда линии тока начинаются вблизи свободной поверхности жидкости и проходят через отверстие.

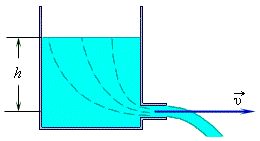
Поскольку скорость жидкости вблизи поверхности в широком сосуде пренебрежимо мала, то уравнение Бернулли принимает вид:

p0+ρgh=p0+ρV22,

где p0 − атмосферное давление, h − перепад высоты вдоль линии тока. Таким образом,

V=2gh.

Это выражение для скорости истечения называют формулой Торричелли. Скорость истечения идеальной жидкости из отверстия в сосуде такая же, как и при свободном падении тела с высоты h без начальной скорости.

В отличие от жидкостей, газы могут сильно изменять свой объем. Расчеты показывают, что сжимаемостью газов можно пренебречь, если наибольшие скорости в потоке малы по сравнению со скоростью звука в этом газе. Таким образом, уравнение Бернулли можно применять к достаточно широкому классу задач аэродинамики.

28.

Решение каждой из задач следует выполнять по следующему алгоритму:

· Дано (что и через какие величины нужно искать; перечисляем все вопросы задачи, чтобы не забыть).

· Рисунки (чтобы самому наглядно представить ситуацию, пояснить свое решение, обозначить введенные величины, провести геометрическое решение).

· Общий вид (универсальное решение для любых значений параметров; возможность анализа полученных функций [графики, максимумы, минимумы, характер поведения в зависимости от отдельных параметров], сокращение неизвестных величин, введенных по ходу решения задачи).

· Графики (наглядно, информативно, применение геометрических методов вместо алгебраических).

· Система СИ.

· Выделение независимых исходных уравнений, комментарии к ним.

· Ответ.

· Проверка размерности и на предельные случаи.

В физике нехорошо делать переобозначения типа: пусть скорость V равна x (это пережиток из математики).

Следует избегать ранней подстановки численных значений известных величин, прежде чем из уравнения выражена искомая величина.

1.Все вещества – жидкие, твердые и газообразные – образованы из мельчайших частиц – молекул, которые сами состоят из атомов («элементарных молекул») . ... 2.Атомы и молекулы находятся в непрерывном хаотическом движении.

3.Частицы взаимодействуют друг с другом силами, имеющими электрическую природу.

29.

Идеальный газ – это модель разреженного газа, в которой пренебрегается взаимодействием между молекулами. Силы взаимодействия между молекулами довольно сложны. На очень малых расстояниях, когда молекулы вплотную подлетают друг к другу, между ними действуют большие по величине силы отталкивания.

Идеальный газ — математическая модель газа, в которой в рамках молекулярно-кинетической теории предполагается, что:

1. потенциальной энергией взаимодействия частиц, составляющих газ, можно пренебречь по сравнению с их кинетической энергией;

2. суммарный объём частиц газа пренебрежимо мал;

3. между частицами нет дальнодействующих сил притяжения или отталкивания, соударения частиц между собой и со стенками сосуда абсолютно упруги;

4. время взаимодействия между частицами пренебрежимо мало по сравнению со средним временем между столкновениями.

В расширенной модели идеального газа, частицы, из которых он состоит, имеют форму упругих сфер или эллипсоидов, что позволяет учитывать энергию не только поступательного, но и вращательно-колебательного движения, а также не только центральные, но и нецентральные столкновения частиц^[1]. В рамках термодинамикиидеальными называются гипотетические (реально не существующие) газы, подчиняющиеся термическому уравнению состояния Клапейрона — Менделеева^[2][3][4].

Модель широко применяется для решения задач термодинамики газов и аэрогазодинамики. Например, воздух при атмосферном давлении и комнатной температуре с большой точностью описывается данной моделью. В случае экстремальных температур или давлений требуется применение более точных уравнений состояния реальных газов, например уравнения Ван-дер-Ваальса, в котором учитывается притяжение между молекулами .

Различают классический идеальный газ (его свойства выводятся из законов классической механики и описываются статистикой Больцмана) и квантовый идеальный газ (свойства определяются законами квантовой механики, описываются статистиками Ферми — Дирака или Бозе — Эйнштейна)

30.

Штерна опыт

экспериментальное определение скоростей теплового движения молекул газа, осуществленное О. Штерном в 1920. Ш. о. подтвердил правильность основ кинетической теории газов (См. Кинетическая теориягазов). Исследуемым газом в опыте служили разреженные пары серебра, которые получались при испарениислоя серебра, нанесённого на платиновую проволоку, нагревавшуюся электрическим током. Проволокарасполагалась в сосуде, из которого воздух был откачан, поэтому атомы серебра беспрепятственноразлетались во все стороны от проволоки. Для получения узкого пучка летящих атомов на их пути былаустановлена преграда со щелью, через которую атомы попадали на латунную пластинку, имевшую комнатнуютемпературу.Атомы серебра осаждались на ней в виде узкой полоски, образуя серебряное изображение щели. Специальным устройством весь прибор приводился в быстрое вращение вокруг оси, параллельной плоскостипластинки. Вследствие вращения прибора атомы попадали в др. место пластинки: пока они пролеталирасстояние l от щели до пластинки, пластинка смещалась. Смещение растет с угловой скоростью ω прибора иуменьшается с ростом скорости v атомов серебра. Зная ω и l, можно определить v. Т. к. атомы движутся сразличными скоростями, полоска при вращении прибора размывается, становится шире. Плотность осадка вданном месте полоски пропорциональна числу атомов, движущихся с определённой скоростью. Наибольшаяплотность соответствует наиболее вероятной скорости атомов. Полученные в Ш. о. значения наиболеевероятной скорости хорошо согласуются с теоретическим значением, полученным на основе Максвеллараспределения (См. Максвелла распределение) молекул по скоростям.

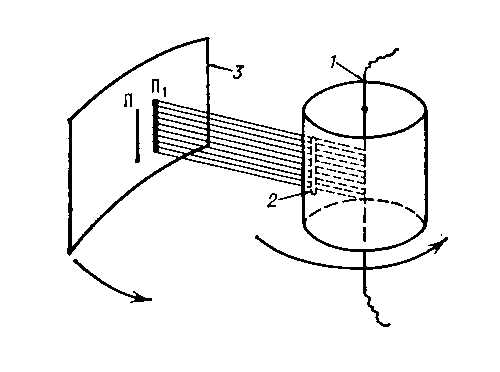
Схема опыта Штерна: 1 — платиновая проволока с нанесённым на неё слоем серебра; 2 — щель, формирующая пучок атомов серебра; 3 — пластинка, на которой осаждаются атомы серебра; П и П₁ — положения полосок осажденного серебра при неподвижном приборе и при вращении прибора.

31.