Разрешенные и запрещенные переходы

Из выражения 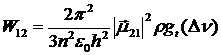следует, что W=0, если |μ₂₁|=0. Это имеет место, когда обе собственные функции U₁ и U₂ являются одновременно симметричными или антисимметричными (f(-r)=f(r) или f(-r)=-f(r)). В этом случае вклады в 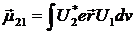в точках r, -r равны, но имеют противоположные знаки. Следовательно, необходимо знать в каких случаях волновые функции U(r) будут симметричны или антисимметричны. Это имеет место, когда гамильтониан системы 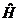не меняется при замене r на –r, т.е. когда

. (*)

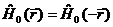В этом случае для любой собственной функции U_n(r) справедливо равенство

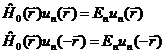
Эти равенства показывают, что u_n(r) и u_n(-r) являются собственными функциями оператора 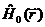с одним и тем же собственным значением E_n

Из квантовой механики известно, что для невырожденных уровней (не считая произвольного выбора знака) каждому собственному значению соответствует одна собственная функция, т.е. u_n(-r)=±u_n(r). Следовательно, если гамильтониан 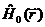является симметричным, то его собственные функции должны быть либо симметричными, либо антисимметричными. Т.е. функции имеют определенную четность.

Гамильтониан инвариантен относительно операции инверсии, очевидно, в двух случаях: если система имеет центр инверсии, и, во-вторых, для изолированного атома. Для изолированного атома энергия взаимодействия равна потенциальной энергии взаимодействия с ядром (описывается симметричной функцией) и взаимодействия с другими электронами (энергия зависит от |r_i-r_k| т.е. от расстояния между электронами).

Равенство (*) не выполняется, например, когда атом находится во внешнем электрическом поле, не обладающем центром инверсии. В этом случае волновые функции не имеют определенной четности.

Электродипольные переходы происходят только между состояниями с противоположной четностью и состояния имеют определенную четность в том случае, когда гамильтониан системы инвариантен относительно инверсии.

Если W=0, то переход называют запрещенным в электродипольном приближении. Но реально вероятность перехода между уровнями может отличаться от нуля из-за магнитодипольных переходов или из-за слабого примешивания других состояний.

Магнитодипольные переходы разрешены между состояниями с одинаковой четностью.

Уширение спектральных линий

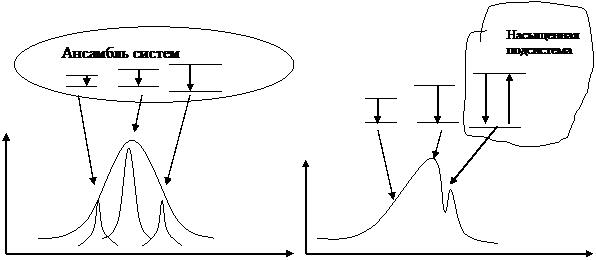
Когда линия каждого отдельного атома уширяется в одинаковой степени, и резонансные частоты всех атомов совпадают, линия называется однородно уширенной. Если при одинаковой ширине линий отдельных атомов, сильно различаются резонансные частоты, что приводит к уширению наблюдаемой линии, линия называется неоднородно уширенной.

Однородное уширение

Столкновительное уширение проявляется в газах при столкновении с другими атомами, ионами, стенками и т.д., а в твердых телах при столкновении с фононами решетки. После столкновения волновые функции атома и его дипольный момент 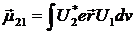будут иметь другую фазу

столкновении с фононами решетки. После столкновения волновые функции атома и его дипольный момент 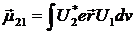будут иметь другую фазу относительно фазы падающей волны. Т.к. имеет значение только относительная фаза, то в системе координат, связанной с частицей, можно считать, что изменилась скачком фаза падающей волны. Ясно, что в системе координат атома волна больше не является монохроматической. В этом случае для плотности энергии в частотном интервале от ν' до ν'+dν' необходимо записать 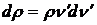. Эту элементарную плотность энергии используем в выражении для монохроматического излучения. Полная вероятность перехода получается интегрированием по всему спектру излучения, откуда находим

.

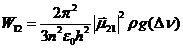Введя в рассмотрение плотность вероятности для времени между двумя последовательными столкновениями

,

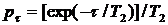где T₂ среднее время τ_c между двумя столкновениями, и

.

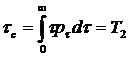Далее используется теорема Винера-Хинчина.

Функция g(Δν) имеет вид (лоренцева кривая):

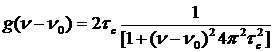
Столкновительное уширение приводит к лоренцевой форме спектральной линии. Однако в реальности длительность времени столкновения конечна (а не равно нулю как предполагалось выше) и это существенно усложняет задачу. Тем не менее, при условии, что время столкновения много меньше τ_c среднего времени между двумя столкновениями Δτ_c<<τ_c функция 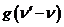достаточно точно описывается лоренцевой кривой.

Второй механизм однородного уширенияспонтанное излучение, которое неизбежно присутствует в случае любого перехода. Данное уширение называют естественным или собственным. Причем

.

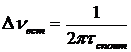Форма линии также является лоренцевой. Отметим, что для разрешенного электродипольного перехода в середине видимого диапазона τ_спонт~10 нс, и тогда Δν_ест=16 МГц.

Неоднородное уширение

Неоднородное уширение проявляется в том случае, когда имеется некий механизм, приводящий к распределению резонансных частот частиц в ансамбле в некоторой полосе частот с центром в ν₀, и что относительная плотность распределения этих частот равна .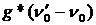

В формуле 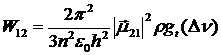g_t в случае неоднородного уширения является гауссовым распределением. В реальном случае g_t заменяется сверткой функций g для однородного уширения и неоднородного, т.е. сверткой лоренцевой и гауссовой кривых. В предельном случае, когда Δν_однор<<Δν_{неоднор} неоднородное уширение приведет к гауссовой форме спектральной кривой.

В газах к неоднородному уширению приводит доплеровское смещение частоты 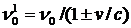. При переходе к неподвижному атому это можно интерпретировать как сдвиг уровней (или изменение резонансной частоты перехода). В твердых телах неоднородное уширение происходит из-за нарушений структуры кристаллической решетки.

Безызлучательная релаксация

Эта релаксация может осуществляться большим количеством различных способов. Аналитическое описание всевозможных механизмов релаксации практически во всех случаях потребует очень большого времени (что выльется в спецкурс), поэтому ограничимся несколькими примерами на качественном уровне.

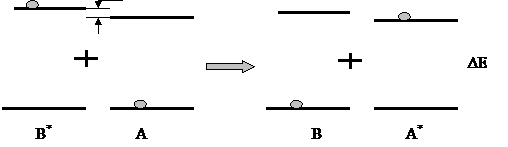
Процесс неупругого столкновения – передача энергии окружающим частицам в форме электронного и колебательного возбуждения или поступательного движения. Этот процесс особенно эффективен, если разность энергий возбужденных энергетических уровней ΔЕ ≤ kT (см. рис).

.

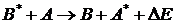В случае газового разряда может происходить также столкновение между электроном и возбужденной частицей

.

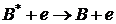Энергия возбуждения передается электрону в форме кинетической энергии. Этот процесс иногда называют сверхупругим столкновением, или столкновением второго рода. В кристаллах преобладающим столкновительным механизмом является столкновение активных ионов с фононами.

Также, например, бывает существенным диполь дипольное взаимодействие (флип-флоп переходы).

Фононы, СРР; баллистика фононов, Орбах, Раман. Процессы СРР.

При безызлучательной релаксации

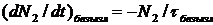
В полупроводниках безызлучательная релаксация происходит за счет электронно-дырочной рекомбинации на глубоких ловушках. При существовании всех видов релаксации время жизни на возбужденном уровне определяется суммарной скоростью всех возможных переходов. И ширина спектральной линии будет определяться общим временем жизни τ:

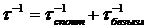
Всё это приводит к уширению спектральной линии.

Квантовый выход люминесценции определяют как отношение числа излученных фотонов к полному числу атомов, первоначально переведенных на возбужденный уровень.

Насыщение

Однородно уширенная линия

В этом разделе рассматривается поведение двухуровневой системы (с частотой перехода ν₀) в среде, облучаемой монохроматической ν≈ν₀ электромагнитной волной большой интенсивности I. Первоначально процесс поглощения 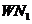будет преобладать над вынужденным излучением 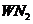т.к. N₁>N₂. При большой интенсивности I населенности будут выравниваться. Это явление называется насыщением.

Насыщение поглощения. Рассмотрим поглощающий переход, и

предположим, что линия является однородно уширенной. С учетом вынужденных и спонтанных переходов для населенностей можно записать два уравнения

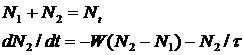
Если рассматривать разность населенностей 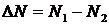, то оба уравнения приводятся к одному: во второе подставляем первое, получаем

,

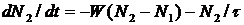а после вычитания окончательно

.

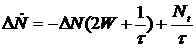В стационарном случае 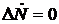, и получаем

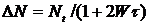
Следовательно, разность населенностей между двумя уровнями зависит от времени релаксации (от характеристик вещества) и интенсивности падающего излучения. С увеличением I вероятность вынужденных переходов W также увеличивается. Это приводит к уменьшению разности населенностей ΔN. Когда Wτ>>1, ΔN≈0, 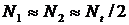. Для поддержания заданной разности населенностей средой должна поглощаться определенная мощность.

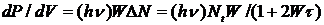
В случае насыщения (Wτ>>1)

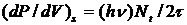
Всем известно понятие сечение перехода. В случае однородной плоской волны вероятность перехода пропорциональна интенсивности волны, поэтому сечение перехода можно определить так:

,

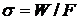где 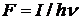- плотность потока фотонов падающей волны. Тогда W можно выразить следующим образом:

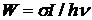
С учетом замечаний, набранных курсивом, выражения

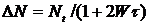
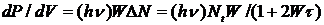
можно переписать в виде

,

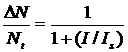
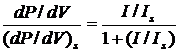где 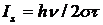представляет параметр, характеризующий среду. Эта величина называется интенсивностью насыщения. При I=I_s получаем .

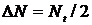Следует отметить, что при насыщении однородно уширенной линии её форма не изменяется, а изменяется только интенсивность.

Насыщение усиления. Рассмотрим четырехуровневую систему. Пусть переход 2→1 усиливает излучение. Инверсия создается накачкой W_pN_g. Далее полагаем, что переходы 3→2, 1→g осуществляются с очень большой скоростью, так что N₃≈N₁≈0. При этих предположениях запишем скоростное уравнение для населенности 2 уровня

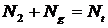
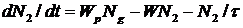
или

.

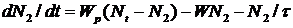В равновесном состоянии (когда 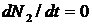) из вышеприведенного уравнения находим

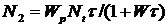при условии .

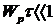Последнее условие, как уверяет Звелто, как правило, выполняется в лазерных материалах. С помощью 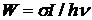выражение для N₂ можно переписать в виде

,

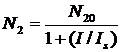где 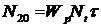- населенность второго уровня в отсутствие насыщающего пучка (при I=0), а 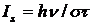. I_s – интенсивность насыщения. Отметим, что при тех же самых значениях величин 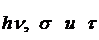интенсивность насыщения в четырехуровневой схеме в 2 раза больше, чем в двухуровневой.