Т.С. Рогожина, Л.Ю. Фроленкова

Т.С. Рогожина, Л.Ю. Фроленкова

Задания

для выполнения типового расчета по разделу электричество и магнетизм курса общей физики с примерами решения задач

Дисциплина "Общая физика"

Специальности: 151001 (120100) - "Технология машиностроения";

151002 (120200) - "Металлообрабатывающие станки и комплексы";

151003 (121300) - "Инструментальные системы машиностроительных производств"

Печатается по решению

Редакционно-издательского совета ОрелГТУ

Орел 2005

УДК 537.6/.8(075)

ББК 22.33я7

Р59

Рецензенты:

Кафедра "Физика" Орловского государственного технического университета

Кандидат физико-математических наук, доцент В.Н. Преснецов,

Кафедра "Теоретическая физика" Орловского государственного университета кандидат физико-математических наук, доцент О.И. Марков.

Р59 Рогожина Т.С. Задания для выполнения типового расчета по разделу электричество и магнетизм курса общей физики с примерами решения задач: Учебно-методическое пособие / Т.С. Рогожина, Л.Ю. Фроленкова. – Орел: ОрелГТУ, 2005. – 57 с.

Настоящее учебно-методическое пособие предназначено для студентов обучающихся по инженерно-технических специальностям и изучающим дисциплину «Физика». Оно содержит краткие теоретические сведения, необходимые для выполнения типового расчета, примеры решенных задач, а также требования по подготовке, выполнению и оформлению типового расчета.

Учебно-методическое пособие соответствует требованиям государственных образовательных стандартов высшего профессионального образования по специальностям технического профиля обучения ОрелГТУ, а также рабочим программам по дисциплине "Физика".

УДК 537.6/.8(075)

ББК 22.33я7

Р59

ã ОрелГТУ, 2005

ã Рогожина Т.С.,

Фроленкова Л.Ю., 2005

СОДЕРЖАНИЕ

Введение. 5

1. Общие методические указания по решению и оформлению типового расчета (ТР) 6

1.1 Методические указания по решению задач. 6

1.2 Общие указания по оформлению типового расчета. 8

2. Тема: Напряженность электрического поля. 10

2.1 Основные формулы и указания к решению задачи. 10

2.2 Пример решения задачи. 12

2.3 Задание для самостоятельного выполнения по вариантам. 15

3. Тема: Основные законы постоянного тока. 19

3.1 Основные формулы и указания к решению задачи. 19

3.2 Пример решения задачи. 20

3.3 Задание для самостоятельного выполнения по вариантам. 23

4. Тема: Магнитное поле постоянного тока. 26

4.1 Основные формулы и указания к решению задачи. 26

4.2 Пример решения задачи. 27

4.3 Задание для самостоятельного выполнения по вариантам. 29

5. Тема: Сила, действующая на заряд, движущийся в магнитном поле. 31

5.1 Основные формулы и указания к решению задачи. 31

5.2 Пример решения задачи. 31

5.3 Задание для самостоятельного выполнения по вариантам. 33

6. Тема: Электромагнитная индукция. 37

6.1 Основные формулы и указания к решению задачи. 37

6.2 Пример решения задачи. 38

6.3 Задание для самостоятельного выполнения по вариантам. 40

7. Тема: Переменный ток. 42

7.1 Основные формулы и указания к решению задачи. 42

7.2 Примеры решения задач. 44

7.3 Задание для самостоятельного выполнения по вариантам. 48

Литература. 51

Приложение 1. 52

Основные физические постоянные. 52

Приложение 2. 53

Диэлектрическая проницаемость среды e. 53

Приложение 3. 54

Удельное сопротивление r (при 20 °С) 54

Приложение 4. 55

температурный коэффициент a (при 20 °С) 55

Приложение 5. 56

Приставки для образования десятичных кратных и дольных единиц. 56

Приложение 6. 57

Образец оформления титульного листа работы.. 57

Введение

Решение задач по физике – это хороший способ применения теоретических знаний на практике. Причем, с одной стороны, сам процесс решения помогает более глубоко и сознательно овладеть изучаемым материалом, с другой – знание теоретического материала есть непременное условие умения решать задачи.

В данном учебно-методическом пособии представлены задания для выполнения типового расчета по разделу общей физики "Электричество и магнетизм", которые охватывают основное содержание указанного раздела. При составлении пособия авторы ставили своей задачей не только проконтролировать качество усвоенного студентами материала, но и дать возможность студенту, проработав и разобрав примеры решения задач, закрепить свои знания при выполнении самостоятельного задания. Поэтому каждому заданию предшествует подробный разбор примера задачи по указанной теме, что позволит студентам выполнить все задания самостоятельно.

Пособие имеет приложения с физическими постоянными, которые могут понадобиться при решении задач (приложения 1 – 5).

Задания могут также использоваться для контрольных работ, при проведении практических занятий по различным темам раздела "Электричество и электромагнетизм", а также для самоподготовки студентов к экзамену по общей физике.

Подбор материала соответствует действующей программе курса общей физики. Пособие рассчитано на студентов инженерно-технических специальностей.

1. Общие МЕТОДИЧЕСКИЕ УКАЗАНИЯ ПО РЕШЕНИЮ и оформлению ТИПОвого расчета (тр)

Пример решения задачи

Две концентрические проводящие сферы радиусами R₁ = 6 см и R₂ = 10 см несут соответственно заряды Q₁ = 1 нКл и Q₂ = –0,5 нКл. Найти напряженность Е поля в точках, отстоящих от центра на расстояниях r₁ = 5 см, r₂ = 9 см, r₁ = 15 см. Построить график Е(r).

Решение. Заметим, что точки, в которых требуется найти напряженности электрического поля, лежат в трех областях (рис. 2.1): области , области , области .

1. Для определения напряженности в области I проведем гауссову поверхность радиусом r₁ и воспользуемся теоремой Остроградского–Гаусса: (т.к. суммарный заряд, находящийся внутри гауссовой поверхности равен нулю). Из соображений симметрии Следовательно, и (напряженность поля в области I) во всех точках, удовлетворяющих условию , будет равна нулю, т.е. Е₁ = 0.

Рис. 2.1. Построение гауссовых поверхностей для расчета

напряженностей электрического поля.

2. В области II гауссову поверхность проведем радиусом r₂. В этом случае (диэлектрическую проницаемость среды будем считать равной единице (вакуум)):

(2.18)

(т.к. внутри гауссовой поверхности находится только заряд ). Из соображения симметрии то Е можно вынести за знак интеграла:

, или (2.19)

Обозначив напряженность Е для области II через , получим

(2.20)

где – площадь гауссовой поверхности. Тогда

. (2.21)

3. В области III гауссова поверхность проводится радиусом r₃. Обозначим напряженность Е области III через Е₃ и учтем, что в этом случае гауссова поверхность охватывает обе сферы и, следовательно, суммарный заряд будет равен . Тогда

. (2.22)

Заметив, что это выражение можно переписать в виде:

. (2.23)

Убедимся в том, что правая часть равенств (2.21) и (2.23) дает единицу напряженности:

. (2.24)

Выразим все величины в единицах СИ (Q₁ = 10^‑9 Кл, Q₂ = –0,5×10^‑9 Кл, r₁ = 0,09 м, r₂ = 0,15 м, м/Ф) и произведем вычисления:

Е₂ = 1,11 кВ/м; Е₃ = 200 кВ/м.

Построим график E(r). В области Е = 0. В области изменяется по закону В точке напряженность В точке (r стремится к слева) . В области изменяется по закону , причем в точке (r стремится к справа) . Таким образом, функция E(r) в точках и терпит разрыв.

График зависимости E(r) представлен на рис. 2.2.

Рис. 2.2. График зависимости E(r)

2.3 Задание для самостоятельного выполнения по вариантам

Дано n проводящих фигур (сфер, цилиндров, плоскостей) или шар из изотропного диэлектрика. Каждая фигура несет заряд, характеризующийся объемной r_n, поверхностной s_n или линейной t_n плотностью заряда. Точки А, В, С находятся на расстояниях r_А, r_В, r_С от центра или оси симметрии фигуры. Взаимодействие осуществляется в вакууме. Данные для решение задач приведены в табл. 2.1 и на рис. 2.3.

Фигуре с номером 1 соответствуют размеры R₁ и величины s₁, r₁, t₁ и т.д. (рис. 2.3). Если в строке табл. 2.1 с номером вашего варианта какие-то клетки не заполнены, значит для решения вашей задачи эти данные не нужны.

1. Используя теорему Остроградского-Гаусса и принцип суперпозиции электростатических полей, найти зависимость напряженности электрического поля от расстояния Е(r) для всех областей (внутри фигуры, между фигурами и вне фигур).

2. Сделать схематический рисунок и показать направление вектора Е в каждой области.

3. Вычислить напряженность Е в точках А, В, С удаленных от центра симметрии фигур на расстояния r_i.

4. Построить график зависимости Е(r) для всех областей.

Данные для выполнения задания. Таблица 2.1

№ вари-анта	Число и форма фигур	Размеры фигур, м	Поверхностная плотность заряда, нКл/м2	Линейная плотность заряда, нКл/м	Объемная плотность заряда, нКл/м3	Точеч­ный заряд, нКл	Расстояние от центра симметрии фигуры до точек, ri м
R1	R2	R3	s1	s2	s3	t1	t2	t3	r1	q	r1	r2	r3
	Три концентрические сферы	0,1	0,2	0,3		-20							0,05	0,15	0,4
	Три концентрические сферы	0,1	0,2	0,3	-10		-10						0,05	0,15	0,4
	Два коаксиальных бесконечных цилиндра	0,1	0,2						-5				0,05	0,15	0,3
	Два коаксиальных бесконечных цилиндра	0,1	0,2			-8							0,05	0,15	0,3
	Три коаксиальных бесконечных цилиндра	0,1	0,2	0,3					-10	-20			0,05	0,15	0,5
	Три коаксиальных бесконечных цилиндра	0,1	0,2	0,3	-10								0,05	0,15	0,5
	Две концентрические фигуры - шар окруженный сферой	0,1	0,4										0,05	0,2	0,5

Окончание таблицы 2.1

	Две концентрические фигуры - шар окруженный сферой	0,1	0,3			-30					-100		0,05	0,2	0,4
	Точечный заряд в центре сферы		0,3										0,1	0,2	0,4
	Точечный заряд в центре сферы		0,2			-10						-20	0,1	0,3	0,4
	Точечный заряд в центре двух концентрических сфер		0,3	0,5			-30					-10	0,2	0,4	0,6
	Точечный заряд в центре двух концентрических сфер		0,2	0,4		-20							0,1	0,3	0,5
	Две бесконечные параллельные плоскости	Находятся на расст. 0,02 м друг от друга		-30							Слева от I пл.	Между пл.	Справа от II пл.
	Две бесконечные параллельные плоскости	Находятся на расст. 0,01 м друг от друга	-10	-20							Слева от I пл.	Между пл.	Справа от II пл.
	Три бесконечные параллельные плоскости	Находятся на расст. 0,02 м друг от друга	-10								Слева от I пл.	Между I и II пл	Справа от II пл.
	Три бесконечные параллельные плоскости	Находятся на расст. 0,01 м друг от друга		-10							Слева от I пл.	Между II и III пл	Справа от III пл.

Схема к вариантам 1, 2	Схема к вариантам 3, 4
Схема к вариантам 5, 6	Схема к вариантам 7, 8
Схема к вариантам 9, 10	Схема к вариантам 11, 12
Схема к вариантам 13, 14	Схема к вариантам 15, 16

Рис. 2.3. Схемы расположения фигур

Пример решения задачи

Источники тока с электродвижущими силами E₁ и E₂ включены в цепь, как показано на рис. 3.2. Определить силы токов, текущих в сопротивлениях R₁, R₂ и R₃, если E₁ = 2,1 В; E₂ = 1,9 В; R₁ = 45 Ом; R₂ = 10 Ом; R₃ = 10 Ом. Сопротивлениями источников пренебречь.

Рис. 3.2. Схема электрической цепи

Решение.Силы токов в разветвленной цепи определяются с помощью законов Кирхгофа. Чтобы найти три значения силы токов, следует составить три уравнения. Выберем направления токов, как они показаны на рис. 3.2 и условимся обходить контуры по часовой стрелке. Рассматриваемая задача имеет два узла А и В. Но составлять уравнение по первому закону Кирхгофа следует только для одного узла, так как уравнение, составленное для второго узла, будет следствием первого уравнения.

При составлении уравнений по первому закону Кирхгофа необходимо соблюдать правило знаков: ток, подходящий к узлу, входит в уравнение со знаком плюс, ток, отходящий от узла, – со знаком минус.

По первому закону Кирхгофа для узла В имеем:

I₃ – I₁ – I₂ = 0. (3.4)

Недостающие два уравнения получим по второму закону Кирхгофа. Число независимых уравнений, которые могут быть составлены по второму закону Кирхгофа, также меньше числа контуров. Чтобы найти необходимое число независимых уравнений, следует придерживаться правила: выбирать контуры таким образом, чтобы в каждый новый контур входила хотя бы одна ветвь, не участвовавшая ни в одном из ранее использованных контуров.

При составлении уравнений по второму закону Кирхгофа необходимо соблюдать следующее правило знаков:

а) если ток по направлению совпадает с выбранным направлением обхода контура, то соответствующее произведение IR входит в уравнение со знаком плюс, в противном случае произведение IR входит в уравнение со знаком минус;

б) если ЭДС повышает потенциал в направлении обхода контура, т.е. если при обходе контура приходится идти от минуса к плюсу внутри источника, то соответствующая ЭДС входит в уравнение со знаком плюс, в противном случае – со знаком минус.

По второму правилу Кирхгофа имеет соответственно для контуров АR₁BR₂A и AR₃BR₁A:

I₂R₂ – I₁R₁ = –E₂, (3.5)

I₃R₃ + I₁R₁ = E₁. (3.6)

Подставив в уравнения значения сопротивлений и ЭДС, получим систему уравнений:

. (3.7)

Для решения системы удобно воспользоваться методом определителей (детерминантов). С этой целью перепишем уравнения еще раз в следующем виде:

(3.8)

Искомые значения токов найдем из выражений

I₁ = D₁/D; I₂ = D₂/D; I₃ = D₃/D, (3.9)

где D – определитель системы уравнений, D₁, D₂, D₃ – определители, полученные заменой соответствующих столбцов определителя D столбцами, составленными из свободных членов трех вышеприведенных уравнений.

(3.10)

(3.11)

(3.12)

(3.13)

Отсюда получаем: I₁ = 0,04 A, I₂ = –0,01 A, I₃ = 0,03 A.

Знак минус у значения силы тока I₂ свидетельствует о том, что при произвольном выборе направлений токов, указанных на рисунке, направление тока I₂ было указано противоположно истинному. На самом деле ток I₂ течет от узла А к узлу В.

3.3 Задание для самостоятельного выполнения по вариантам

N источников токов c э.д.с. Е_n, имеющие внутренние сопротивления r_n и реостаты R_k соединены как показано на рис. 3.3 (см. свой вариант). Вычислить силы токов I_k, текущих через реостаты. Данные приведены в табл. 3.1.

Значения величин. Таблица 3.1

№ варианта	Е1, В	Е2, В	Е3, В	r1, Ом	r2, Ом	r3, Ом	R1, Oм	R2, Oм	R3, Oм

вариант 1	вариант 2	вариант 3
вариант 4	вариант 5	вариант 6
вариант 7	вариант 8	вариант 9

Рис. 3.3. Схемы электрических цепей

вариант 10	вариант 11	вариант 12
вариант 13	вариант 14	вариант 15
вариант 16

Продолжение рис. 3.3. Схемы электрических цепей

Закон Био-Савара-Лапласа

или (4.3)

где – магнитная индукция поля, создаваемого элементом провода длиной dl с током I;

– радиус-вектор, направленный от элемента проводника к точке, в которой определяется магнитная индукция;

a – угол между радиусом-вектором и направлением тока в элементе провода.

Магнитная индукция в центре кругового тока определяется по формуле:

, (4.4)

где R – радиус кругового витка.

Магнитная индукция на оси кругового тока определяется по формуле:

, (4.5)

где h – расстояние от центра витка до точки, в которой определяется магнитная индукция.

Магнитная индукция поля прямого тока определяется по формуле:

, (4.6)

где r₀ – расстояние от оси провода до точки, в которой определяется магнитная индукция.

Магнитная индукция поля, создаваемого отрезком провода с током (рис. 4.1) определяется по формуле:

(4.7)

Рис. 4.1. Отрезок провода с током

Направление вектора магнитной индукции 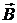обозначено точкой – это значит, что 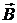направлен перпендикулярно плоскости чертежа к нам.

При симметричном расположении концов провода относительно точки, в которой определяется магнитная индукция – cos a₂ = cos a₁ = cos a, тогда

(4.8)

Магнитная индукция поля соленоида определяется по формуле:

B = mm₀nI, (4.9)

где n – отношение числа витков соленоида к его длине.

Пример решения задачи

Бесконечно длинный провод изогнут так, как это изображено на рис. 4.2а. Радиус R дуги окружности равен 10 см. Определить магнитную индукцию В поля, создаваемого в точке О током I = 80 A, текущим по этому проводу.

Решение. Магнитную индукцию 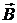в точке О найдем, используя принцип суперпозиции магнитных полей: . В нашем случае провод можно разбить на три части (рис. 4.2б): два прямолинейных провода (1 и 3), одним концом уходящие в бесконечность, и дугу полуокружности (2) радиуса R. Тогда

, (4.10)

где , – магнитные индукции в точке О, создаваемые током, текущим соответственно на первом, втором и третьем участках провода.

а б

Рис. 4.2. Проводник с током

Так как точка О лежит на оси провода 1, то В₁ = 0 и тогда

(4.11)

Учитывая, что векторы и направлены в соответствии с правилом буравчика перпендикулярно плоскости чертежа от нас, то геометрическое суммирование можно заменить алгебраическим:

B = B₂ + B₃. (4.12)

Магнитную индукцию B₂ найдем, воспользовавшись выражением для магнитной индукции в центре кругового тока:

. (4.13)

В нашем случае магнитное поле в точке О создается лишь половиной такого кругового тока, поэтому

. (4.14)

Магнитную индукцию В₃ найдем, воспользовавшись соотношением:

. (4.15)

В нашем случае r₀ = R, a₁ = p/2 (сos a₁ = 0), a₂ ® p (сos a₂ = –1). Тогда

. (4.16)

Используя найденные выражения для В₂ и В₃, получим

или (4.17)

Выполним проверку единиц измерения величин.

(4.18)

Произведем вычисления:

Тл.

4.3 Задание для самостоятельного выполнения по вариантам

Бесконечно длинный тонкий проводник с током I = 100 А изогнут так, как показано на рис. 4.3. Радиус изгиба R = 10 см. Определить в точке О магнитную индукцию поля В, создаваемого этим током. Направление тока показано на рисунке стрелкой.

вариант 1	вариант 2	вариант 3
вариант 4	вариант 5	вариант 6

Рис. 4.3. Формы проводников с током

вариант 7	вариант 8	вариант 9
вариант 10	вариант 11	вариант 12
вариант 13	вариант 14	вариант 15	вариант 16

Продолжение рис. 4.3. Формы проводников с током

Пример решения задачи

Рассмотрев фотографию треков заряженных частиц, двигавшихся в магнитном поле определить отношение заряда к массе неизвестной частицы, а также знак заряда этой частицы, если известно, что левый трек принадлежит ядру атома водорода, правый неизвестной частице. Отношение заряда атома водорода к его массе равно 9,6×10⁷ Кл/кг. Модули начальных скоростей частиц одинаковы. Индукция магнитного поля 2,2 Тл. Направление магнитного поля показано на рис. 5.1.

Решение. Для решения этой задачи оба трека осторожно переносят на кальку или делают ксерокопию рисунка. Затем измеряют радиусы кривизны треков. Для этого вначале находят центры кривизны. В средних участках треков проводят по две хорды и в середине к ним восстанавливают перпендикуляры. Точки пересечения перпендикуляров будут центрами кривизны треков. Затем измеряют радиусы кривизны с помощью измерительной линейки, учитывая масштаб снимка.

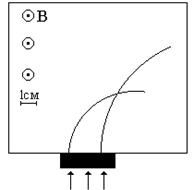
Рис. 5.1. Треки заряженных частиц в магнитном поле

Для нашего случая R₁ = 0,032 м, R₂ = 0,072 м.

На заряженную частицу, движущуюся в магнитном поле, действует сила Лоренца, вектор которой перпендикулярен вектору скорости частицы. Эта сила является центростремительной силой:

F_л = quB, 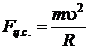, F_л = F_ц.с., (5.4)

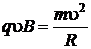. (5.5)

Отсюда модуль скорости неизвестной частицы u₁ будет равен:

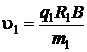, (5.6)

где q₁ – заряд частицы;

m₁ – масса частицы;

R₁ – радиус кривизны трека;

B – модуль магнитной индукции.

Модуль скорости ядра атома водорода u₂ равен:

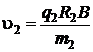, (5.7)

где q₂ – заряд ядра водорода;

m₂ – масса ядра атома водорода;

R₂ – радиус кривизны трека.

Так как по условию u₁ = u₂, то

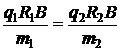. (5.8)

Отсюда получаем:

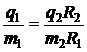. (5.9)

Подставляя в последнюю формулу числовые данные, находим:

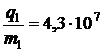Кл/кг.

Выполним проверку единиц измерения величин.

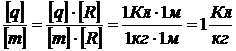. (5.10)

Воспользовавшись правилом левой руки определяем, что наша частица заряжена положительно.

5.3 Задание для самостоятельного выполнения по вариантам

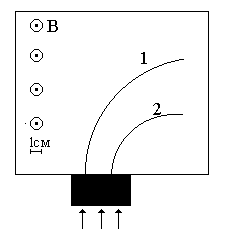
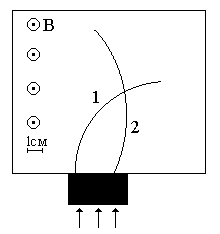
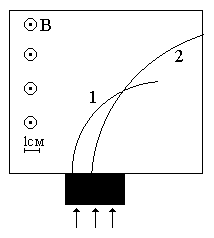
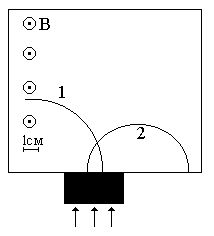
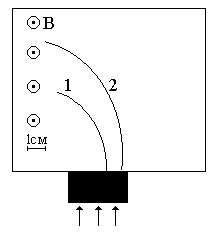
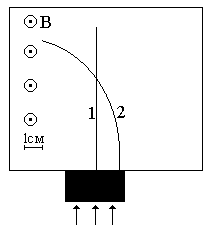
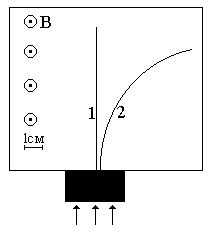
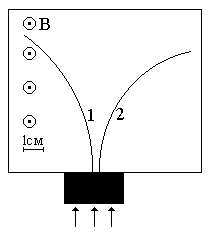
Неизвестные частицы 1 и 2 (см. рис. 5.2) прошли ускоряющую разность потенциалов U и влетели перпендикулярно линиям магнитной индукции В в камеру Вильсона. По фотографии трека определите удельный заряд частиц q/m и укажите знаки их заряда. При измерении радиусов треков учитывайте масштаб снимка, указанный на рис. 5.2. Направление линий магнитной индукции указано на рисунке обозначением:  – перпендикулярно листу бумаги "к нам", Ä – перпендикулярно листу бумаги "от нас". Данные приведены в табл. 5.1.

Таблица 5.1

Значения величин.

№ варианта	U, B	В, Tл
		2,1
		2,2
		2,3
		2,4
		2,5
		2,6
		2,7
		2,8
		2,9
		3,0
		3,1
		3,2
		3,3
		3,4
		3,5

вариант 1	вариант 2
вариант 3	вариант 4
вариант 5	вариант 6

Рис. 5.2. Треки частиц в магнитном поле

вариант 7	вариант 8
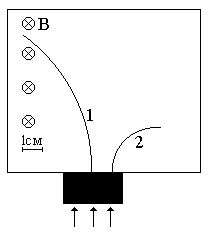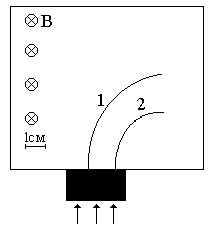вариант 9	вариант 10
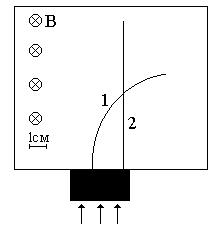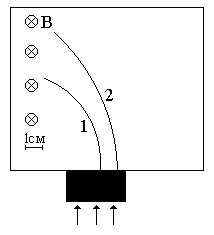вариант 11	вариант 12

Продолжение рис. 5.2. Треки частиц в магнитном поле

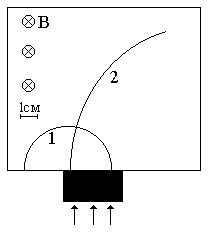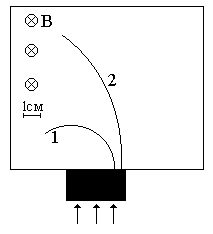вариант 13	вариант 14
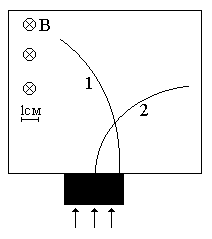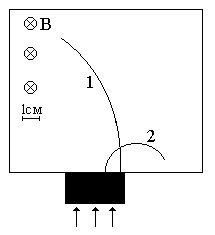вариант 15	вариант 16

Продолжение рис. 5.2. Треки частиц в магнитном поле

Пример решения задачи

Обмотка соленоида состоит из одного слоя плотно прилегающих друг к другу витков медного провода диаметром d = 0,2 мм. Диаметр D соленоида равен 5 см. По соленоиду течет ток I = 1 А. Определить количество электричества Q, протекающее через обмотку, если концы ее замкнуты накоротко. Толщиной изоляции пренебречь.

Решение. Количество электричества dQ, которое протекает по проводнику за время dt при силе тока I, определяется равенством:

dQ = I dt. (6.8)

Полное количество электричества, протекающее через проводник за время t, будет Сила тока в данном случае убывает экспоненциально со временем и выражается формулой:

(6.9)

Внося выражение силы тока I под знак интеграла и интегрируя от 0 до ¥ (при t