Циклы паротурбинных и холодильных установок

14.4; 14.6; 15.1; 15.8; 15.13

14.4 Паротурбинная установка работает по циклу Ренкина с начальными параметрами р₁ = 10 МПа и t₁ = 530 ⁰С. Давление в конденсаторе р₂ = 40 гПа. Определите термический КПД цикла Ренкина и сравните его с термическим КПД цикла Карно в том же интервале температур.

Решение.

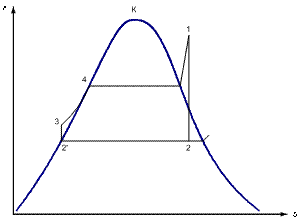
Термический КПД цикла Ренкина:

,

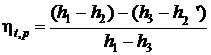где h₁ – энтальпия пара перед турбиной;

h₂ – энтальпия пара на входе в конденсатор;

h₂^’ – энтальпия воды на выходе из конденсатора;

h₃ – энтальпия воды после насоса (энтальпия питательной воды).

Термический КПД цикла Карно:

,

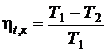где Т₁ – температура теплоисточника;

Т₂ – температура холодного источника.

Используя [5, табл. III, с.58] определяем при р₁ = 10 МПа и температуре t₁ = 530 ⁰С, что h₁ = 3451,7 кДж/кг, s₁ = 6,6965 кДж/(кг·К).

s₁ = s₂

Используя [5, табл. II, с.24] определяем

р₂ = 40 гПа = 4·10³ Па. При этом давлении ;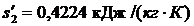

;

;

.

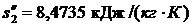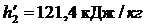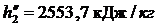t₂ = 28,96 ⁰C.

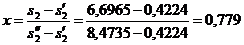
Энтальпия пара на входе в конденсатор:

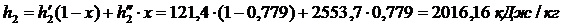
Энтальпия воды на выходе из конденсатора: 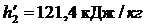и энтропия .

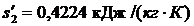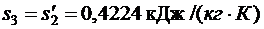
Используя [5, табл. III, с.57] при р₁ = 10 МПа определяем, что наше значение 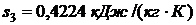находится между значениями 0,2944 кДж/(кг·К) и 0,4337 кДж/(кг·К) [5, табл. III, с.57], что соответствует температурам 20 ⁰С и 30 ⁰С. Значит, искомая температура t₃ находится в пределах от 20 ⁰С до 30 ⁰С. Проинтерполируем:

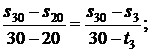
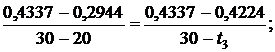откуда t₃ = 29,19 ⁰C.

Тогда для энтальпии

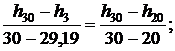
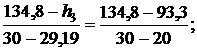откуда h₃ = 131,44 кДж/кг

Термический КПД цикла Ренкина:

.

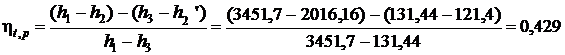Термический КПД цикла Карно:

.

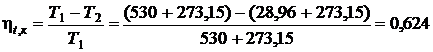Ответ: ; .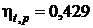

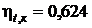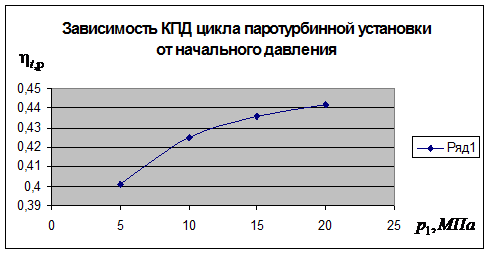
14.6 При одинаковой начальной температуре t₁ = 500 ⁰C постройте кривую зависимости 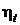цикла паротурбинной установки от начального давления р₁, приняв его равным 5,0; 10,0; 15,0 и 20,0 МПа. Давление в конденсаторе одинаково, р₂ = 40 гПа. Учтите работу питательного насоса. Представьте циклы в T,s – диаграмме.

Решение.

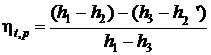
1) Используя [5, табл. III, с.54] определяем при р₁ = 5 МПа и температуре t₁ = 500 ⁰С, что h₁ = 3434,5 кДж/кг, s₁ = 6,9778 кДж/(кг·К).

s₁ = s₂

Используя [5, табл. II, с.24] определяем

р₂ = 40 гПа = 4·10³ Па. При этом давлении ;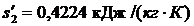

;

;

.

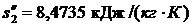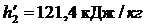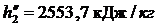t₂ = 28,96 ⁰C.

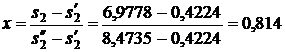
Энтальпия пара на входе в конденсатор:

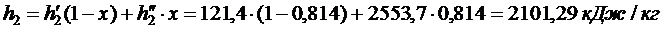Энтальпия воды на выходе из конденсатора: 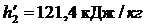и энтропия .

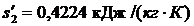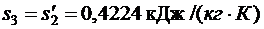
Используя [5, табл. III, с.53] при р₁ = 5 МПа определяем, что наше значение 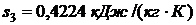находится между значениями 0,2955 кДж/(кг·К) и 0,4353 кДж/(кг·К) [5, табл. III, с.53], что соответствует температурам 20 ⁰С и 30 ⁰С. Значит, искомая температура t₃ находится в пределах от 20 ⁰С до 30 ⁰С. Проинтерполируем:

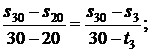
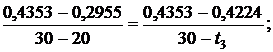откуда t₃ = 29,08 ⁰C.

Тогда для энтальпии

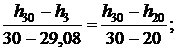
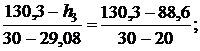откуда h₃ = 126,46 кДж/кг

Термический КПД цикла Ренкина:

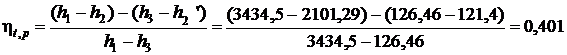
2) Используя [5, табл. III, с.58] определяем при р₁ = 10 МПа и температуре t₁ = 500 ⁰С, что h₁ = 3375,1 кДж/кг, s₁ = 6,5993 кДж/(кг·К).

s₁ = s₂

Используя [5, табл. II, с.24] определяем

р₂ = 40 гПа = 4·10³ Па. При этом давлении ;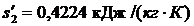

;

;

.

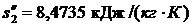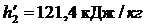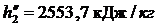t₂ = 28,96 ⁰C.

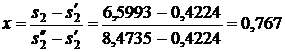
Энтальпия пара на входе в конденсатор:

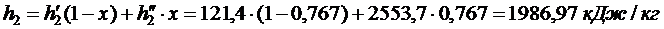Энтальпия воды на выходе из конденсатора: 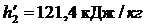и энтропия .

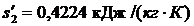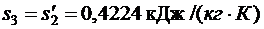
Используя [5, табл. III, с.57] при р₁ = 10 МПа определяем, что наше значение 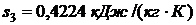находится между значениями 0,2944 кДж/(кг·К) и 0,4337 кДж/(кг·К) [5, табл. III, с.57], что соответствует температурам 20 ⁰С и 30 ⁰С. Значит, искомая температура t₃ находится в пределах от 20 ⁰С до 30 ⁰С. Проинтерполируем:

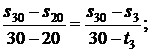
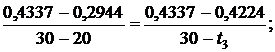откуда t₃ = 29,19 ⁰C.

Тогда для энтальпии

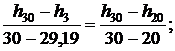
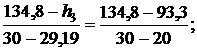откуда h₃ = 131,44 кДж/кг

Термический КПД цикла Ренкина:

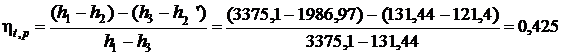
3) Используя [5, табл. III, с.64] определяем при р₁ = 15 МПа и температуре t₁ = 500 ⁰С, что h₁ = 3310,8 кДж/кг, s₁ = 6,3479 кДж/(кг·К).

s₁ = s₂

Используя [5, табл. II, с.24] определяем

р₂ = 40 гПа = 4·10³ Па. При этом давлении ;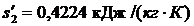

;

;

.

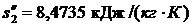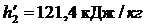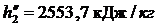t₂ = 28,96 ⁰C.

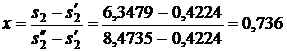
Энтальпия пара на входе в конденсатор:

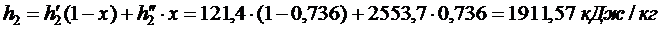Энтальпия воды на выходе из конденсатора: 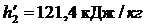и энтропия .

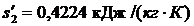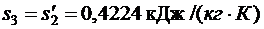
Используя [5, табл. III, с.63] при р₁ = 15 МПа определяем, что наше значение 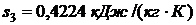находится между значениями 0,2932 кДж/(кг·К) и 0,4322 кДж/(кг·К) [5, табл. III, с.63], что соответствует температурам 20 ⁰С и 30 ⁰С. Значит, искомая температура t₃ находится в пределах от 20 ⁰С до 30 ⁰С. Проинтерполируем:

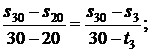
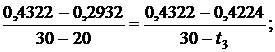откуда t₃ = 29,29 ⁰C.

Тогда для энтальпии

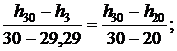
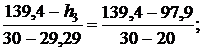откуда h₃ = 136,45 кДж/кг

Термический КПД цикла Ренкина:

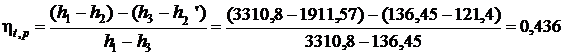
4) Используя [5, табл. III, с.66] определяем при р₁ = 20 МПа и температуре t₁ = 500 ⁰С, что h₁ = 3241,2 кДж/кг, s₁ = 6,1445 кДж/(кг·К).

s₁ = s₂

Используя [5, табл. II, с.24] определяем

р₂ = 40 гПа = 4·10³ Па. При этом давлении ;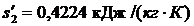

;

;

.

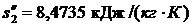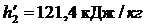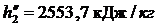t₂ = 28,96 ⁰C.

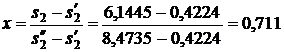
Энтальпия пара на входе в конденсатор:

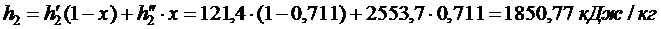Энтальпия воды на выходе из конденсатора: 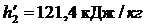и энтропия .

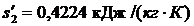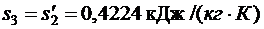
Используя [5, табл. III, с.65] при р₁ = 20 МПа определяем, что наше значение 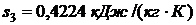находится между значениями 0,2921 кДж/(кг·К) и 0,4306 кДж/(кг·К) [5, табл. III, с.65], что соответствует температурам 20 ⁰С и 30 ⁰С. Значит, искомая температура t₃ находится в пределах от 20 ⁰С до 30 ⁰С. Проинтерполируем:

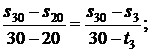
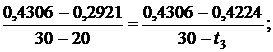откуда t₃ = 29,41 ⁰C.

Тогда для энтальпии

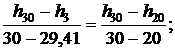
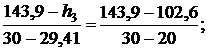откуда h₃ = 141,46 кДж/кг

Термический КПД цикла Ренкина:

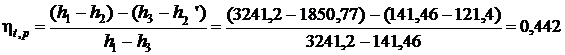
Ответ: р₁, МПа 5 10 15 20

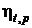0,401 0,425 0,436 0,442

15.1 Воздушная холодильная машина должна обеспечить температуру в охлаждаемом помещении t_охл = 5 ⁰C при температуре окружающей среды t_о.с. = 20 ⁰C. Холодопроизводительность машины 840 МДж/ч. Давление воздуха на выходе из компрессора р₂ = 0,5 МПа, давление в холодильной камере р₁ = 0,1 МПа. Определите мощность двигателя для привода машины, расход воздуха, холодильный коэффициент и количество теплоты, передаваемое окружающей среде. Подсчитайте холодильный коэффициент машины, работающей по циклу Карно в том же интервале температур. Представьте цикл в T,s – диаграмме.

Решение. Холодильный коэффициент: .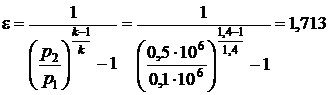

Мощность двигателя для привода машины: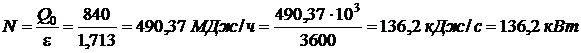

Холодильный коэффициент машины, работающей по циклу Карно: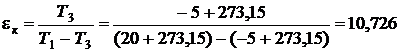

Количество теплоты, передаваемое окружающей среде: 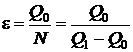, откуда .

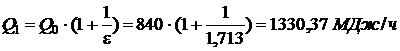Удельная холодопроизводительность: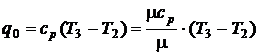

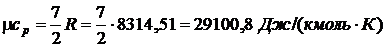[3, с.36]

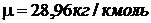
Из соотношения 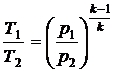находим .

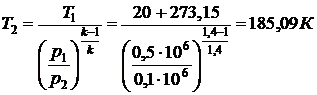Тогда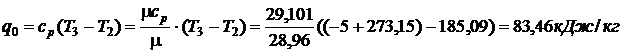

Расход воздуха: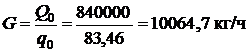

Ответ: ; ; ; ; .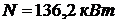

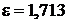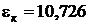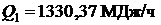15.8 Компрессор аммиачной холодильной установки имеет теоретическую мощность 40 кВт. Из компрессора сухой насыщенный пар аммиака при температуре t₂ = 25 ⁰C направляется в конденсатор, после которого жидкость в дроссельном вентеле расширяется. Температура испарения аммиака в охлаждаемой среде t₁ = -10 ⁰C. Определите холодопроизводительность установки, используя табл. 24 приложения [3].

Решение. Холодопроизводительность установки: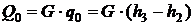

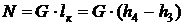, откуда 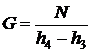, тогда

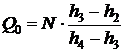
Процесс 1-2 – дросселирование ( )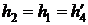

Процесс 3-4 – адиабатное сжатие ( )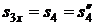

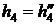находим по таблице 24 при t = 25 ⁰C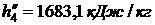

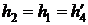находим по таблице 24 при t = 25 ⁰C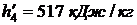

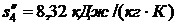определяли по таблице 24 при t = 25 ⁰C

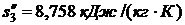определяли по таблице 24 при t = -10 ⁰C

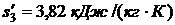определяли по таблице 24 при t = -10 ⁰C

Степень сухости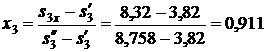

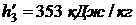определяли по таблице 24 при t = -10 ⁰C

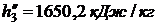определяли по таблице 24 при t = -10 ⁰C

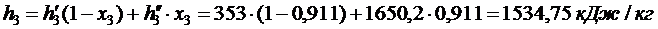
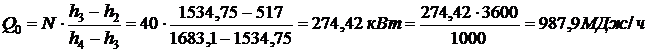Ответ: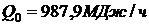

15.13 Современные электрогенераторы работают с применением водородного охлаждения. Циркулирующий в системе водород может быть использован как рабочее вещество в схеме теплового насоса (рис. 15.6). Каков отопительный коэффициент 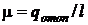этой установки, если давление водорода в системе охлаждения генератора постоянно: р₁ = р₄ = 0,097 МПа, а температура в точках 1,3 и 4 указана на схеме.

Каково давление водорода р₂ поступающего в теплообменник. Теплоемкость с_р водорода считать не зависящей от температуры.

Решение. Отопительный коэффициент .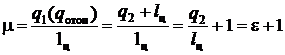

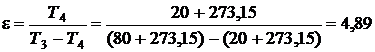. Тогда .

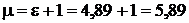Подставив значения в формулу 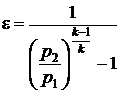, получим 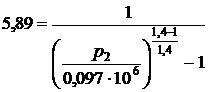откуда р₂ = 186041 Па = 0,186 МПа.

Ответ: 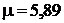; р₂ = 0,186 МПа.

б) Теплопередача [4]