Расчет удельных механических нагрузок от внешнего воздействия метеорологических факторов и сил тяжести на провода и тросы с учетом их высоты крепления на промежуточной опоре.

Определим постоянно действующие вертикальные нагрузки на провод и трос, возникающие под действием силы тяжести самого провода и троса:

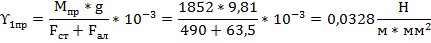
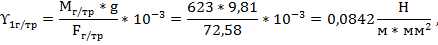
Где 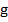- ускорение свободного падения, 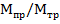- масса провода/троса, 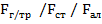- сечения троса/стали/алюминия.

Определим временно действующую вертикальную нагрузку на провод, появляющуюся под действием силы тяжести гололеда:

,

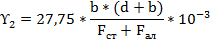
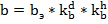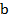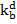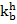Где - расчетная толщина стенки гололеда, и - коэффициенты учитывающие отличие диаметра провода от 10 мм и высоты подвеса провода от 10 м. Для их определения необходимо знать диаметр провода и высоту расположения приведенного центра тяжести всей системы проводов.

Определим высоту приведенного центра тяжести системы проводов (эскиз пролета представлен на рисунке 3.1):

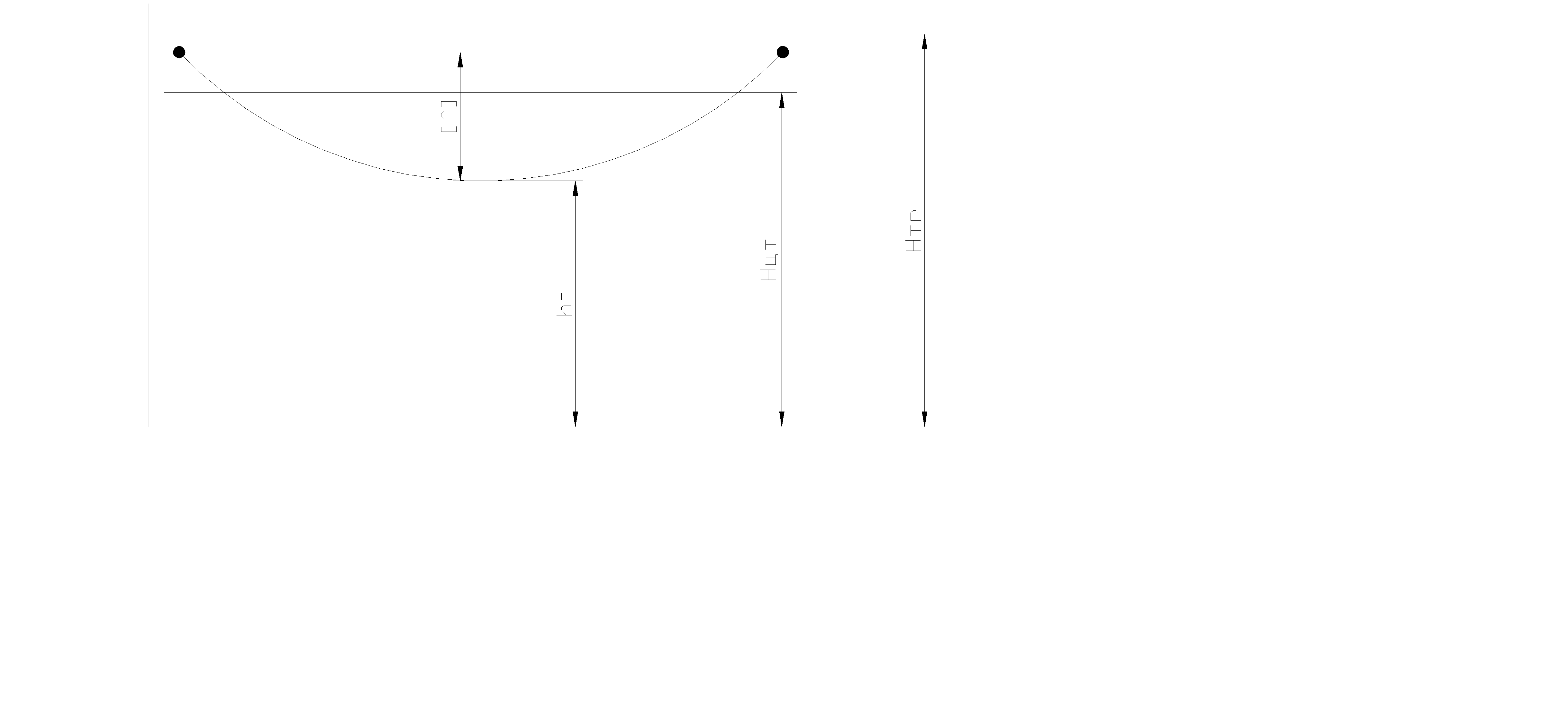
Рисунок 3.1. Эскиз пролета.

Допустимое значение стрелы провеса провода

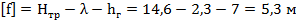
Высота центра тяжести провода:

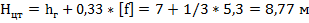
Высота приведенного центра тяжести системы проводов:

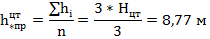
При высоте центра тяжести системы проводов менее 14,3 м значение коэффициента .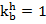

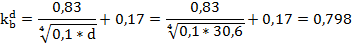
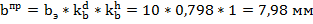
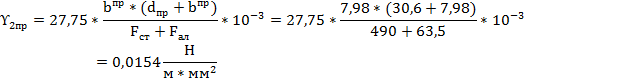
Определим временно действующую вертикальную нагрузку на трос, появляющуюся под действием силы тяжести гололеда:

Высота центра тяжести троса:

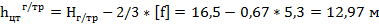
Высота приведенного центра тяжести системы тросов:

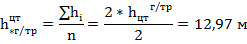
Поскольку высота центра тяжести системы тросов менее 14,3 м, то значения поправочного коэффициента .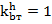

Рассчитаем поправочный коэффициент на толщину стенки гололеда в зависимости от диаметра троса, отличного от 10 мм:

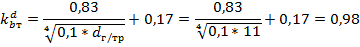
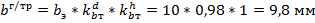
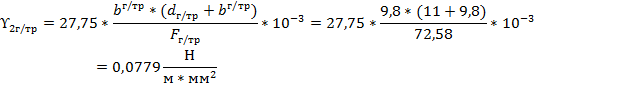
Определим вертикальную нагрузку, возникающую под действием силы тяжести провода (троса) при гололеде:

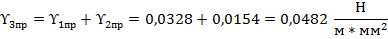
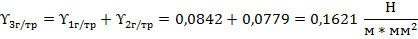
Определим временную горизонтальную нагрузку, возникающую вследствие давления ветра на провода, свободные от гололеда:

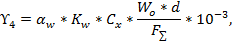
где:

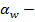поправочный коэффициент, учитывающий неравномерность распределения ветрового давления на провода вдоль пролета. Зависимость этого коэффициента от давления ветра представлена на рисунке 3.2.

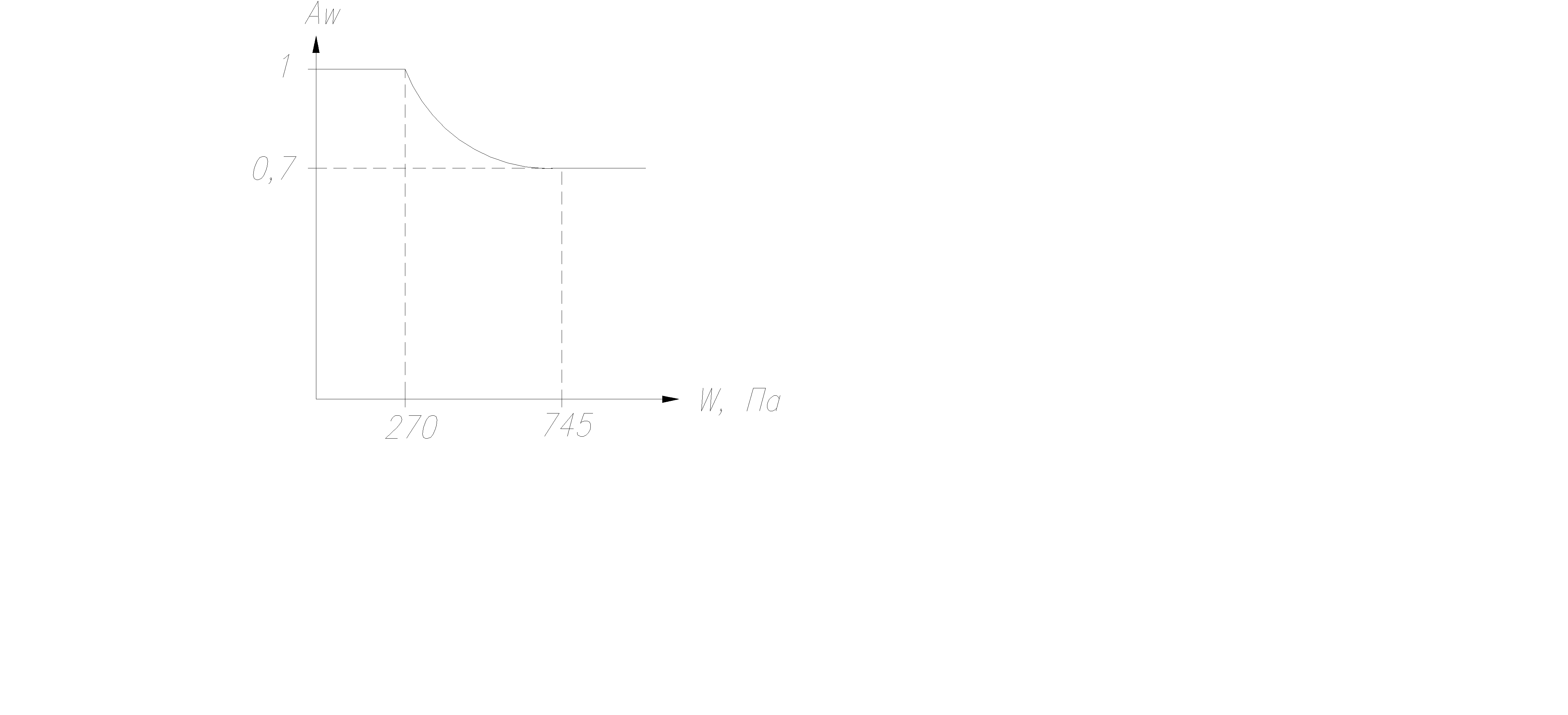Рисунок 3.2. Зависимость поправочного коэффициента 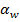от ветрового давления.

Гиперболическую часть данного графика описывает следующее аналитическое выражение:

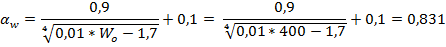
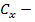аэродинамический коэффициент лобового сопротивления (равен 1,1 при диаметре проводов более 20 мм и 1,2 при диаметре проводов менее 20 мм). В нашем случае при 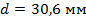, этот коэффициент принимает значение 1,1 [1].

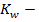коэффициент, учитывающий усиление ветрового давления при высоте подвеса проводов выше 10 м ( 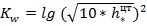при высоте центра тяжести проводов более 10 м; в противном случае он равен 1). В нашем случае этот коэффициент равен 1 для провода (значения для троса см. ниже).

На основании определенных выше поправочных коэффициентах можем определить значение :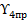

Определим значение :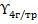

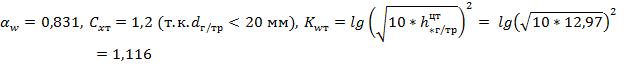
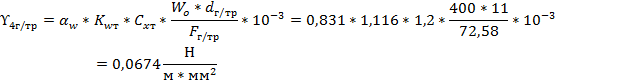
Определим временную горизонтальную нагрузку, возникающую вследствие ветрового давления на провод и трос покрытый гололедом:

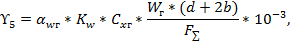
где коэффициенты 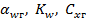имеют аналогичный физический смысл, изменятся лишь численное значение коэффициента 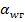и коэффициента :

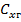Максимальная скорость ветра в условиях гололеда принимается в два раза меньше максимальной скорости ветра без гололеда [3]:

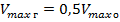
Ветровое давление пропорционально квадрату скорости ветра, значит при нормативной толщине стенки гололеда 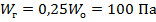. Это необходимо учесть при использовании зависимости, представленной на рисунке 3.2. Отсюда .

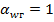Согласно [3] значения аэродинамического коэффициента лобового сопротивления для провода, покрытого гололедом необходимо принимать равным 1,2.

Исходя из вышесказанного, определим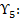

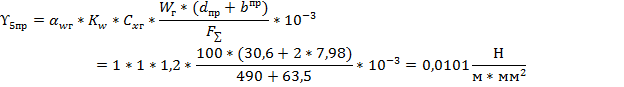
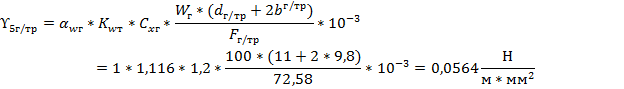
Определим суммарную нагрузку, возникающую вследствие совместного воздействия на провод горизонтальных и вертикальных сил в условиях отсутствия гололеда:

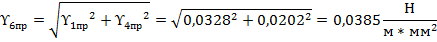
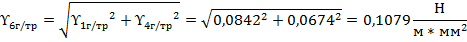
Определим суммарную нагрузку, возникающую вследствие совместного воздействия на провод горизонтальных и вертикальных сил в условиях гололеда:

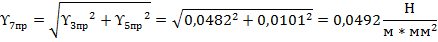
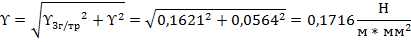
На основании данного сравнения выяснилось, что условия гололеда являются более жесткими и для провода и для троса. Вследствие этого принимаем наибольшими распределенными нагрузками значения нагрузок 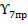и .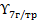

Построить зависимости среднеэксплуатационного напряжения в проводе от длины пролета, определить значения критических пролетов и выбрать определяющее по прочности провода нормативное сочетание климатических условий, основываясь на нормируемых значениях допустимых напряжений и эквивалентных физико-математических параметрах.

Уравнение состояния провода в форме записи относительно напряжений:

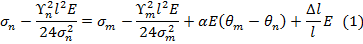
Расчет выполняется для анкерных пролетов различной длины, поэтому 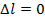, следовательно, слагаемое 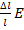в уравнении состояния провода отсутствует.

3.1. В качестве исходных условий принимается нормативное сочетание климатических условий, соответствующее наибольшей механической нагрузке.

Для провода АС 500/64 облегченной констпукции: 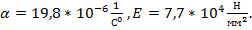Тогда,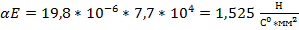

Исходные условия – нормативное сочетание климатических условий (НСКУ) при наибольшей нагрузке:

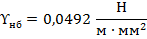
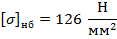
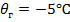
Искомые условия – среднеэксплуатационные:

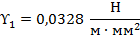
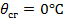
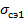
Уравнение состояния провода в этом случае имеет следующий вид:

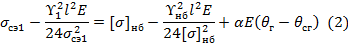
Уравнение состояния провода через коэффициенты А и В:

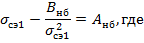
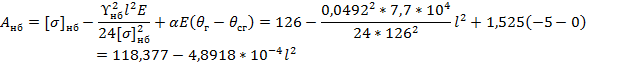
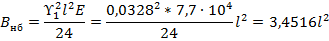
При 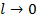уравнение состояния (2) становится вырожденным:

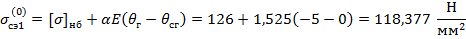
При 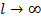уравнение состояния (2) также становится вырожденным:

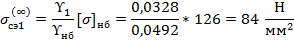
Расчет среднеэксплуатационных напряжений для каждой длины пролета выполняется итерационным методом Ньютона:

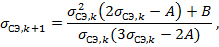
где k – номер текущей итерации. Расчет ведется до достижения заданной точности ξ =0,1 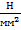, т.е. | 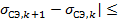0,1 .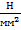

При :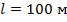

В качестве начального приближения среднеэксплуатационного напряжения принимается:

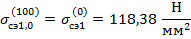
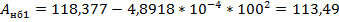
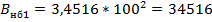
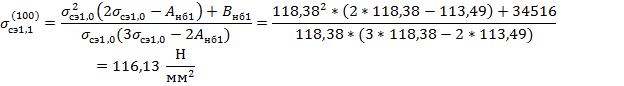
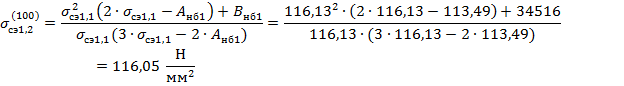
Необходимая точность расчета (0,1) достигнута.

Расчет среднеэксплуатационного напряжения для остальных длин пролетов сведен в таблицу 3.1.

Таблица 3.1. Зависимость среднеэксплуатационного напряжения от длины пролета, рассчитанная при исходных условиях, соответствующих НСКУ при наибольшей нагрузке.

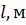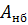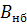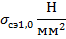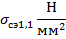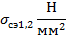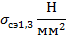	113,49		118,38	116,13	116,05
	98,81		116,05	110,66	110,19	110,18
	74,351		110,18	103,98	103,41	103,4
	40,108		103,4	98,168	97,823	97,821
	-3,918		97,821	94,067	93,916	93,915
	-57,73		93,915	91,371	91,309

3.2. В качестве исходных условий принимается нормативное сочетание климатических условий, соответствующее низшей температуре.

Исходные условия – нормативное сочетание климатических условий при низшей температуре:

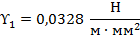
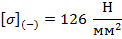
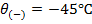
Искомые условия – среднеэксплуатационные:

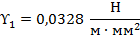
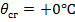
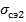
Уравнение состояния провода принимает вид:

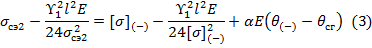
или

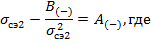
Коэффициенты:

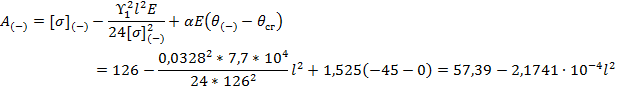
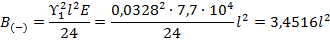
При 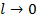уравнение состояния (3) становится вырожденным:

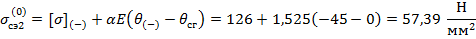
При 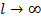уравнение состояния (3) также становится вырожденным:

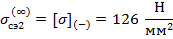
При :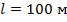

В качестве начального приближения среднеэксплуатационного напряжения принимается:

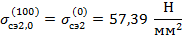
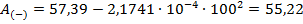
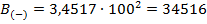
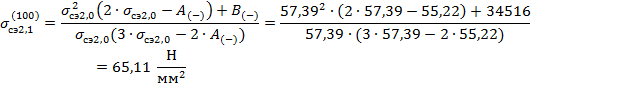
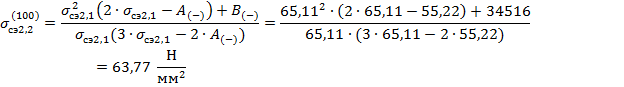
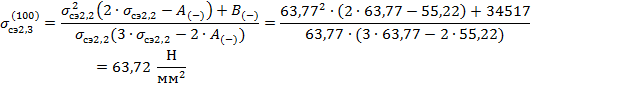
Необходимая точность расчета (0,1) достигнута.

Расчет среднеэксплуатационного напряжения для остальных длин пролетов сведен в таблицу 3.2.

Таблица 3.2. Зависимость среднеэксплуатационного напряжения от длины пролета, рассчитанная при исходных условиях, соответствующих НСКУ при низшей температуре.

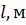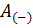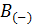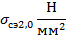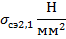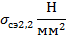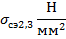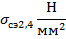	55,22		57,39	65,11	63,77	63,72
	48,69		63,72	76,62	74,07	73,95	73,94
	37,82		73,95	84,41	82,99	82,96
	22,6		82,96	91,06	90,32	90,31
	3,037		90,31	96,63	96,23	96,23
	-20,9		96,23	101,2	100,98	100,98

Зависимости среденэксплуатационного напряжения от длины пролета, построенные по данным таблиц 3.1.1 и 3.2.1, представлены на рисунке 3.1.

3.3. Зависимости СЭ напряжения в проводе от длины пролета, полученные при различных исходных НСКУ.

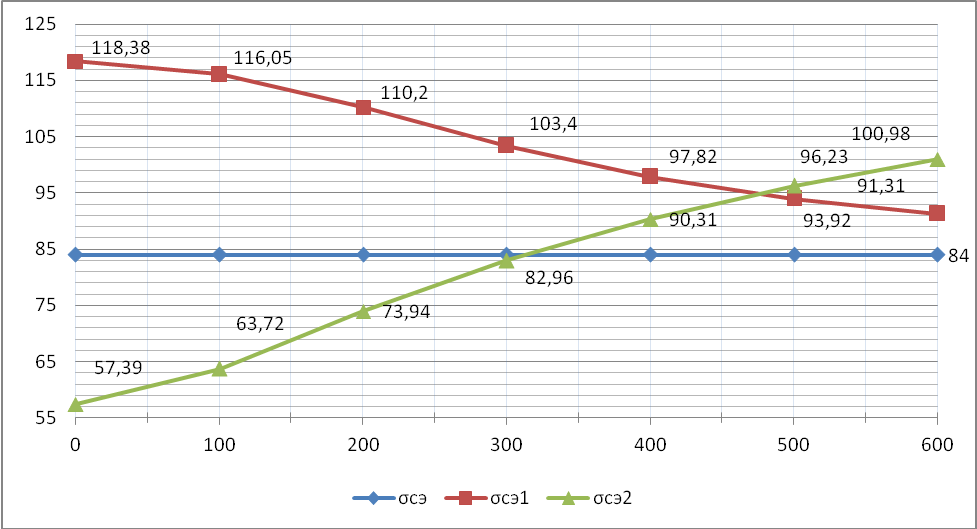
Рисунок 3.1. Зависимости среднеэксплуатационного напряжения при различных исходных НСКУ в зависимости от длины пролета

Выводы:

1. Из зависимостей, представленных на рисунке 3.1 видно, что при коротких пролетах (длинах пролета 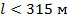) определяющим условием по прочности провода является нормативное сочетание климатических условий при низшей температуре.

2. При длинных пролетах (при длинах пролета 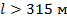) определяющим условием по прочности провода является нормативное сочетание климатических условий при .

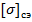3.4. Выбор определяющего по прочности провода НСКУ по методу критических пролетов.

При 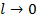и исходных условиях, соответствующих 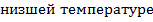, рассчитывается среднеэксплуатационное напряжение в проводе:

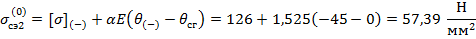
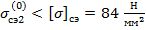, следовательно значение критического пролета 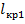является действительным. Расчет значения .

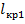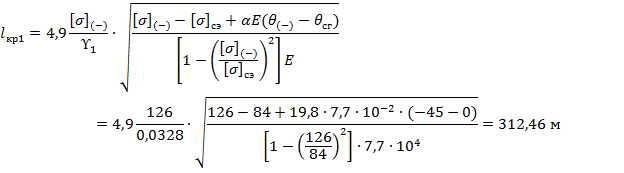
При 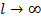и исходных условиях, соответствующих 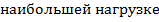, рассчитывается среднеэксплуатационное напряжение в проводе:

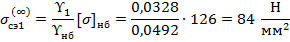
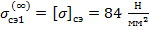, следовательно, значение критического пролета 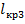является мнимым. Значит, его расчет нецелесообразен. При дальнейших расчетах будем полагать, что 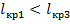( 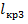принимаем равным 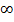). На основании данного допущения, расчет значения критического пролета 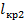не требуется. Приступаем к выбору определяющих по прочности провода условиям.

Выводы:

1. При 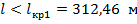определяющим по прочности провода является нормативное сочетание климатических условий при .

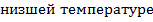2. При 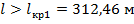определяющим по прочности провода является нормативное сочетание климатических условий при среднеэксплуатационных условиях.

Вычислив критическую температуру, установить нормативное сочетание климатических условий наибольшего провисания проводов и рассчитать габаритный пролет; построить шаблон для расстановки опор по продольному профилю трассы ВЛ с соблюдением масштабов: по вертикали – 1:500, по горизонтали – 1:5000.

4.1. Вычисление приблизительного значения критической температуры воздуха по оценочной формуле.

Оценочная формула:

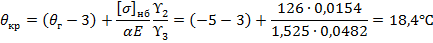
Производится сравнение критической температуры с высшей:

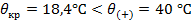
Из сравнения следует, что 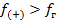, а, следовательно, стрела провеса провода в любом пролете будет больше при высшей температуре, без гололеда и без ветра, то есть под действием вертикальной нагрузки от собственной массы провода .

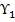Таким образом, габаритными климатическими условиями являются:

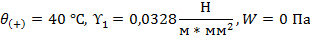
4.2. Расчет габаритного пролета.

Из пункта 3 известно, что при выборе определяющего по прочности нормативного сочетания климатических условий следует ориентироваться на значение :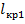

При 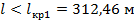определяющим по прочности провода является нормативное сочетание климатических условий при низшей температуре.

При 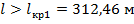определяющими по прочности провода являются среденэксплуатационные условия.

Так как точно не известно, к какому из двух интервалов принадлежит значение 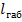, то расчет выполняется в соответствии с нижеследующим алгоритмом.

4.2.2. Предположим, что 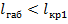и зададимся исходными условиями, соответствующими низшей температуре.

Исходные условия:

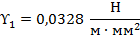
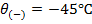
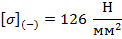
Искомые условия:

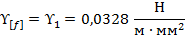
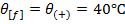
Величина габаритного пролета определяется из уравнения:

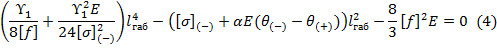
Уравнение состояния провода (4) через коэффициенты:

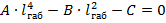
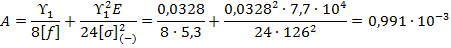
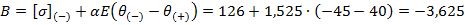
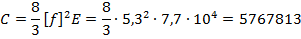
Решая биквадратное уравнение (4), получаем формулу для нахождения величины габаритного пролета:

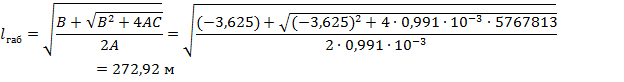
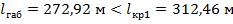, следовательно, определяющее по прочности провода нормативное сочетание климатических условий для 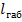совпадает с исходными условиями. Первая проверка выполняется.

4.2.3. Определение напряжения в низшей точке провода в габаритном пролете при габаритных климатических условиях.

Уравнение состояния провода:

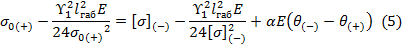
Уравнение состояния провода (5) через коэффициенты:

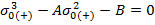
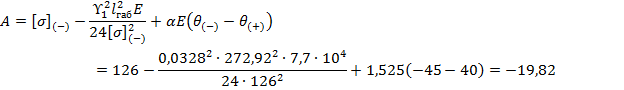
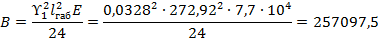
Расчет ведется по итерационному методу Ньютона:

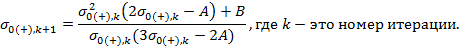
Расчет выполняется до заданной точности .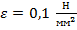

В качестве начального приближения принимается значение допустимого напряжения при среднеэксплуатационных условиях:

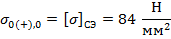
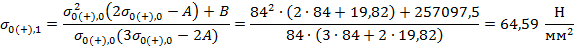
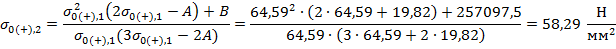
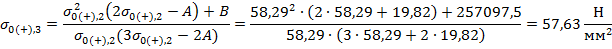
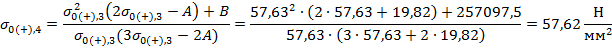
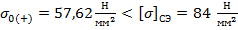, следовательно, начальное приближение выбрано верно.

4.2.4. Вычисление габаритной стрелы провеса.

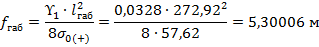
Δ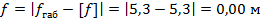

Поскольку разница между допустимой стрелой провеса провода и габаритной не превышает 0,02 м, то можно заключить, что габаритный пролет рассчитан верно.

4.2.5. Определение точного значения критической температуры воздуха.

Исходя из формулы для определения критической температуры, необходимо определить напряжение в низшей точке провода при нормативной толщине стенки гололеда в отсутствии ветра.

Уравнение состояния провода:

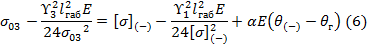
Уравнение состояния провода (6) через коэффициенты:

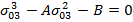
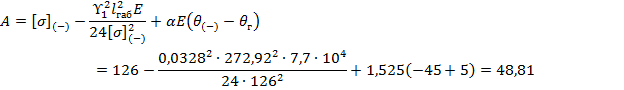
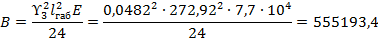
Расчет ведется по итерационному методу Ньютона:

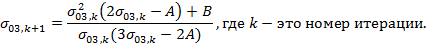
Расчет выполняется до заданной точности .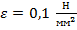

В качестве начального приближения принимается значение допустимого напряжения при наибольшей нагрузке:

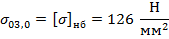
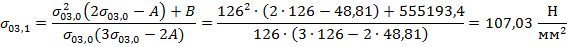
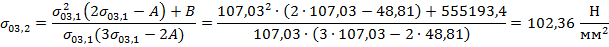
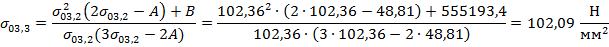
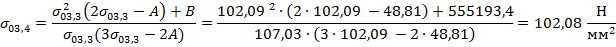
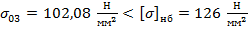, следовательно, начальное приближение выбрано верно.

Определим критическую температуру:

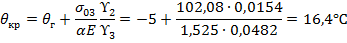
Погрешность при расчете критической температуры по оценочной формуле:

Δ 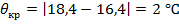, следовательно, можно сделать вывод, что оценочная формула работает с малой погрешностью.

4.3. Построение расстановочного шаблона.

Шаблон строится на основании расчета ординат кривой наибольшего провисания провода (т.е. при габаритных климатических условиях).

Значение абсциссы рассматривается в диапазоне :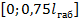

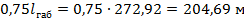
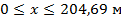
Коэффициент шаблона:

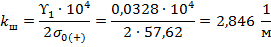
Уравнение кривой наибольшего провисания:

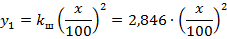
Уравнение габаритной кривой:

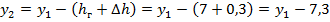
Где 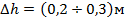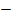монтажный запас.

Уравнение земляной кривой:

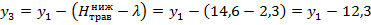
При :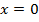

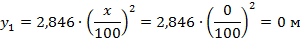
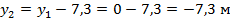
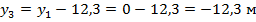
С учетом принятого масштаба:

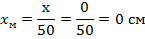
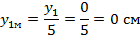
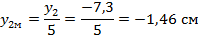
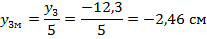
Результаты расчета остальных ординат сведены в таблицу 3.3.

Таблица 3.3. Координаты точек кривых расстановочного шаблона.

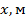			100,00	136,46			204,69
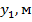		0,7115	2,846	5,2996	6,4035	11,384	11,92417
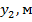	-7,3	-6,5885	-4,454	-2,0004	-0,8965	4,084	4,62417
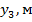	-12,3	-11,589	-9,454	-7,0004	-5,8965	-0,916	-0,37583
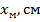				2,7292			4,0938
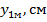		0,1423	0,5692	1,0599	1,2807	2,2768	2,384834
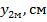	-1,46	-1,3177	-0,8908	-0,4001	-0,1793	0,8168	0,924834
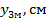	-2,46	-2,3177	-1,8908	-1,4001	-1,1793	-0,1832	-0,07517

При расстановке опор следует также учитывать, что длина пролета не должна превышать величины, допустимой по весовым и ветровым нагрузкам, на которые рассчитаны промежуточные опоры данного типа:

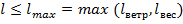
Принимается допущение, что:

Чертеж расстановочного шаблона представлен на рисунке 4.1.