Механика. Работа. Законы сохранения.
Задача 1. Поезд, идущий по горизонтальному участку со скоростью 36 км/ч, начинает двигаться равноускоренно и проходит 600 м, имеяв конце участи скорость 45 км/ч. Определить ускорение и время ускоренного движения.
Задача 2. Поезд идет со скоростью 108 км/ч. Пассажир этого поезда, сидящий у окна видит в течение 18 с встречный, длина которого 900 м. Определите скорость встречного поезда.
Задача 3. С вертолета упал камень и достиг Земли через 10 с. На какой высоте находился вертолет в начальныймомент, если: а) вертолет неподвижен; б) вертолет опускается со скоростью 5 м/с?
Задача 4. Тело, массой 10 кг находится на наклонной плоскости, составляющей угол 300 сгоризонтом. Коэффициент трения 0,6. Какую силу, направленную вдоль плоскости, нужно приложить к телу, чтобы перемещать его вниз по наклоннойплоскости с ускорением 2см/с2?
Задача 5. При каком ускорении разорвется трос, прочность которого на разрыв 15 кН, при вертикальном подъема груза массой 500 кг?
Задача 6. Льдина равномерной толщины плавает, выступая над уровнем воды на высоту 2 см. Найти массу льдины, если площадь ее основания 200 см, плотность льда 0,9×103 кг/м3? Плотность воды 1000 кг/м3.
Задача 7. Резиновый мяч массой m и радиусом R погружают в воду на глубину h и отпускают. На какую высоту, считая от поверхности воды, подпрыгнет мяч? Сопротивление воды и воздуха при движении не учитывать. Плотность воды r.
Задача 8. Орудие, имеющее массу ствола 500 кг, стреляет в горизонтальном направлении, масса снаряда 5 кг, его начальная скорость 460 м/с. При выстреле ствол откатывается на расстояние 40 см. Найти среднюю силу торможения, возникающую в механизме, тормозящем ствол.
Задача 9. Какую работу совершил мальчик, стоящий на гладком льду, сообщив санкам скорость 4 м/с относительно льда, если масса санок 4 кг, а масса мальчика 20 кг?
Задача 10. Тяжелый шарик, подвешенный на нерастяжимой и невесомой нити, имеющей длину l, отклоняют от вертикали на угол a и затем отпускают. Какую максимальную скорость V приобретет шарик?
Коллекция задач и их решений
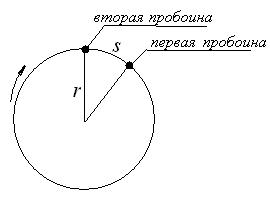
№1. Два бумажных диска насажены на общую горизонтальную ось так, что плоскости их параллельны и отстоят на d=30 см друг от друга. Диски вращаются с частотой n=25 с-1. Пуля, летевшая параллельно оси на расстоянии r=12 см от нее, пробила оба диска. Пробоины в дисках смещены друг относительно друга на расстояние s=5 см, считая по дуге окружности. Найти среднюю путевую скорость 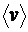 пули в промежутке между дисками и оценить создаваемое силой тяжести смещение пробоин в вертикальном направлении. Сопротивление воздуха не учитывать. [113 м/с; 35 мкм]
пули в промежутке между дисками и оценить создаваемое силой тяжести смещение пробоин в вертикальном направлении. Сопротивление воздуха не учитывать. [113 м/с; 35 мкм]
Дано:
d=0,3 м
n=25 с-1
r=0,12 м
s=0,05 м
Найти: 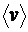 , l -?
, l -?
Решение.
Обозначим t – время движения пули между дисками. Тогда за время t: 1) пуля в горизонтальном направлении проходит расстояние d, 2) первая пробоина проходит путь s.
Имеем:
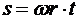 Þ
Þ 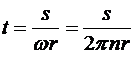 .
.
Без учета влияния силы тяжести будем искать среднюю скорость пули по формуле:
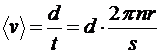 .
.
Вычислим:
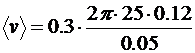 =113 (м/с)
=113 (м/с)
В вертикальном направлении пуля движется с ускорением силы тяжести, поэтому смещение пробоин в вертикальном направлении равно:
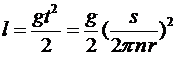 .
.
Вычислим:
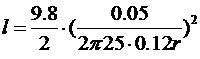 =35 (мкм)
=35 (мкм)
Ответ: 113 м/с; 35 мкм.
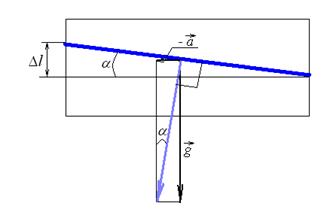
№2. Бак в тендере паровоза имеет длину l=4 м. Какова разность Dl уровней воды у переднего и заднего концов бака при движении поезда с ускорением а=0,5 м/с2? [20,4 см]
 Дано:
Дано:
l=4 м
а=0,5 м/с2
Найти: Dl - ?
Решение.
Рассматривая воду в баке относительно неинерциальной системы отсчета, связанной с ускоренно движущимся вагоном, приходим к необходимости учета силы инерции 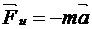 .
.
Воспользуемся принципом эквивалентности и построим на рис. векторную сумму ускорений силы тяжести и силы инерции. Поверхность воды в баке будет перпендикулярна этому вектору.
Геометрически находим искомую величину:
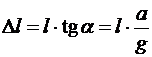 .
.
Вычислим:
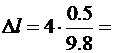 0,204 (м)= 20,4 (см).
0,204 (м)= 20,4 (см).
Ответ: 20,4 см.
Динамика материальной точки, движущейся по окружности
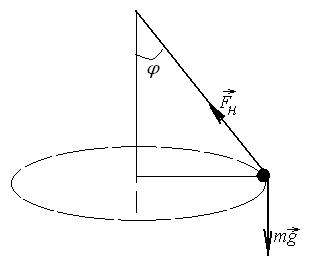 №3. Грузик, привязанный к нити длиной l=1 м, описывает окружность в горизонтальной плоскости. Определить период Т обращения, если нить отклонена на угол j=60о от вертикали. [1,42 c]
№3. Грузик, привязанный к нити длиной l=1 м, описывает окружность в горизонтальной плоскости. Определить период Т обращения, если нить отклонена на угол j=60о от вертикали. [1,42 c]
Дано:
l=1 м
j=60о
Найти: Т-?
Решение. Центростремительное ускорение сообщает грузику результирующая сил тяжести и натяжения нити, точнее горизонтальная составляющая силы натяжения нити (ее вертикальная составляющая компенсирует силу тяжести). По второму закону Ньютона:
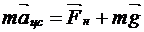 .
.
В проекциях на горизонтальную и вертикальную оси:
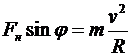 ,
,
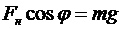 .
.
Отсюда
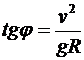 Þ
Þ 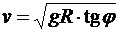
По определению периода имеем:
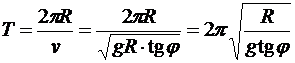 ,
, 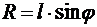
Окончательно:
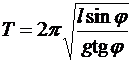 .
.
Вычислим:
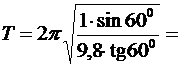 1,419 (с)»1,42 (с).
1,419 (с)»1,42 (с).
Ответ: 1,42 с.
Работа и энергия
№4. Насос выбрасывает струю воды диаметром d=2 см со скоростью v=20 м/с. Найти мощность N, необходимую для выбрасывания воды. [ 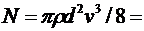 1,26 кВт, r- плотность воды]
1,26 кВт, r- плотность воды]
Дано:
d=0,02 м
v=20 м/с
Найти: N-?
Решение. По определению мощность измеряется работой, совершаемой за единицу времени. В данном случае работа идет на сообщение кинетической энергии воде. За время t объем выброшенной воды равен:
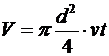 ,
,
тогда масса этой воды
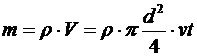 .
.
Ее кинетическая энергия
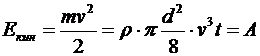 ,
,
тогда искомая мощность
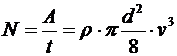 .
.
Вычислим:
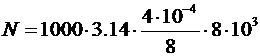 =1,26×103 (Вт)=1,26 (кВт).
=1,26×103 (Вт)=1,26 (кВт).
Ответ: 1,26 кВт.
№5.Точка совершает гармонические колебания. Наибольшее смещение хmax точки равно 10 см, наибольшая скорость  =20 см/с. Найти угловую частоту w колебаний и максимальное ускорение
=20 см/с. Найти угловую частоту w колебаний и максимальное ускорение  точки. [2 с-1; 40 см/с2]
точки. [2 с-1; 40 см/с2]
Дано:
хmax=0,1 м
 =0,2 м/с
=0,2 м/с
Найти: w,  -?
-?
Решение. Запишем уравнение гармонических колебаний:
 .
.
Тогда, дифференцируя, получим закон изменения скорости:
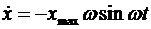 Þ
Þ 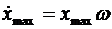 ,
,
тогда
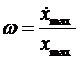 .
.
Вычислим:
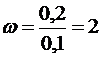 с-1.
с-1.
Снова дифференцируем:
 Þ
Þ 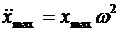 .
.
Вычислим:
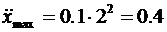 (м/с2)= 40 см/с2.
(м/с2)= 40 см/с2.
Ответ: 40 см/с2.
№6. Ареометр массой m=50 г, имеющий трубку диаметром d=1 см, плавает в воде. Ареометр немного погрузили в воду и затем предоставили самому себе, в результате чего он стал совершать гармонические колебания. Найти период Т этих колебаний. [ 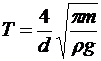 =1.6 c, r- плотность]
=1.6 c, r- плотность]
Дано:
m=0,05 г
d=0,01 м
Найти: Т-?
Решение. В состоянии равновесия сила тяжести ареометра компенсируется силой Архимеда, т.к. ареометр и здесь частично погружен в воду. При дополнительном погружении ареометра в воду на величину х (без учета статического смещения) на него начинает действовать добавочная сила, равная 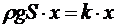 и направленная к положению равновесия. Отсюда видно, что эта сила – квазиупругая с коэффициентом
и направленная к положению равновесия. Отсюда видно, что эта сила – квазиупругая с коэффициентом
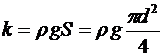 ,
,
где r - плотность воды, в которой плавает ареометр.
Тогда как для гармонического осциллятора найдем период колебаний ареометра:
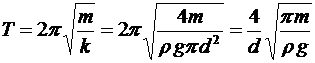 .
.
Вычислим:
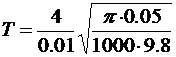 =1,601 (с).
=1,601 (с).
Ответ: 1,6 с.
№7. Велосипедист ехал из одного пункта в другой. Первую треть пути он проехал со скоростью 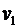 =18 км/ч. Далее половину оставшегося времени он ехал со скоростью
=18 км/ч. Далее половину оставшегося времени он ехал со скоростью 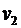 =22 км/ч, после чего до конечного пункта он шел пешком со скоростью
=22 км/ч, после чего до конечного пункта он шел пешком со скоростью 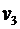 =5 км/ч. Определить среднюю скорость
=5 км/ч. Определить среднюю скорость 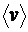 велосипедиста.
велосипедиста.
Дано: 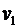 =18 км/ч=5 м/с, =18 км/ч=5 м/с, 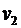 =22 км/ч= =22 км/ч= 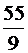 м/с, м/с, 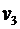 =5 км/ч= =5 км/ч= 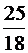 м/с. м/с. | Решение. 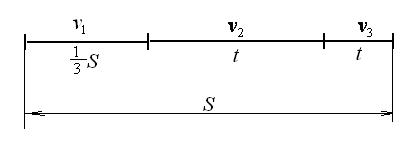 По определению: По определению: 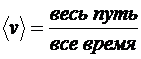 . . |
Найти: 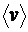 -? -? |
Получаем: 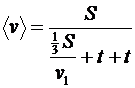 .
.
Также, сравнивая расстояния, получаем:
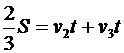 Þ
Þ 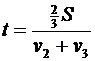 .
.
Подставляем в равенство для средней скорости:
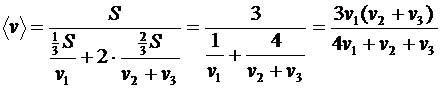 .
.
Вычисляем:
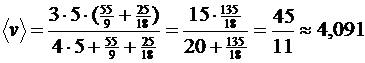 (м/с).
(м/с).
Иначе в км/ч:
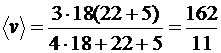 =14,727 (км/ч)
=14,727 (км/ч)
Ответ: 4,091 м/с или 14,727 км/ч.
№8. Конькобежец, стоя на коньках на льду, бросает камень массой 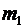 =2,5 кг под углом a=300 к горизонту со скоростью v=10 м/с. Какова будет начальная скорость
=2,5 кг под углом a=300 к горизонту со скоростью v=10 м/с. Какова будет начальная скорость 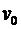 движения конькобежца, если масса его m2=60 кг? Перемещением конькобежца во время броска пренебречь.
движения конькобежца, если масса его m2=60 кг? Перемещением конькобежца во время броска пренебречь.
Дано: 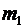 =2,5 кг, a=300, =2,5 кг, a=300, 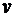 =10 м/с, =10 м/с, 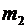 =60 кг. =60 кг. | Решение. 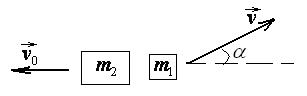 Так как время броска мало, то импульсом внешних сил, действующих на систему « Так как время броска мало, то импульсом внешних сил, действующих на систему « 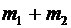 » в горизонтальном направлении (сила трения), можно пренебречь. Тогда в соответствии с законом сохранения импульса можно записать: » в горизонтальном направлении (сила трения), можно пренебречь. Тогда в соответствии с законом сохранения импульса можно записать: |
Найти: 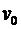 -? -? |
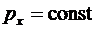 ,
,
Отсюда для состояний «до броска» и «после броска» имеем:
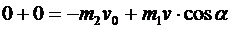 Þ
Þ 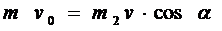
Þ 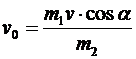 .
.
Вычислим:
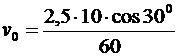 =0,361 (м/с).
=0,361 (м/с).
Ответ: 0,361 м/с.
№9. Определить КПД h неупругого удара бойка массой 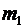 =0,5 т, падающего на сваю массой
=0,5 т, падающего на сваю массой 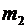 =120 кг. Полезной считать энергию, затраченную на вбивание сваи.
=120 кг. Полезной считать энергию, затраченную на вбивание сваи.
Дано: 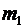 =500 кг, =500 кг, 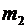 =120 кг. =120 кг. | Решение. В задаче рассмаривается неупругий удар бойка и сваи. Пусть скорость бойка непосредственно перед ударом равна v. После удара оба тела будут двигаться как одно целое с некоторой начальной скоростью u. По закону сохранения импульса найдем: |
| Найти: h - ? |
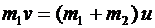 Þ
Þ 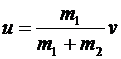 Þ
Þ 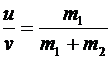 .
.
На вбивание сваи расходуется кинетическая энергия совместного движения после удара. Поэтому:
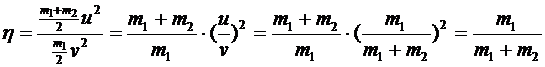 .
.
Вычислим:
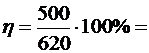 80,645»81%.
80,645»81%.
Ответ: »81%.
№10. Какую нужно совершить работу А, чтобы пружину жесткостью k=800 Н/м, сжатую на х=6 см, дополнительно сжать на Dх=8 см?
| Дано: k=800 Н/м, х=0,06 м, Dх=0,08 м. | Решение. Искомая работа будет равна приращению потенцальной энергии деформации пружины: 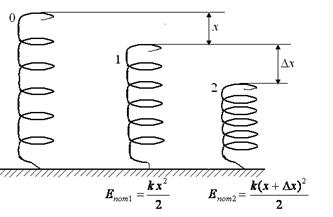 |
| Найти: А-? |
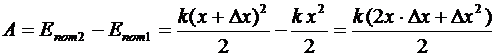 .
.
Вычислим:
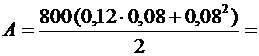 6,4 (Дж).
6,4 (Дж).
Ответ: 6,4 Дж.
№11. По круговой орбите вокруг Земли обращается спутник с периодом Т=90 мин. Определить высоту спутника. Ускорение свободного падения g у поверхности Земли и ее радиус R считать известными.
| Дано: Т=5400 с, g=9,8 м/с2, R=64×105 м. | Решение. 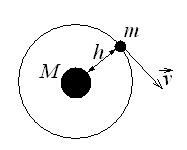 |
| Найти: h-? |
Спутник движется относительно Земли по круговой орбите, т.е. имеет центростремительное ускорение, которое ему сообщает сила тяготения. По закону всемирного тяготения:
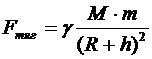 .
.
По второму закону Ньютона для спутника:
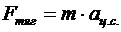 Þ
Þ
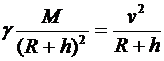 .
.
Учли выражение для центростремительного ускорения ( 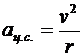 , где r - радиус окружности вращения). Получаем:
, где r - радиус окружности вращения). Получаем:
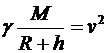 Þ
Þ 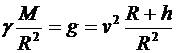 .
.
В соответствии с определениями периода вращения и скорости скорость равна:
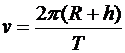 .
.
Подставляем: 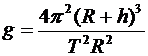 Þ
Þ 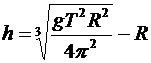 .
.
Вычислим: 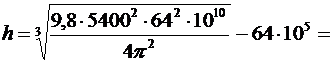 2,681×105 (м)»268 (км).
2,681×105 (м)»268 (км).
Ответ: »268 км.
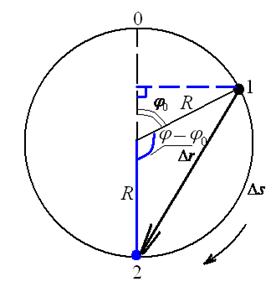
№12. Материальная точка движется по окружности с постоянной угловой скоростью 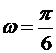 рад/с. Во сколько раз путь Ds, пройденный точкой за время t=4 с, будет больше модуля ее перемещения Dr? Принять, что в момент начала отсчета времени радиус-вектор r, задающий положение точки на окружности, относительно исходного положения был повернут на угол
рад/с. Во сколько раз путь Ds, пройденный точкой за время t=4 с, будет больше модуля ее перемещения Dr? Принять, что в момент начала отсчета времени радиус-вектор r, задающий положение точки на окружности, относительно исходного положения был повернут на угол 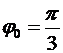 рад.
рад.
Дано: 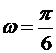 рад/с; t=4 с; рад/с; t=4 с; 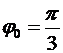 рад рад | Решение. При равномерном движении по окружности положение точки можно задать указанием угла поворота относительно некоторого начала отсчета. Тогда через время t материальная точка окажется в положении, которому соответствует угол 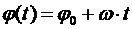 . Вычислим для t=4 с: . Вычислим для t=4 с: 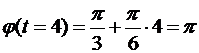 . Укажем на рис. Начальное и конечное положения точки. Далее из геометрических соображений находим искомое отношение: . Укажем на рис. Начальное и конечное положения точки. Далее из геометрических соображений находим искомое отношение: 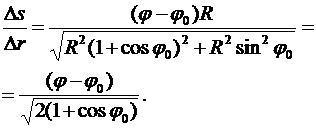 Вычислим: Вычислим: 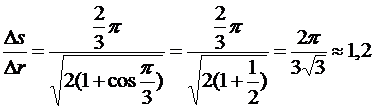 Ответ: в 1,2 раза. Ответ: в 1,2 раза. |
Найти:  -? -? | |
 |
№13. Снаряд, летевший со скоростью v=400 м/с, в верхней точке траектории разорвался на два осколка. Меньший осколок, масса которого составляет 40% от массы снаряда, полетел в противоположном направлении со скоростью u1=150 м/с. Определить скорость v2 большего осколка.
| Дано: v=400 м/с, k=0,4; u1=150 м/с | Решение. В верхней точке траектории скорость снаряда была направлена горизонтально. 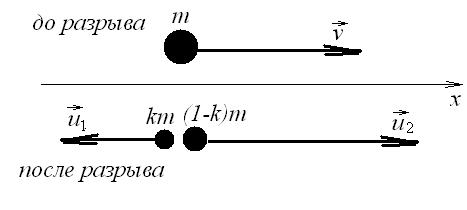 Будем искать скорость большего осколка сразу после разрыва. Тогда, считая время разрыва достаточно малым, применим закон сохранения импульса для системы «m»: Будем искать скорость большего осколка сразу после разрыва. Тогда, считая время разрыва достаточно малым, применим закон сохранения импульса для системы «m»: 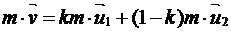 , Отсюда делаем вывод, что скорость большего снаряда направлена также по горизонтали. В проекции на горизонтальную ось х (направление движения снаряда в момент разрыва): , Отсюда делаем вывод, что скорость большего снаряда направлена также по горизонтали. В проекции на горизонтальную ось х (направление движения снаряда в момент разрыва): 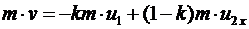 откуда выразим скорость второго осколка: откуда выразим скорость второго осколка: 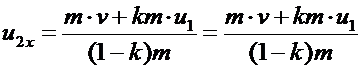 . Вычислим: . Вычислим: 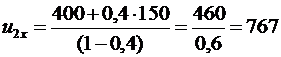 (м/с). Ответ: 767 м/с в направлении движения снаряда до разрыва. (м/с). Ответ: 767 м/с в направлении движения снаряда до разрыва. |
| Найти: u2-? |
№14. Из ствола автоматического пистолета вылетела пуля массой m1=10 г со скоростью v=300 м/с. Затвор пистолета массой m2=200 г прижимается к стволу пружиной, жесткость которой k=25 кН/м. На какое расстояние отойдет затвор после выстрела? Считать, что пистолет жестко закреплен.
| Дано: m1=10-2 кг; m2=0,2 г v=300 м/с; k=25∙103 Н/м | Решение. 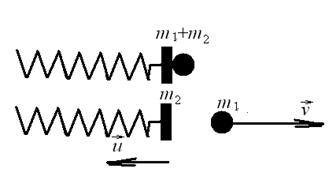 |
| Найти: Dх-? | |
К системе «затвор-пуля» можно применить закон сохранения импульса, считая время взаимодействия достаточно малым. Тогда импульсы системы до и после взаимодействия равны. Импульс до взаимодействия (до выстрела) равен нулю, тогда суммарный импульс системы после выстрела также равен нулю, или импульс пули по значению равен импульсу затвора (а их направления противоположны): 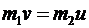 Þ Þ 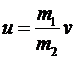 - - скорость затвора после выстрела, тогда кинетическая энергия затвора равна - - скорость затвора после выстрела, тогда кинетическая энергия затвора равна 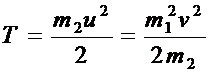 . Далее рассматриваем систему «затвор-пружина»: в ней действуют только потенциальные силы (сила упругости пружины). Влияние внешних сил (силы тяжести) не существенно. Тогда по закону сохранения энергии: . Далее рассматриваем систему «затвор-пружина»: в ней действуют только потенциальные силы (сила упругости пружины). Влияние внешних сил (силы тяжести) не существенно. Тогда по закону сохранения энергии: 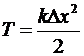 Þ Þ 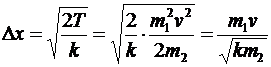 - - искомое расстояние. Проверим размерность: - - искомое расстояние. Проверим размерность: 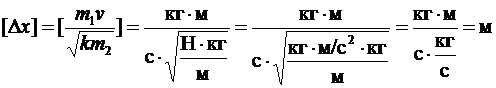 . Вычислим: . Вычислим: 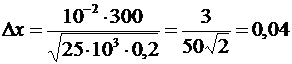 (м)=4 (см). Ответ: на 4 см. (м)=4 (см). Ответ: на 4 см. |
№15. Написать уравнение гармонического колебательного движения, если максимальное ускорение точки равно 0,493 м/с2, период колебаний 2 с и смещение точки от положения равновесия в начальный момент времени 0,025 м.
Дано: аmax=0,493 м/с2,
Т=2 с,
х0=0,025 м
Решение. Уравнение гармонического колебательного движения имеет вид:
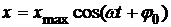 ,
,
где 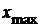 - амплитуда колебаний,
- амплитуда колебаний, 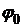 - начальная фаза, w - циклическая частота колебаний.
- начальная фаза, w - циклическая частота колебаний.
При максимальном отклонении от положения равновесия квазиупругая сила максимальна, т.е. имеет место равенство
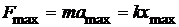 Þ
Þ 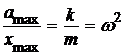 .
.
Циклическая частота связана с периодом колебаний:
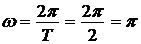 (рад/с2).
(рад/с2).
Тогда амплитуда равна
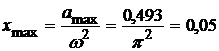 (м)
(м)
В начальный момент времени, т.е. при t=0 уравнение гармонических колебаний примет вид:
 Þ
Þ 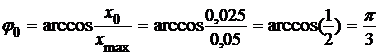 (рад).
(рад).
Получаем искомое уравнение

Ответ: 
№16. Из пружинного пистолета с пружиной жесткостью k=150 Н/м был произведен выстрел пулей массой m=8 г. Определить скорость v пули при вылете ее из пистолета, если пружина была сжата на Dх=4 см.
| Дано: k=150 Н/м; m=8∙10-3 кг; Dх=0,04 м | Решение. 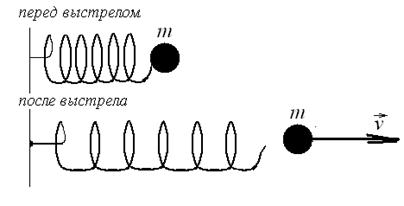 |
| Найти: v-? |
Рассмотрим систему «пружина-пуля». В ней нет непотенциальных сил, поэтому полная механическая энергия системы сохраняется. При выстреле потенциальная энергия деформации пружины переходит в кинетическую энергию пули:
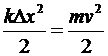 Þ
Þ 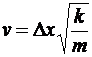 .
.
Проверка размерности аналогична предыдущей задаче.
Вычислим:
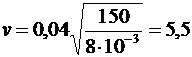 (м/с).
(м/с).
Ответ: 5,5 м/с.
№ 17. Радиус спутника Сириуса в 7 раз, а средняя плотность в 1000 раз больше радиуса и плотности Земли. Зная ускорение свободного падения у поверхности Земли, определить ускорение свободного падения у поверхности Сириуса.
| Дано: n=7 k=1000 g=9,8 м/с2 | 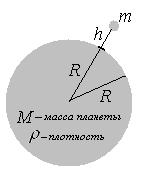 Решение. По закону всемирного тяготения тело m притягивается планетой М с силой: Решение. По закону всемирного тяготения тело m притягивается планетой М с силой: 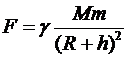 . . |
| Найти: g1 -? |
Вблизи поверхности планеты:
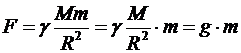 ,
,
где g – ускорение свободного падения для этой планеты.
Выразим массу планеты через объем и среднюю плотность ее вещества:
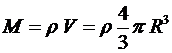 .
.
Тогда получаем
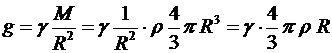 - для Земли,
- для Земли,
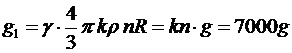 - для Сириуса.
- для Сириуса.
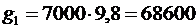 (м/с2).
(м/с2).
Ответ: 68,6 км/с2.
