Характеристики колебательной системы с затуханием
Характеристиками колебательной системы с затуханием являются: декремент затухания, равный отношению амплитуд колебаний, отличающихся на период 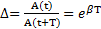 и логарифмический декремент затухания
и логарифмический декремент затухания
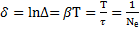 ,
,
где 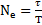 – число колебаний, которое совершает система за время затухания колебаний
– число колебаний, которое совершает система за время затухания колебаний 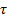 . Отсюда следует, что амплитуда затухающих колебаний может быть представлена в виде
. Отсюда следует, что амплитуда затухающих колебаний может быть представлена в виде 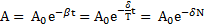 , где
, где 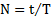 – число колебаний за время t. Декремент и логарифмический декремент затухания связаны соотношением
– число колебаний за время t. Декремент и логарифмический декремент затухания связаны соотношением 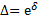 .
.
Другой характеристикой является добротность колебательной системы Q, равная отношению энергии колебаний W(t)с множителем 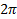 к ее потерям за период:
к ее потерям за период: 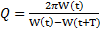 . Учитывая что,
. Учитывая что, 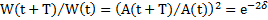 и
и 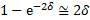 , получим
, получим
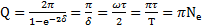 .
.
Добротность характеризует способность колебательной системы сохранять запасенную энергию. Чем она выше, тем лучше колебательная система сохраняет колебания.
Пример 1. Маятник за время 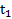 совершил N колебаний, а за время
совершил N колебаний, а за время 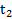 их амплитуда уменьшилась в n раз. Найти логарифмический декремент затухания и добротность колебательной системы.
их амплитуда уменьшилась в n раз. Найти логарифмический декремент затухания и добротность колебательной системы.
Дано: 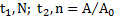 . Найти:
. Найти: 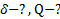
Решение:Период затухающих колебаний 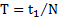 . Их амплитуда в момент времени
. Их амплитуда в момент времени 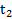 равна
равна 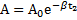 . Тогда уменьшение амплитуды за время
. Тогда уменьшение амплитуды за время 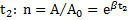 . Отсюда
. Отсюда 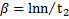 . Логарифмический декремент затухания
. Логарифмический декремент затухания 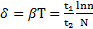 . Если
. Если 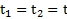 , то
, то 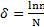 . Добротность колебательной системы
. Добротность колебательной системы 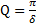 .
.
Ответ: 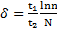 ,
, 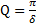 .
.
Пример 2. Колебательная система с добротностью Q за некоторое время совершила N колебаний. Во сколько раз уменьшилась амплитуда ее колебаний за это время?
Дано: 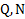 . Найти:
. Найти: 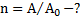
Решение: Логарифмический декремент затухания 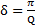 . Амплитуда затухающих колебаний с учетом
. Амплитуда затухающих колебаний с учетом 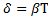 и
и 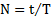 равна
равна 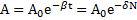 . Откуда
. Откуда 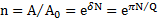 .
.
Ответ: 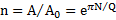 .
.
Пример 3. Математический маятник длиной l имеет логарифмический декремент затухания δ. Найти коэффициент затухания колебаний, частоту и период затухающих колебаний.
Дано: l, g, δ. Найти: 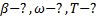
Решение: Частота собственных колебаний маятника 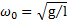 . Логарифмический декремент затухания
. Логарифмический декремент затухания 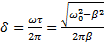 . Откуда
. Откуда 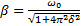 . Частота затухающих колебаний
. Частота затухающих колебаний 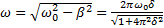 . Ответ:
. Ответ: 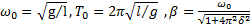 ,
, 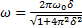 ,
, 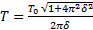 .
.
Вынужденные колебания
Если на колебательную систему действует внешняя переменная сила 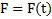 , то она совершает вынужденные колебания. Если внешняя сила периодическая:
, то она совершает вынужденные колебания. Если внешняя сила периодическая: 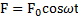 , то уравнение вынужденных колебаний в системе с линейной силой трения имеет вид
, то уравнение вынужденных колебаний в системе с линейной силой трения имеет вид
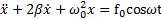 , где
, где 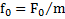 . Решением этого уравнения в режиме установившихся колебаний (рис.75), происходящих с частотой ω вынуждающей силы, является функция
. Решением этого уравнения в режиме установившихся колебаний (рис.75), происходящих с частотой ω вынуждающей силы, является функция
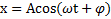 , где
, где 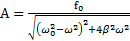 ,
, 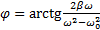 .
.
Рис.75
Рис.77
График зависимости амплитуды колебаний 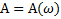 от частоты
от частоты 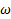 вынуждающей силы называется амплитудно-частотной характеристикой (АЧХ) колебательной системы или резонансной кривой (рис.77). Амплитуда вынужденных колебаний имеет максимальное значение
вынуждающей силы называется амплитудно-частотной характеристикой (АЧХ) колебательной системы или резонансной кривой (рис.77). Амплитуда вынужденных колебаний имеет максимальное значение 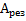 при частоте
при частоте 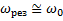 , близкой к собственной частоте
, близкой к собственной частоте 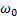 колебаний системы, называемыми амплитудой резонанса и резонансной частотой, равными
колебаний системы, называемыми амплитудой резонанса и резонансной частотой, равными
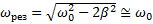 ,
, 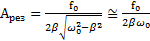 .
.
Частота 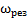 находится из условия минимума подкоренной функции
находится из условия минимума подкоренной функции 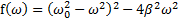 в зависимости
в зависимости 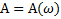 .
.
Если на графике АЧХ провести на уровне 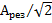 прямую, параллельную оси частот, то она пересечет резонансную кривую в точках
прямую, параллельную оси частот, то она пересечет резонансную кривую в точках 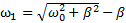 и
и 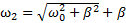 , являющихся решением уравнения
, являющихся решением уравнения 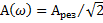 . Расстояние между этими точками
. Расстояние между этими точками 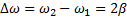 называют шириной резонансной кривой (рис.77).
называют шириной резонансной кривой (рис.77).
Рис.77
Если параметры 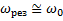 и
и 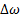 (или
(или 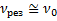 и
и 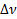 ) определены по АЧХ колебательной системы, то можно определить ее добротность
) определены по АЧХ колебательной системы, то можно определить ее добротность
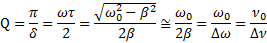
В опыте можно строить как АЧХ колебательной системы 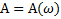 , так и зависимость
, так и зависимость 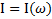 , где
, где 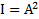 – интенсивность колебаний, которая характеризует поглощение энергии колебаний колебательной системой, возбуждаемых внешней силой. С учетом
– интенсивность колебаний, которая характеризует поглощение энергии колебаний колебательной системой, возбуждаемых внешней силой. С учетом 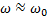 и
и 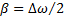 эти зависимости имеют вид
эти зависимости имеют вид
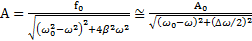 ,
, 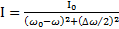 ,
,
где 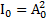 ,
, 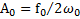 . Полученная зависимость
. Полученная зависимость 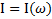 называется функцией Лоренца.
называется функцией Лоренца.
Пример 1. В опыте по АЧХ колебательной системы 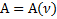 определена ее резонансная частота
определена ее резонансная частота 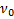 и ширина
и ширина 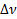 (Гц) на уровне
(Гц) на уровне 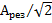 . Найти время затухания колебаний, возбуждаемых в системе периодической силой, логарифмический декремент затухания и добротность колебательной системы.
. Найти время затухания колебаний, возбуждаемых в системе периодической силой, логарифмический декремент затухания и добротность колебательной системы.
Дано: 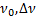 (Гц). Найти:
(Гц). Найти: 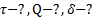
Решение: Если колебания возбуждаются периодической силой, то ширина резонансной кривой на уровне 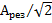 равна
равна 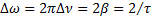 . Откуда время затухания возбуждаемых колебаний равно
. Откуда время затухания возбуждаемых колебаний равно 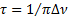 . Ответ:
. Ответ: 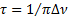 ,
, 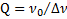 ,
, 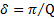 .
.
