Момент инерции материальной точки и тела. Теорема Штейнера.
При вращении материальной точки массой m вокруг фиксированной оси Z по окружности радиуса r, лежащей в плоскости, перпендикулярной оси Z, со скоростью v момент импульса равен 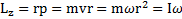 . Величину
. Величину 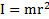 называют моментом инерции материальной точки относительно оси Z.
называют моментом инерции материальной точки относительно оси Z.
Если вокруг фиксированной оси вращается твердое тело, то его можно разбить на совокупность материальных точек с моментами инерции 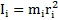 , вращающихся вокруг оси с одинаковой угловой скоростью
, вращающихся вокруг оси с одинаковой угловой скоростью 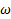 и имеющих моменты импульса
и имеющих моменты импульса 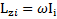 . Тогда момент импульса твердого тела относительно оси вращения будет равен
. Тогда момент импульса твердого тела относительно оси вращения будет равен 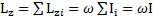 , где величину
, где величину 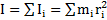 называют моментом инерции твердого тела относительно выбранной оси вращения.
называют моментом инерции твердого тела относительно выбранной оси вращения.
Однако вычислить момент инерции твердого тела по этой формуле нельзя. Для тела с распределенной массой его вычисляют по формуле 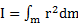 . Для сведения этого интеграла к математическому элемент массы
. Для сведения этого интеграла к математическому элемент массы 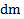 тела в зависимости от характера ее распределения (по кривой, поверхности или объему тела) представляют в виде
тела в зависимости от характера ее распределения (по кривой, поверхности или объему тела) представляют в виде 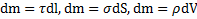 , где
, где 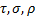 – линейная, поверхностная и объемная плотности тела, соответственно.
– линейная, поверхностная и объемная плотности тела, соответственно.
В справочниках приводятся только моменты инерции 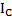 тел относительно осей вращения, проходящих через их центр масс (ЦМ)C. Так, момент инерции стержня длиной l и массой m относительно оси вращения, перпендикулярной стержню и проходящей через его ЦМ, равен
тел относительно осей вращения, проходящих через их центр масс (ЦМ)C. Так, момент инерции стержня длиной l и массой m относительно оси вращения, перпендикулярной стержню и проходящей через его ЦМ, равен 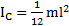 . Момент инерции круглых тел массой m и радиусом R относительно оси вращения, проходящей через их ЦМ вдоль оси их симметрии –
. Момент инерции круглых тел массой m и радиусом R относительно оси вращения, проходящей через их ЦМ вдоль оси их симметрии – 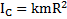 , где k – коэффициент инерции равный k = 1 для обруча и полого цилиндра,
, где k – коэффициент инерции равный k = 1 для обруча и полого цилиндра, 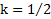 для диска и сплошного цилиндра,
для диска и сплошного цилиндра, 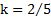 для шара,
для шара, 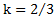 для сферы.
для сферы.
Для кольца или цилиндра с внутренним и внешним радиусами 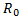 и
и 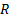 –
– 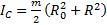 или
или 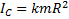 , где
, где 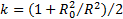 . В частных случаях обруча и полого цилиндра
. В частных случаях обруча и полого цилиндра 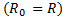 , диска и сплошного цилиндра
, диска и сплошного цилиндра 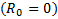 опять придем к прежним формулам моментов инерции этих тел.
опять придем к прежним формулам моментов инерции этих тел.
Для сферы с толстыми стенками с внутренним и внешними радиусами стенок 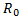 и
и 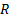 –
– 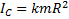 , где
, где 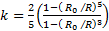 .
.
Если ось вращения тела смещена от оси вращения, проходящей через его ЦМ, на расстояниеa и параллельна ей, то момент инерции тела относительно этой оси рассчитывают по теореме Штейнера: 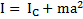 , где m – масса тела. Например, момент инерции круглых тел относительно оси вращения, касающейся их поверхности (a = R) и параллельной исходной оси вращения, проходящей через ЦМ тела, по теореме Штейнера равен
, где m – масса тела. Например, момент инерции круглых тел относительно оси вращения, касающейся их поверхности (a = R) и параллельной исходной оси вращения, проходящей через ЦМ тела, по теореме Штейнера равен 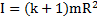 .
.
Пример 1. Перпендикулярно к боковой поверхности прямого цилиндра массой 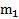 и радиусом
и радиусом 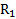 прикреплен стержень массой
прикреплен стержень массой 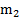 и длиной l. Ко второму концу стержня прикреплен шар массой
и длиной l. Ко второму концу стержня прикреплен шар массой 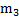 и радиусом
и радиусом 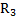 (рис.51). Найти момент инерции этой системы тел относительно оси цилиндра.
(рис.51). Найти момент инерции этой системы тел относительно оси цилиндра.
Рис.51
Дано: 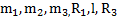 . Найти:
. Найти: 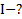
Решение: Решение задачи построим в виде последовательного алгоритма. Расстояния ЦМ тел до оси цилиндра: 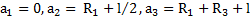 . Моменты инерции тел относительно их ЦМ:
. Моменты инерции тел относительно их ЦМ: 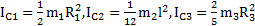 . Моменты инерции тел относительно оси цилиндра, рассчитанные по теореме Штейнера:
. Моменты инерции тел относительно оси цилиндра, рассчитанные по теореме Штейнера: 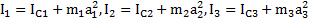 . Полный момент инерции системы тел:
. Полный момент инерции системы тел: 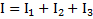 .
.
Ответ: 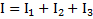 .
.
Пример 2. Найти момент инерции каркаса равностороннего треугольника массой m со сторонами длиной l относительно оси вращения, проходящую через его ЦМ, перпендикулярную его плоскости (рис.52). Каким станет момент инерции треугольника, если ось вращения параллельно перенести в одну из его вершин.
Рис.52
Дано: m, l. Найти: 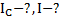
Решение: ЦМ С равностороннего треугольника находится в точке пересечения его высот. Масса одной стороны треугольника 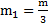 , расстояния от ЦМ сторон треугольника до оси вращения
, расстояния от ЦМ сторон треугольника до оси вращения 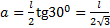 . Момент инерции одной стороны треугольника относительно оси вращения по теореме Штейнера:
. Момент инерции одной стороны треугольника относительно оси вращения по теореме Штейнера: 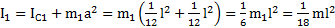 . Момент инерции треугольника
. Момент инерции треугольника 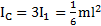 .
.
При параллельном переносе оси вращения в одну из вершин треугольника расстояние между ЦМ треугольника и новой осью вращения станет равным 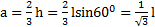 , а его новый момент инерции по теореме Штейнера –
, а его новый момент инерции по теореме Штейнера – 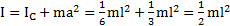 .
.
Ответ: 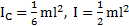 .
.
Пример 3. Найти момент инерции каркаса квадрата массой m со сторонами длиной l относительно оси вращения, проходящей через его центр и перпендикулярной плоскости квадрата (рис.53).
Рис. 53
Дано: 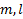 . Найти
. Найти 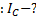
Решение: Масса одной стороны квадрата 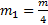 , расстояния от оси вращения до сторон квадрата
, расстояния от оси вращения до сторон квадрата 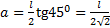 . Момент инерции одной стороны квадрата относительно выбранной оси вращения по теореме Штейнера:
. Момент инерции одной стороны квадрата относительно выбранной оси вращения по теореме Штейнера: 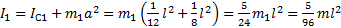 . Момент инерции квадрата
. Момент инерции квадрата 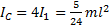 .
.
Ответ: 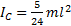 .
.
Пример 4. Найти момент инерции стержня длиной l и массой m, наклоненного под углом α к оси вращения, проходящей через его ЦМ.
Рис.54
Дано: m, l, α.Найти: 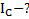
Решение: Для вычисления момента инерции выберем систему координат как это показано на рис.54. Возьмем на оси стержня с линейной плотностью массы 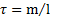 элемент массы
элемент массы 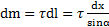 и моментом инерции
и моментом инерции 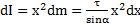 . Тогда момент инерции стержня относительно оси вращения, проходящей через его ЦМ
. Тогда момент инерции стержня относительно оси вращения, проходящей через его ЦМ
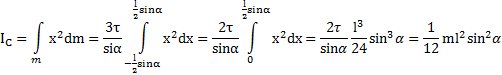
Из полученного выражения следует, что вклад в момент инерции стержня дает его проекция 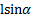 на направление, перпендикулярное оси вращения.
на направление, перпендикулярное оси вращения.
Ответ: 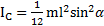 .
.
Пример 5. Найти момент инерции стержня длиной l и массой m, наклоненного под углом α к оси вращения, ближайший конец которого отстоит от оси вращения на расстояние a (рис.55). Ось вращения и стержень лежат в одной плоскости.
Рис.55
Дано: 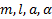 . Найти:
. Найти: 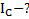
Решение: Для вычисления момента инерции выберем систему координат, как это показано на рис.56. Повторяя рассуждения примера 1 и изменяя пределы интегрирования, получим для момента инерции стержня
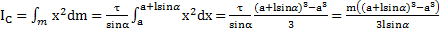 .
.
При a=0 получим 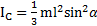 . Откуда при
. Откуда при 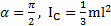 . Выражение для
. Выражение для 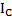 можно записать в виде
можно записать в виде
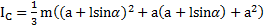 .
.
Откуда при 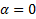 получим
получим 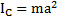 . Отсюда следует, что стержень, параллельный оси вращения, ведет себя как материальная точка.
. Отсюда следует, что стержень, параллельный оси вращения, ведет себя как материальная точка.
Пример 6. Найти момент инерции каркаса прямоугольника массой m со сторонами, равными a и b, относительно оси вращения, проходящей в его плоскости через его ЦМ параллельно стороне a (рис.56).
Рис.56
Дано: m, a, b. Найти: 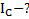
Решение: Линейная плотность массы каркаса прямоугольника равна 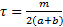 . Массы сторон длиной a и b равны соответственно
. Массы сторон длиной a и b равны соответственно 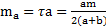 и
и 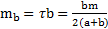 .
.
Стороны прямоугольника с длиной равной a, параллельные оси вращения, ведут себя как материальные точки с моментом инерции 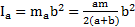 , а стороны длиной b, перпендикулярные оси вращения, как стержни с моментом инерции
, а стороны длиной b, перпендикулярные оси вращения, как стержни с моментом инерции 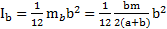 .
.
Полный момент инерции каркаса прямоугольника 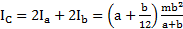 .
.
Ответ: 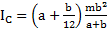 .
.
Пример 7. Вывести формулу для момента инерции прямоугольника массой m со сторонами a и b относительно оси вращения, проходящей через его ЦМ, перпендикулярно его плоскости (рис.57).
Рис.57
Дано: m, a, b. Найти: 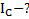
Решение: Выберем систему координат XYZ с началом О в ЦМ прямоугольника, ось Z которой перпендикулярна его плоскости. Оси X и Y направим перпендикулярно его сторонам a и b. Масса прямоугольника 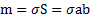 , где
, где 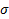 – поверхностная плотность его массы.
– поверхностная плотность его массы.
В качестве элемента поверхности возьмем прямоугольник с координатами 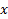 и
и 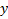 ,со сторонами
,со сторонами 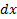 и
и 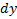 и площадью
и площадью 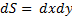 , находящийся на расстоянии
, находящийся на расстоянии 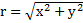 от начала О системы координат. Масса этого прямоугольника
от начала О системы координат. Масса этого прямоугольника 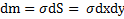 , а момент инерции
, а момент инерции 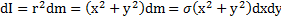 .
.
Полный момент инерции прямоугольника
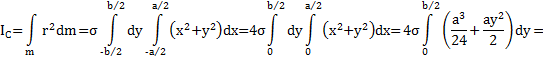
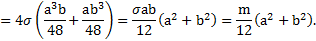
Если 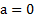 или
или 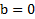 , то придем к формуле момента инерции стержня относительно оси вращения, перпендикулярной стержню и проходящей через его ЦМ.
, то придем к формуле момента инерции стержня относительно оси вращения, перпендикулярной стержню и проходящей через его ЦМ.
Ответ: 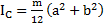 .
.
Пример 8. Вывести формулу для момента инерции равнобедренного треугольника массой m, высотой h и длиной основания, равной a, относительно оси вращения, лежащей в плоскости треугольника и проходящей вдоль его высоты.
Рис.58
Дано: m, a. Найти: 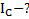
Решение: Выберем систему координат с началом О в вершине треугольника. Ось Z направим вдоль высоты треугольника к его основанию (рис.58). Масса треугольника 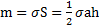 .
.
В качестве элементарного тела выберем стержень, перпендикулярный к оси Z на расстоянии z от начала О шириной dz. Из подобия треугольников длина стержня 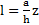 , его площадь
, его площадь 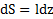 , масса
, масса 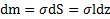 , а момент инерции
, а момент инерции 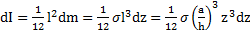 .
.
Момент инерции треугольника относительно оси вращения, проходящей вдоль его высоты
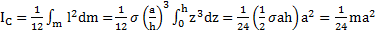 .
.
Ответ: 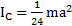 .
.
Пример 9. Вывести формулу для момента инерции равнобедренного треугольника массой m, высотой h и длиной основания, равной a, относительно оси вращения, перпендикулярной плоскости треугольника и проходящей через его вершину.
Дано: m, a,h. Найти: 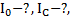
Решение: Выберем систему координат так же, как в примере 8 (рис.59). Масса треугольника 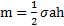 .
.
В качестве элементарного тела выберем стержень, перпендикулярный к оси X на расстоянии z от начала О шириной dz и длиной 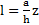 , его масса
, его масса 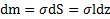 и момент инерции относительно его ЦМ
и момент инерции относительно его ЦМ 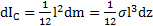 . Момент инерции стержня относительно его вершины по теореме Штейнера
. Момент инерции стержня относительно его вершины по теореме Штейнера
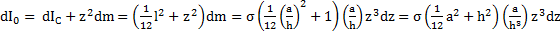 .
.
Полный момент инерции равнобедренного треугольника относительно оси вращения, проходящей через его вершину перпендикулярно его плоскости
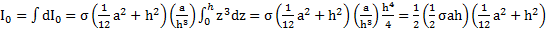 .
.
Откуда 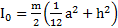 . Для равностороннего треугольника
. Для равностороннего треугольника 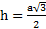 ,
, 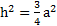 и
и 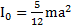 .
.
Ответ: 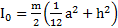 ,для равностороннего треугольника–
,для равностороннего треугольника– 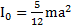 .
.
Пример 10. Вывести формулу для момента инерции равнобедренного треугольника массой m, высотой h и длиной основания, равной a, относительно оси вращения, перпендикулярной плоскости треугольника и проходящей через его ЦМ.
Дано: m, a,h. Найти: 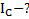
Решение: Согласно разделу Центр масс ЦМ треугольника находится от вершины треугольника на расстоянии 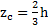 . Тогда по теореме Штейнера с учетом примера 9получим
. Тогда по теореме Штейнера с учетом примера 9получим
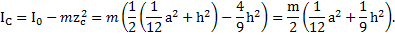
Для равностороннего треугольника 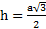 ,
, 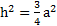 ,
, 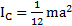 .
.
Ответ: 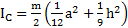 , для равностороннего треугольника –
, для равностороннего треугольника – 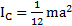 .
.
Пример 11. Вывести формулу для момента инерции кольца (полого цилиндра) массой m с внутренним и внешним радиусами 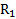 и
и 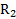 относительно оси вращения, проходящей через центр кольца, перпендикулярно его плоскости (рис.59).
относительно оси вращения, проходящей через центр кольца, перпендикулярно его плоскости (рис.59).
Рис.59
Решение: Масса кольца 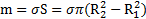 , где
, где 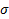 – поверхностная плотность его массы. Выберем в качестве элементарного тела кольцо радиуса r и шириной dr, площадь которого
– поверхностная плотность его массы. Выберем в качестве элементарного тела кольцо радиуса r и шириной dr, площадь которого 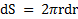 , а масса равна
, а масса равна 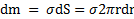 . Момент инерции кольца
. Момент инерции кольца 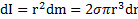 . Тогда момент инерции большого кольца
. Тогда момент инерции большого кольца
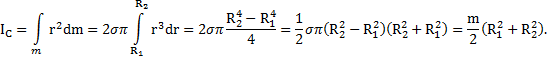
Ответ: 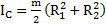 .
.
Пример 12.Вывести формулу для момента инерции кругового сектора диска массой m радиусом R относительно оси вращения, перпендикулярной его плоскости и проходящей через его вершину (рис.21, раздел 7).
Дано: m, R. Найти: 
Решение:Задачу будем решать в полярной системе координат. Начало О системы координат выберем в центре кругового сектора. Масса сектора с углом 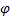 при его вершине
при его вершине 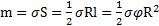 .
.
В качестве элемента массы dm выберем площадку, находящуюся на расстоянии r от точки О под углом α к оси X, перпендикулярной оси симметрии сектора. Ее площадь 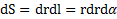 , а масса
, а масса 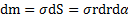 . Момент инерции кругового сектора, боковые стороны которого составляют углы
. Момент инерции кругового сектора, боковые стороны которого составляют углы 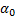 с осью X
с осью X 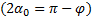 , равен
, равен
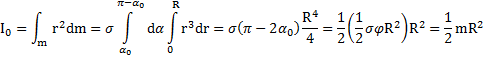
Ответ: 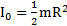 .
.
Пример 13. Вывести формулу для момента инерции для половины диска массой m и радиусом R относительно оси вращения, перпендикулярной его плоскости и проходящей через его ЦМ.
Дано: m, R. Найти: 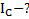
Решение: Положение ЦМ половины диска было найдено в разделе 7 – Центр масс и равно 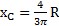 , а его момент инерции
, а его момент инерции 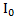 относительно его центра в О получен примере 12. Тогда момент инерции половины диска относительно его ЦМ по теореме Штейнера будет равен
относительно его центра в О получен примере 12. Тогда момент инерции половины диска относительно его ЦМ по теореме Штейнера будет равен
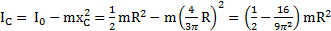 .
.
Ответ: 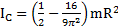 .
.
Пример 14. Вывести формулу для момента инерции диска массой m и радиусом R относительно оси вращения, лежащей в его плоскости и проходящей через его диаметр.
Рис.60
Дано: m, R. Найти: 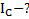
Решение: Начало О системы координат возьмем в ЦМ диска, а его ось вращения Z направим по его диаметру (рис.60). Масса диска 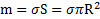 ,где
,где 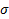 – поверхностная плотность массы диска.
– поверхностная плотность массы диска.
Для расчета момента инерции диска выберем в качестве элементарного тела стержень, перпендикулярный оси вращения Z, находящийся на расстоянии z от точки О. Длина стержня 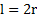 ,
, 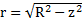 , его ширина dz, масса стержня
, его ширина dz, масса стержня 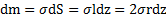 .
.
Элементарный момент инерции стержня 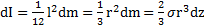 . Тогда с учетом, что при
. Тогда с учетом, что при 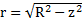 –
– 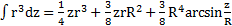 , откуда
, откуда 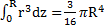 получим для полного момента инерции диска относительно оси вращения, проходящей через его диаметр
получим для полного момента инерции диска относительно оси вращения, проходящей через его диаметр
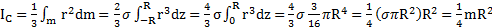 .
.
Ответ: 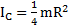 .
.
Пример 15. Вывести формулу для момента инерции кругового сектора массой m и радиусом R и углом 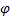 при его вершине относительно оси вращения, лежащей в его плоскости и проходящей через его ось симметрии.
при его вершине относительно оси вращения, лежащей в его плоскости и проходящей через его ось симметрии.
Дано: 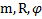 . Найти:
. Найти: 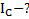
Решение:Начало О системы координат возьмем в центре кругового сектора, а его ось вращения Z направим вдоль его оси симметрии. Масса сектора 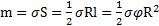 ,где
,где 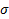 – поверхностная плотность его массы.
– поверхностная плотность его массы.
Задачу будем решать в полярной системе координат. Начало О системы координат выберем в центре кругового сектора. В качестве элемента массы dmвыберем площадку, находящуюся на расстоянии rот точки О под углом α к оси X, перпендикулярной оси Z симметрии сектора (рис.21 раздела 7). Ее координата по оси Z равна 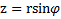 , площадь
, площадь 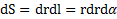 , а масса
, а масса 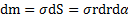 . Момент инерции кругового сектора относительно оси Z, боковые стороны которого составляют углы
. Момент инерции кругового сектора относительно оси Z, боковые стороны которого составляют углы 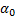 с осью X, с учетом, что
с осью X, с учетом, что 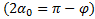
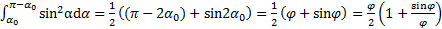 ,
,
равен
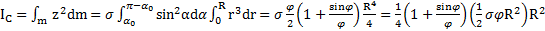 .
.
Откуда 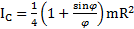 . При
. При 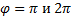 придем к моменту инерции диска и половины диска, полученному в предыдущем примере.
придем к моменту инерции диска и половины диска, полученному в предыдущем примере.
Ответ: 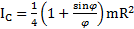 .
.
Пример 16. Вывести формулу для момента инерции шара массой m и радиусом R относительно оси вращения, проходящей через его ЦМ (рис.60).
Дано: m, R. Найти: 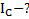
Решение: Масса шара 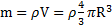 , где
, где 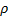 – объемная плотность массы шара.
– объемная плотность массы шара.
Выберем в качестве элементарного тела диск, лежащий в плоскости, перпендикулярной оси вращения, и отстоящий на расстояние z от ЦМ сферы. Радиус диска 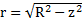 , его высота dz, а объем
, его высота dz, а объем 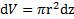 . Масса диска
. Масса диска 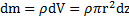 , его момент инерции
, его момент инерции 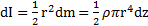 .
.
Полный момент инерции шара
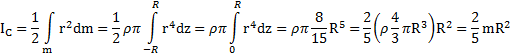
Ответ: 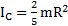 .
.
Пример 17. Вывести формулу для момента инерции шарового слоя массой m с внутренним и внешним радиусами, равными 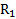 и
и 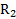 относительно оси вращения, проходящей через его ЦМ. Рассмотреть момент инерции сферы массой m и радиусом R как частный случай.
относительно оси вращения, проходящей через его ЦМ. Рассмотреть момент инерции сферы массой m и радиусом R как частный случай.
Дано: 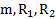 . Найти:
. Найти: 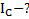
Решение: Масса шара с объемной плотностью массы ρравна 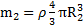 , а масса полости в нем
, а масса полости в нем 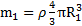 . Тогда масса шарового слоя
. Тогда масса шарового слоя 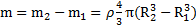 . Откуда
. Откуда 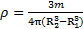 . Если момент инерции шара равен
. Если момент инерции шара равен 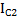 , а шаровой полости в нем
, а шаровой полости в нем 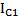 , то момент инерции шарового слоя согласно примеру 16
, то момент инерции шарового слоя согласно примеру 16 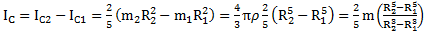 . Откуда при
. Откуда при 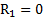 и
и 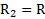 опять придем к формуле момента инерции шара
опять придем к формуле момента инерции шара 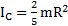 .
.
Используя преобразование 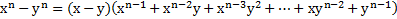 , момент инерции шарового слоя можно представить в виде
, момент инерции шарового слоя можно представить в виде
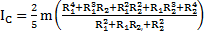 .
.
Откуда при 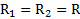 получим момент инерции сферы
получим момент инерции сферы 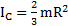 .
.
Ответ: для шарового слоя 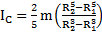 , для сферы
, для сферы 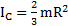 .
.
Пример 18. Вывести формулу для момента инерции прямого конуса массой m с радиусом
основания R и высотой h относительно оси вращения, проходящей через его ось симметрии.
Рис.61
Дано: m, R. Найти: 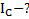
Решение: Выберем ось Z по направлению оси симметрии конуса с началом О в его вершине (рис.61). Масса конуса 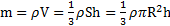 .
.
Выберем в качестве элементарного тела диск, лежащий в плоскости, перпендикулярной оси вращения и отстоящий на расстояние z от вершины конуса. Из подобия треугольников 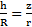 , тогда радиус диска
, тогда радиус диска 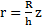 , его высота dz, а объем
, его высота dz, а объем 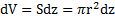 . Масса диска
. Масса диска 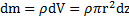 , его момент инерции
, его момент инерции 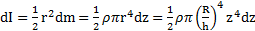 .
.
Полный момент инерции конуса
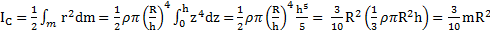 .
.
Ответ: 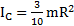 .
.
