Архимедова или выталкивающая сила

,

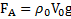где 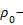плотность жидкости (газа), 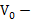объем жидкости, вытесненный телом (часть объема тела, находящаяся в жидкости), g – ускорение свободного падения. Условие равновесия тела массой m=ρV, где ρ и V – его плотность и объем, плавающего в жидкости: 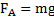или

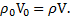
В ускоренно движущейся с ускорением aвверх или вниз системе отсчета жидкость оказывается в новом гравитационном поле с ускорением свободного падения 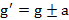, и действующая на тело сила Архимеда станет равной 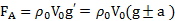. В состоянии невесомости, при свободном падении системы отсчета 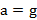, и выталкивающая сила, действующая на тело .

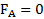5. Сила сопротивления движению тела в жидкости или газе.

При малых скоростях движения тела она вычисляется по формуле Стокса 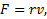где v – скорость тела, r – коэффициент лобового сопротивления. Для шара 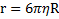, где R – радиус шара, 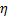– (динамическая) вязкость жидкости или газа. Движение слоев жидкости в этом случае является ламинарным, без завихрений и перемешивания слоев жидкости при движении тела в ней.

При больших скоростях движения тела силу сопротивления его движению вычисляют по формуле Ньютона 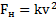. Движение слоев жидкости в этом случае является турбулентным, с завихрениями и перемешиванием ее разных слоев.

Является ли движение слоев жидкости, имеющей плотность 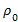и динамическую вязкость 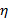, при движении шара радиуса R со скоростью v в ней ламинарным или турбулентным определяют по числу Рейнольдса 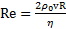. Если Re< 2300 (при течении жидкости по трубе) и Re< 150 (при падении шарика в жидкости), то движение жидкости ламинарное, в противном случае – турбулентное.

6. Сила вязкого или внутреннего трения.Эта сила возникает, между слоями вязкой среды

(жидкости или газа), движущимися относительно друг друга с разными скоростями. При ламинарном (без перемешивания слоев) течении жидкости сила вязкого трения

,

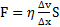где 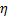– коэффициент пропорциональности, называемый динамической вязкостью жидкости или газа, 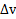– относительная скорость слоев, находящихся на расстоянии 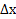друг от друга, 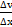– градиент скорости движущихся слоев среды в направлении X, перпендикулярном направлению векторов скорости их движения, 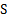– площадь их соприкосновения. В гидродинамике используется также величина 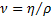, где ρ – плотность жидкости, называемая кинематической вязкостью, и величина 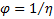, называемая текучестью.

7. Упругая и квазиупругая силы. Силы вида 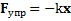или в скалярной форме ,

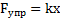где x– абсолютная (полная) деформация тела или пружины, k – упругость или коэффициент упругости, называются упругими.

Если тело массой m подвесить на пружине, то она растянется на величину 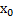, определяемую условием равновесия тела 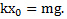Если на тело дополнительно подействовать силой F, то пружина дополнительно растянется на величину x, и полная деформация пружины станет равной 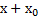. Новое условие равновесия тела примет вид 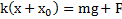, откуда 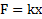. Формула вычисления этой силы похожа на формулу 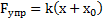упругой силы, поэтому силы вида 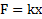называют квазиупругими.

В рассматриваемом примере сила F является равнодействующей упругой силы и силы тяжести

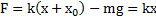
и представляет собой часть полной упругой силы. В случае колебания тела на пружине оно осуществляется только под действием квазиупругой силы (равнодействующей упругой силы и силы тяжести).

Пример 1.Найти ускорение свободного падения на расстоянии 100 км, 500 км и 1000 км от поверхности Земли. Радиус Земли 6370 км.

Дано: .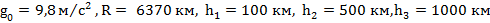

Найти: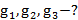

Решение: Ускорение свободного падения рассчитывается по формуле 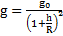, при расчете по которой получим Ответ: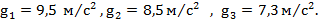

Пример 2. Тело плавает в воде, наполовину по объему погруженным в нее. Найти плотность материала тела.

Дано: 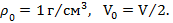Найти: ρ - ?

Решение: Согласно условию равновесия тела в жидкости 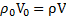плотность тела равна 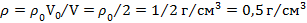. Ответ: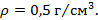

Пример 3: Льдина, имеющая форму параллелепипеда, плавает в воде, выступая из нее на 10 см. Найти толщину льдины. На какую высоту погрузится льдина, если на нее станет человек массой 80 кг? Площадь верхней поверхности льдины 8 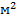. Плотности воды и льда равны 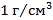и 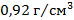,соответственно.

Дано: 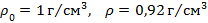, , 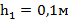M= 80 кг, 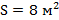. Найти: H– ?,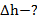

Решение: Обозначим:S –площадь сечения льдины, H – ее толщину,h – высоту льдины над водой, 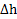– разность высот льдины над водой, Mи m – массы человека и льдины. Условия равновесия льдины в воде без человека и с человеком на ней имеют вид: 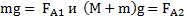, а разность этих уравнений – M 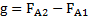. Первое уравнение приводится к виду 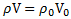или 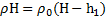, а третье – 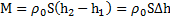.Откуда

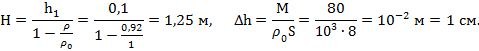
Ответ: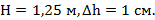

Пример 4. Свинцовый шарик с радиусом R, массой m и плотностью ρ, опущенный в жидкость плотностью 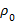, начинает падать в ней с постоянной скоростьюv. Определить вязкость жидкости .

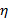Дано: 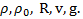Найти: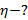

Решение: При движении с постоянной скоростью v=const ускорение шарика a= 0, и второй закон Ньютона, описывающий его движение, имеет вид 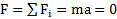. На шарик действуют: сила тяжести 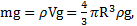архимедова сила 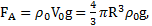сила сопротивления его движению (сила Стокса) 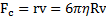. С учетом выражений этих сил второй закон Ньютона для движения шарика в жидкости примет вид (рис.22)

Рис.22

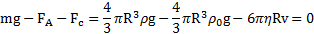
Откуда, сокращая на 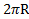, получим

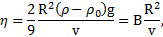
где 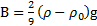– константа эксперимента. Однако это выражение неудобно для применения на практике для определения вязкости жидкости 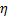из-за трудности точного экспериментального определения радиуса шарика R с помощью простейших измерительных приборов: штангенциркуля и микрометра.

Пример 5. Представить выражение для вязкости жидкости 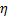, полученное в примере 4, через массу шарика m.

Дано: 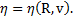Найти: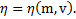

Решение: масса шарика равна 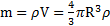, откуда радиус шарика R, выраженный через его массу 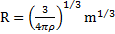. Подставляя это выражение в формулу вязкости жидкости, получим

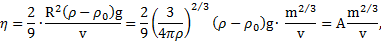
где 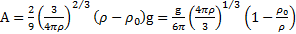– константа эксперимента.

Пример 6. Цилиндр радиуса r находится внутри коаксиального тонкостенного цилиндра радиуса R, 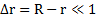. Длины цилиндров одинаковы и равны l. Между цилиндрами находится среда с вязкостью η. Внешний цилиндр приводят в движение с угловой скоростью ω. Найти силу вязкого трения, действующую на внутренний и внешний цилиндры со стороны вязкой среды.

Дано: 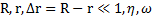. Найти: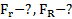

Решение: Скорость точек среды вблизи внутреннего покоящегося цилиндра 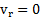, а вблизи тонкостенного вращающегося цилиндра – 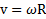. Градиент скорости слоев среды между цилиндрами в радиальном направлении 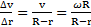. Площадь поверхности внутреннего цилиндра 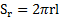. Тогда на внутренний цилиндр подействует сила вязкого трения

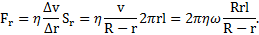
Площадь поверхности внешнего цилиндра равна 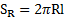и на него действует сила вязкого трения

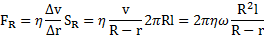
При .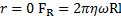

Ответ: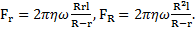

9. Законы Ньютона

Первый закон Ньютона.Существуют такие системы отсчета (СО), в которых при отсутствии внешних воздействий тело движется равномерно и прямолинейно, то есть по инерции. Такие СО называются инерциальными (ИСО).

Существует бесчисленное число ИСО, движущихся относительно друг друга равномерно и прямолинейно и достаточно найти одну из них. Примером ИСО является гелиоцентрическая система отсчета, связанная с Солнцем. Землю, вращающуюся вокруг Солнца и собственной оси, можно считать ИСО лишь в узком круге задач.

Любая ускоренно движущаяся относительно произвольной ИСО система отсчета называется неинерциальной (НИСО).

Второй закон Ньютона. В произвольной ИСО тело движется по закону

,

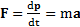где 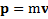– импульс тела, являющийся векторной мерой движения тела (скалярной мерой движения тела является его кинетическая энергия 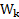), 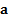– его ускорение, 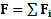– результирующая или равнодействующая сила, действующая на тело.

При решении задач на второй закон Ньютона во избежание ошибок в знаках проекций векторов сил, действующих на тело, рекомендуется выбирать ось проецирования по направлению вектора 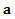ускорения тела.

В интегральной форме второй закон Ньютона имеет вид

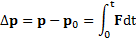
где 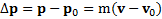– изменение импульса тела за время t, интеграл 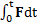называют импульсом результирующей силы 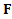за время ее действия t. Если 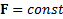, то .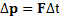

Третий закон Ньютона. Два тела взаимодействуют с силами, равными по величине и противоположными по направлению, лежащими на одной прямой: 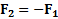либо 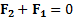или в скалярной форме 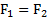. Во второй закон Ньютона входит одна из этих сил, приложенная к телу, движение которого изучается. Однако, если по постановке задачи тело входит в систему тел, то силы 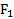и 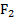становятся внутренними (взаимно уравновешивающимися: 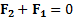) и не войдут во второй закон Ньютона.

Третий закон Ньютона используют для нахождения косвенным образом сил, приложенных к телам, для которых нельзя написать второй закон Ньютона, например, натяжения нити или веса тела.

Вес тела P – это сила, с которой тело действует на связь (опору или нить). По третьему закону Ньютона 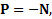где 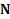– реакция связи. Вес тела приложен к связи, а не к телу.

Пример 1: Тело массой m брошено с поверхности земли с начальной скоростью 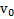под углом α к горизонту. Найти изменение импульса тела за время t его полета.

Дано: m, g, t, 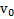, α. Найти: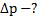

Решение: Наиболее простым будет решение при использовании второго закона Ньютона в интегральной форме (рис.23): 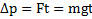. Если t есть время полета тела до его падения на землю, то .

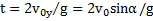Рис.23

Кинематическое решение задачи будет очень сложным, так как потребует нахождения сторон 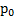и p векторного треугольника импульсов тела, угла 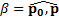между векторам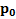и и 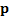и применения теоремы косинусов для нахождения стороны 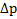этого треугольника. Окончательная формула для 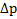окажется при этом очень громоздкой. Догадаться, что она упрощается, и упростить ее будет довольно непростой задачей.

Пример 2: Тело массой 0,5 кг соскальзывает с наклонной плоскости высотой 4 м и углом наклона 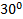за 4 с. Найти коэффициент трения тела о плоскость и выделившееся при соскальзывания тела тепло.

Дано: 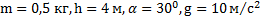. Найти: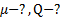

Решение: К телу приложены: сила тяжести mg, реакция Nнаклонной плоскости, сила трения 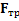(рис.24).

Рис.24

Выберем направление оси X параллельно наклонной плоскости в направлении ускорения тела a, а оси Y – перпендикулярно к ней. Если тело не вращается, то выбор положения О начала системы отсчета XOY не имеет значения.

Длина наклонной плоскости 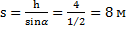. Ускорение тела 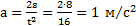. Найдем ускорение тела, используя второй закон Ньютона. Проецируя действующие на тело силы на оси X и Y выбранной СО (рис.24), получим:

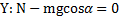или , .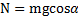

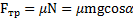X: 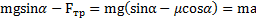,отсюда

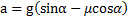,и

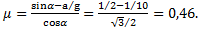
Выделившееся при соскальзывании тела тепло равно работе силы трения:

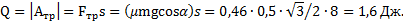
Ответ:

Пример 3. Два тела массой 2 кг и 3 кг связаны нитью и лежат на горизонтальной плоскости. К одному из этих тел приложена сила 10 Н, направленная под углом 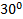к плоскости. Найти ускорение, с которым будут двигаться тела, и натяжение нити, связывающей их. Коэффициент трения между телами и плоскостью равен 0,1.

Дано: 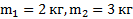, , 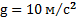, 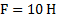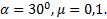Найти: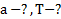

Решение: Будем считать, что сила 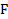приложена к телу массой 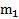. Выберем систему координат XOY стандартным образом, направив ось X по направлению ускорения тела a.Проецируя силы, действующие на тела системы, на оси X и Y выбранной системы отсчета, получим (рис.25):

Y: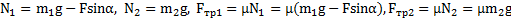

При объединении двух тел в единую систему второй закон Ньютона для них (в этом случае реакции нитей 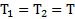станут внутренними силами и не войдут в закон) в направлении оси Xбудет иметь вид

X: ,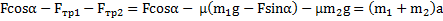

или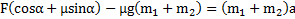

Отсюда ускорение тел .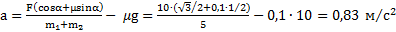

Рис.25

Натяжение нити 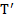не входит во второй закон Ньютона, так как приложено к нити, а не к телам. Но по третьему закону Ньютона оно равно реакции нитей 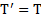. Реакции 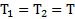нитей найдем, написав второй закон в направлении оси X для каждого тела в отдельности:

X: ,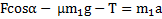

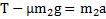
Второе уравнение проще. Из него получим .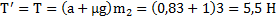

Можно было также при нахождении реакции нити T, подставив в полученную формулу выражение для ускорения a тела, получить формулу 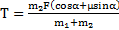. Но при построении решения задачи в виде последовательного алгоритма этого можно не делать.

Если сила F приложена к телу массой 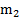, то получим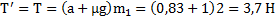

Ответ: 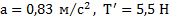, если сила F приложена к телу 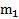, либо 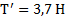, если сила F приложена к телу .

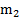Пример 4.Телу, лежащему в основании наклонной плоскости с углом наклона 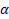, сообщают начальную скорость 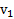вдоль наклонной плоскости, направленную вверх. После подъема до максимальной высоты оно возвращается к основанию наклонной плоскости. Чему равно отношение ускорений подъема и скатывания тела с наклонной плоскости? На какую максимальную высоту поднимется тело и с какой скоростью оно вернется к основанию наклонной плоскости, если коэффициент трения тела о плоскость равен ?

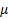Дано: 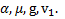Найти: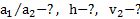

Решение: Второй закон Ньютона при движении тела вверх или вниз вдоль наклонной плоскости имеет вид 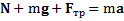.При движении тела вверх по наклонной плоскости его движение будет замедленным, а при движении вниз – ускоренным.В обоих случаях векторы ускорения тела 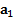и 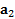будут направлены параллельно наклонной плоскости вниз.

Рис.26

При движении тела вверх или вниз реакция наклонной плоскости и сила трения, действующая на него одинаковы и равны , .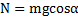

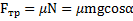При движении тела вверх (рис.26)второй закон Ньютона в проекциях на направление ускорения 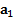тела имеет вид: 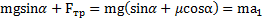. Откуда ускорение тела

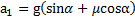
При движении тела вниз (рис.26)изменится лишь направление силы трения на противоположное и второй закон Ньютона для него в проекциях на направление его ускорения 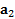будет иметь вид: 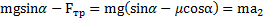. Откуда ускорение тела при его скатывании

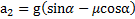
Отношение ускорений тела при его движении вверх и вниз равно

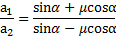
Путь, проходимый телом до точки его максимального подъема 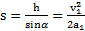. Откуда высота его максимального подъема .

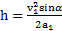Пути, проходимые телом вверх и вниз при его возврате в исходную точку одинаковы: 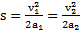, откуда скорость возврата тела к основанию наклонной плоскости .

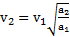Ответ: , ,, .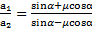

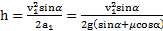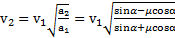Пример 5.Телу, лежащему в основании наклонной плоскости с углом наклона 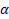, сообщают начальную скорость 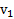вдоль наклонной плоскости, направленную вверх. Коэффициент трения тела о плоскость равен 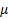. Через какое время тело вернется в исходную точку? Каково отношение времен подъема и соскальзывания тела?

Дано: 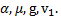Найти: ,

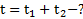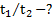
Решение: Ускорения 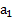и 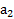при движении тела вверх и вниз по наклонной плоскости и скорость его возврата к ее основанию 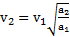найдены в примере 3. Тогда, обозначив 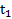время движения тела вверх до точки его максимального подъема и 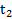– время его соскальзывания с наклонной плоскости, получим для времени t возврата тела в исходную точку

.

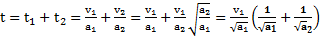Путь, проходимый телом вверх и вниз вдоль наклонной плоскости одинаковый: 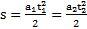, откуда отношение времен подъема и соскальзывания тела .

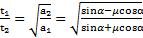Ответ: 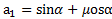, , , .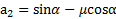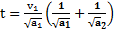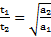