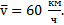Сложное поступательно-вращательное движение тела

Для описания поступательно-вращательного движения тела выбирают произвольную точку О, называемую полюсом (она является началом некоторой движущейся системы отсчета), скорость 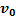поступательного движения которой известна. Эту поступательную скорость 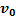приписывают всем точкам тела. Дополнительно произвольная точка тела вращается вокруг полюса О с угловой скоростью ωи линейной вращательной скоростью 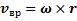, где r – вектор, проведенный из полюса О в рассматриваемую точку тела. Согласно обозначениям предыдущего раздела 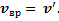Полная скорость точки тела с учетом ее поступательного и вращательного движений в неподвижной системе отсчета равна

.

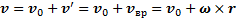Наиболее простым будет описание сложного движения, если полюс О выбрать в центре масс С тела, в этом случае 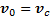, либо на мгновенной оси вращения, под которой понимают ось, проходящую через точку, скорость которой в любой момент времени равна нулю: 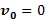. В неподвижной системе отсчета эта точка перемещается, изменяя свое положение в пространстве. Вокруг мгновенной оси вращения все точки тела совершают в любой момент времени чисто вращательное движение со скоростью 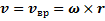, вектор 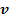которых перпендикулярен радиус-вектору r, проведенному из полюса О на мгновенной оси вращения в рассматриваемую точку.

Для тела, совершающего сложное движение, мгновенная ось вращения всегда существует и может с течением времени менять свое положение в пространстве и находиться вне или внутри тела, а также на его границе. При качении круглого тела по горизонтальной или наклонной плоскости без проскальзывания мгновенная ось вращения находится в точке касания тела и плоскости. В неподвижной системе отсчета она перемещается в пространстве. Знание положения мгновенной оси вращения упрощает решение многих задач механики.

Пример 1. Диск катится по горизонтальной поверхности со скоростью 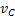. Найти скорости точек A и B, лежащих на ободе диска на его вертикальном и горизонтальном диаметрах.

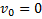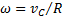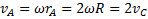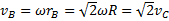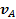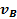Решение: Наиболее простым будет решение, если полюс О выбрать на мгновенной оси вращения (рис.10). Из-за отсутствия проскальзывания эта ось находится в точке касания плоскости и диска, ее скорость . Вокруг мгновенной оси все точки тела совершают чисто вращательное движение с угловой скоростью . Для скоростей точек A и B получим , . Векторы скорости и направлены перпендикулярно к векторам 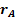и 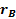, проведенным из точки О в точки A и B.

Рис. 10

Рис.11

Второй способ решения получим, взяв полюс в центре С диска (рис.11), движущегося со скоростью 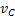. В этом случае все точки диска движутся вперед со скоростью 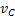и вращаются вокруг точки С с угловой скоростью 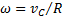, одинаковой для всех параллельных осей вращения. Линейные вращательные скорости всех точек на ободе диска направлены касательно к нему, одинаковы по величине и равны 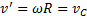. Складывая векторы поступательных и вращательных скоростей геометрически, получим согласно рис.11 для скоростей точек A и B на ободе диска 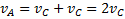, 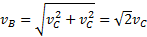. Скорость точки О касания тела и плоскости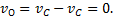

Ответ: .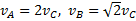

Пример 2. Две параллельные рейки движутся в одну сторону с постоянными скоростям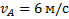и и 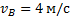. Между рейками зажат диск радиусом 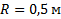, катящийся по рейкам без проскальзывания. Найти скорость центра С диска и угловую скорость его вращения, а также положение мгновенной оси вращения относительно центра С диска.

Дано: 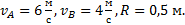Найти: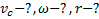

Решение: Выберем начало движущейся со скоростью 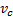системы отсчета в центре С диска, ось X в направлении движения реек, а ось Y перпендикулярно к ней.

Рис.12

Скорости вращательного движения точек A и B диска относительно центра С диска одинаковы по величине 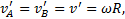но противоположны по направлению (рис.12), поэтому скорости этих точек в неподвижной системе отсчета будут равны

Это система двух уравнений относительно двух неизвестных 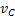и 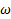, решая которую, получим

.

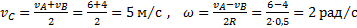Для нахождения положения мгновенной оси вращения О относительно центра С диска необходимо учесть, что в неподвижной СО скорость точки О 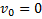, а угловая скорость вращения ω относительно любых параллельных осей одинакова. Имеем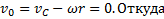

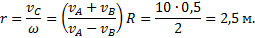
Ответ: 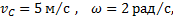мгновенная ось вращения О находится от точки С в направлении CB на расстоянии r=2,5 м.

6. Среднее значение физической величины. Средняя скорость и ускорение.

Под средним значением функции 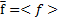на интервале 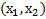понимают отношение площади 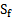под графикомэтой функции на этом интервале к величине 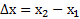этого интервала (рис.13).

Рис.13

Согласно математическому анализу площадь 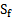под графиком функции 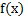– это определенный интеграл от этой функции на данном интервале 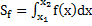. Имеем по определению

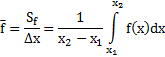
Из этого определения следует, что средние значения скорости и ускорения 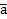тела на временном интервале 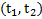равны

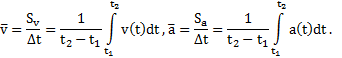
В большинстве задач площади 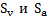под графиками функций 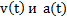могут быть вычислены по формулам геометрии (формулам площадей прямоугольника, треугольника и трапеции), не прибегая к интегрированию. Поэтому первичным при нахождении средних значений функций является построение графиков этих функций.

Интегральные представления средней скорости и ускорения 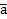, исходя из определений пути s и скорости v тела, могут быть записаны в виде

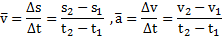
Здесь 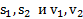значения функци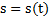й и 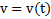в моменты времен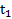и и .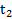

При движении с постоянным ускорением .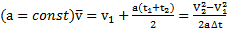

Если функция имеет вид прямой линии 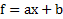(и только в этом случае), ее среднее значение может быть вычислено как 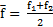, где 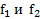―значения функции 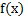на концах промежутка усреднения 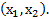Эта формула легко доказывается графически, исходя из формулы площади трапеции. Отсюда следует: если тело движется с постоянным ускорением 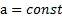, то его скорость ―линейная функция времени 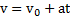, и ее среднее значение на интервале времени 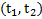может быть вычислено по формуле

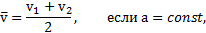
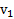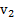где и скорости тела в моменты времен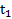и и 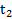на концах промежутка усреднения.

Средние значения угловых величин определяются аналогичным образом при замене параметров 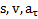на .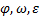

Пример 1. Тело движется по закону 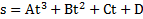. Найти его среднюю скорость и среднее ускорение на интервале времени .

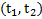Дано: 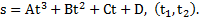Найти: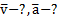

Решение: Скорость тела 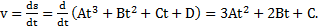Согласно определению средняя скорость и среднее ускорение 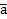тела будут равны

,

.

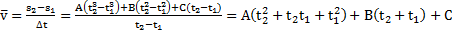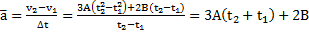Ответ:

Пример 2. Автомобиль начинает двигаться и за время 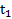увеличивает свою скорость до значенияравногоv. Далее он движется с этой скоростью в течение времени 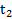, а затем начинает тормозить и через время 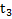останавливается. Найти средние значения скорости и ускорения автомобиля за все время его движения.

Дано: 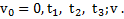Найти: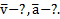

Решение: Ускорения автомобиля на всех участках его движения: 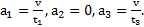Зависимости скорости автомобиля от времени имеют вид:

.

Построим графики зависимостей 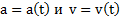и вычислим средние значения скорости и ускорения тела графически.

Рис.14

График зависимости 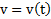имеет вид трапеции (рис.14) с основаниями 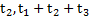и высотой v. Площадь этой трапеции 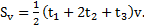Тогда средняя скорость автомобиля за все время 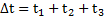его движения

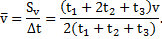
Если 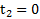, то 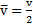независимо от времени разгона и торможения автомобиля.

Аналогично графически вычисляется среднее ускорение автомобиля (рис.15). С учетом 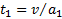и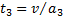

.

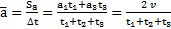Ответ: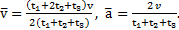

Рис.15

Пример 3. Автомобиль, двигаясь равноускоренно, изменяет свою скорость от 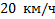до 100 км/ч. Найти среднюю скорость автомобиля за время его разгона.

Дано: 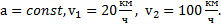Найти: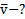

Решение: При движении тела с постоянным ускорением 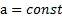его средняя скорость может быть вычислена по формуле

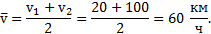
Ответ: