К и н е м а т и к ап о с т у п а т е л ь н о го и в р а щ а т е л ь н о г о д в и ж е н и я

МЕХАНИКА

Учебное пособие для самостоятельной работы

По курсу физики

Санкт-Петербург

Механика. Учебное пособие для самостоятельной работы по курсу физики.

Альтмарк А.М., В.М. Вяткин, В.В.Морозов, Посредник О.В.

Под редакцией.

Содержит основные формулы и примеры решения задач по курсу «Общая физика», раздел «Механика». Предназначено для студентов 1-го курса технических факультетов СПбГЭТУ «ЛЭТИ».

О Г Л А В Л Е Н И Е

Стр.

К И Н Е М А Т И К АП О С Т У П А Т Е Л Ь Н О ГО И В Р А Щ А Т Е Л Ь Н О Г О Д В И Ж Е Н И Я

Поступательное движение 7

Вращательное движение 16

Связь между линейными и угловыми величинами 17

Относительное движение 18

Сложное поступательно-вращательное движение тела 21

Среднее значение физической величины. Средняя скорость и ускорение 23

Д И Н А М И К А П О С Т У П А Т ЕЛ Ь НО Г О Д В И Ж Е Н И Я

Центр масс тела и системы тел 26

Силы в механике 31

9. Законы Ньютона 35

Второй закон Ньютона в неинерциальной системе отсчета. Силы инерции 40

Второй закон Ньютона для вращающегося тела 46

Второй закон Ньютона для системы тел 48

Закон сохранения импульса системы тел и положения ее центра масс 49

Столкновения тел 52

Работа и мощность силы. Диссипативные силы 53

Теорема о кинетической энергии тела или основная теорема механики 54

Консервативные силы. Потенциальная энергия тела в поле консервативной

Силы 57

Связь между потенциальной энергией и консервативной силой 57

Потенциальная энергия взаимодействия тел 57

Полная механическая энергия тела. Закон сохранения полной механической 58 энергии

Гидростатика и гидродинамика 59

Д И Н А М И К А В Р А Щ А Т ЕЛ Ь Н О Г О Д В И Ж Е Н ИЯ

Моменты силы и импульса тела 64

Момент инерции материальной точки и тела. Теорема Штейнера 64

Уравнение моментов или основное уравнение динамики вращательного

Движения 75

Закон сохранения момента импульса 80

Работа и мощность момента силы 82

Кинетическая энергия вращающегося тела 83

К О Л Е Б А Т Е Л Ь Н О Е Д В И Ж Е Н И Е

Гармонические колебания 88

Определение начальной фазы колебаний 90

Уравнение гармонического осциллятора. Собственные частоты и периоды колебаний математического, физического и пружинного маятников 91

Кинетическая, потенциальная и полная энергия колеблющегося тела 93

Затухающие колебания. Уравнение гармонического осциллятора с затуханием 94

Характеристики колебательной системы с затуханием 96

Вынужденные колебания 97

Введение.

Вы поступили в ЛЭТИ, чтобы получить высшее образование. Это значит, что Вами принято мотивированное решение за годы учебы в университете овладеть знаниями и умениями, необходимыми для начала самостоятельной деятельности. И, конечно же, чем лучше удастся претворить в жизнь принятое решение, тем быстрее и успешнее пойдет Ваша карьера, тем интереснее будет работать, тем выше будет качество Вашей жизни.

Тем не менее, среди студентов, часто бытует мнение, что профессиональные знания и умения они получают только при изучении специальных дисциплин. Это – заблуждение. Фундаментальные знания являются основой для успешного изучения специальных дисциплин. Нельзя построить здание на песке, нельзя получить профессиональные знания и умения без фундаментальных дисциплин.

Физика занимает особое место в подготовке специалиста с высшим образованием. В государственном образовательном стандарте приведены квалификационные характеристики специалиста, а также перечень знаний и умений, необходимых для начала самостоятельной деятельности. Спросите любого успешного специалиста, и он Вам скажет, что основы большинства этих знаний и умений формируются при изучении физики.

Более того, специалисту с высшим образованием необходимо постоянно решать различные задачи: технологические, конструкторские, исследовательские. Причем, в процессе самостоятельной деятельности приходится не только искать способ решения этих задач, но и формулировать технические задания для себя и других, т.е. составлять условия задачи.

Именно поэтому среди компетенций, необходимых специалисту с высшим образованием, важная роль уделяется познавательной деятельности (умение учиться – это тоже задача, которую каждый решает для себя), экспериментальной деятельности (умение выбрать методику, правильно организовать измерения и грамотно обработать их результаты), грамотному выполнению расчетов. В этом перечне легко заметить основные виды занятий, которые проводятся при изучении курса физики в вузе. Будьте уверены, что чем раньше Вы начнете вырабатывать в себе соответствующие умения и навыки, тем лучше Вы будете подготовлены к дальнейшему обучению и самостоятельной работе.

Изучив курс физики, Вы поймете, что физика обладает той особенностью, что методы, принципы и понятия, используемые в физике, так или иначе присутствуют практически в любой дисциплине (и не только инженерной), таким образом, изучая физику, студент приобретает элементарные навыки ремесла, которые, часто интуитивно, позволяют специалисту применить тот или иной технический прием в своей работе. Однако, достигнуть этого можно лишь в результате упорного труда, систематического, целенаправленного и самостоятельного

Учебное пособие, которое Вы сейчас читаете, как раз и предназначено для правильной организации самостоятельной работы и подготовки к лабораторно-практическим занятиям, в той их части, где требуется выполнение индивидуального домашнего задания.

В этой книге собран материал, относящийся к разделам «Молекулярная физика», «Основы термодинамики», «Элементы статистической физики», «Явления переноса». Пособие построено таким образом, что разбираемые задачи постепенно усложняются в каждом разделе, так, что последние в списке задачи несколько выходят за рамки стандартной программы нашего университета. Тем не менее, мы рекомендуем ознакомиться и с этими задачами, хотя для выполнения индивидуального задания, на наш взгляд, достаточно понять несколько первых задач в каждом разделе. Мы надеемся, что среди читателей этой книги есть любознательные студенты, интересующиеся физикой.

При внимательном анализе разного рода задач по различным разделам курса и дисциплинам можно отчетливо видеть, что различие их между собой состоит только в содержании и цели, а по характеру деятельности, нужной для решения, все они практически одинаковы. Более того, сравнительный анализ приемов решения производственных и учебных задач показывает, что они имеют сходную структуру, иначе говоря, при решении любой задачи необходимо выполнять одни и те же этапы.

1. Анализ содержания задачи, краткая запись условий и требований.

2. Поиск способа решения задачи и составление плана решения.

3. Решение задачи, проверка правильности решения, оформление решения.

4. Анализ выполненного решения, отбор информации, полезной для будущей деятельности.

Общие приемы, которые вырабатываются у Вас в процессе учебы, и практического решения учебных задач, позволят Вам освоить общий подход к решению задач любого типа, ознакомиться с основными особенностями каждого из этапов процесса решения. В конечном итоге Вы получите умения, необходимые для самостоятельной работы, т.е. овладеете тем, что сейчас называют «практико-ориентированной» подготовкой.

В этом. Вам поможет серия учебных пособий, подготовленных ведущими преподавателями кафедры

Поступательное движение

Существуют следующие методы описания поступательного движения тела (материальной точки): энергетический, векторный, координатный и естественный.

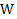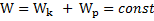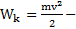Энергетический подход к решению задач кинематики.В этом подходе используется закон сохранения полной механической энергии, согласно которому, если тело движется только в поле консервативных сил (в большинстве задач достаточно знать, что на тело не действуют силы трения), то его полная механическая энергия сохраняется: , где кинетическая энергия тела, 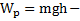потенциальная энергия тела в поле силы тяжести земли, m – масса тела, v – его скорость, h – высота тела над поверхностью земли, g – ускорение свободного падения.

Для двух произвольных точек траектории при движении тела в поле силы тяжести закон сохранения энергии имеет вид

,

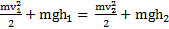Откуда .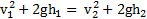

Отсюда следует, что независимо от траектории движения тела на одной и той же высоте 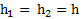оно имеет одинаковую скорость 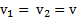. Направления векторов скорости 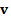тела в разных точках траектории могут быть при этом разными.

Если учесть, что 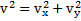,где 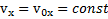, то можно написать закон сохранения энергии в направлении оси Y

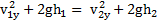
Пример 1. Тело брошено с высоты 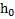под некоторым углом α к горизонту с начальной скоростью 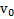(рис.1). Найти скорость падения тела на землю, его максимальную высоту подъема 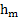и направление 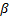вектора его скорости к горизонту при падения на землю. Зависит ли скорость падения тела на землю от угла α его броска к горизонту?

(рис.1)

Дано:1) .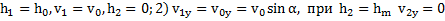

Найти: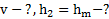

Решение: Согласно закону сохранения энергии для точек броска и падения тела на землю

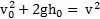скорость падения тела на землю .

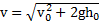Используя закон сохранения энергии в направлении оси Y для точек броска и

максимальной высоты подъема тела 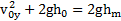, найдем

.

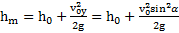Угол 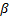падения тела на землю определяется условием .

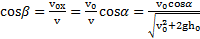Ответ: независимо от угла α броска тела оно упадет на землю с одной и той же скоростью 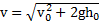. Однако направления 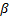к горизонту векторов скорости 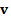тела при разных углах α его броска при его падении на землю будут разными и определяются условием 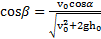. Максимальная высота подъема тела .

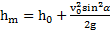Вращательное движение

Вращательное движение тела описывается углом поворота тела 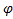, его угловой скоростью ω и угловым ускорением ε , которые являются аналогами величин s, v, 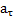, используемыми для описания поступательного движения тела. Согласно определению

.

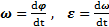Параметры 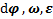являются векторами. Направление векторов 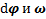совпадает с направлением оси вращения тела (рис.7) и связано с ним правилом правого винта: если правый буравчик вращать по направлению вращения тела, то направление его движения укажет направление векторов 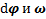.Вектор ε в случае фиксированной неподвижной оси вращения также направлен вдоль оси вращения. Он параллелен вектору ω при ускоренном вращении тела и антипараллелен ему при его замедленном вращении.

Рис.7

Элементарный поворот dϕтела всегда вектор, однако угол поворота тела 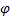является вектором только при вращении тела вокруг фиксированной оси его вращения.

Изменение угловой скорости тела Δω и угол 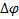его поворота за время вращения тела t равны

,

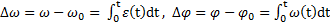где 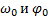– начальная угловая скорость и начальное угловое положение тела при t=0.

При вращении тела с постоянным угловым ускорением 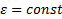уравнения вращательного движения имеют вид

.

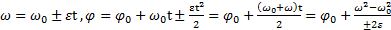где +ε и –ε соответствуют ускоренному и замедленному вращению тела.

Наряду с угловыми величинами 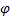(рад) и ω (рад/с) для описания вращательного движения используются величины N (об) – число оборотов тела и n (об/с) – частота вращения тела, определяемые соотношениям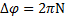и и 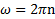. В терминах этих величин уравнения вращательного движения при 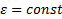имеют вид

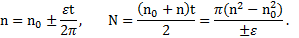
Однако, если ε=0 и 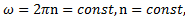то 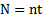.Только в этом случае частота вращения тела может рассчитываться по формуле 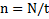и можно ввести понятие периода T вращения тела (n=1/T). Это можно отнести к описанию вращения Земли вокруг своей оси.

3. Связь между линейными и угловыми величинами

Угловые величины 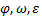для всех точек вращающегося тела относительно любых параллельных осей вращения одинаковы, а линейные величины 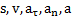различны. Для установления связи между ними используют определение радианной меры угла 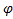, опирающегося на дугу длиной s окружности радиуса R: 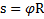и определения линейных величин. В результате получим следующие уравнения связи

,

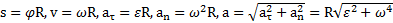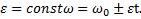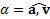где в случае Угол между векторами aи vв некоторый момент времени t определяется соотношением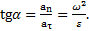

рис.8

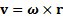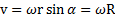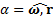В теории представляет интерес векторная связь между векторами vи ω: , гдеr -вектор, проведенный из произвольной точки О на оси вращенияZ в произвольную точку вращающегося тела (рис.8). Направления векторов v и ωcвязаны между собой правилом правого винта. Переходя к скалярной форме, получим , где – угол между векторами ω и r, 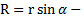расстояние от рассматриваемой точки тела до его оси вращения Z или радиус окружности, по которой эта точка вращается.

Пример 1. Тело, вращающееся по окружности радиуса R с постоянным угловым ускорением, увеличило свою частоту вращения от 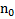до оборотов в секунду, совершив при этом 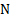оборотов. Найти угловое ускорение вращения тела и время его вращения, угол его поворота, начальную и конечную угловые скорости. Чему равны путь, пройденный телом вдоль окружности, его начальная и конечная скорости, касательное, центростремительное и полное ускорение?

Дано: 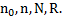Найти: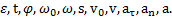

Решение:Построим решение задачи в виде последовательного алгоритма. Число оборотов N тела при 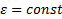дается уравнениями

.

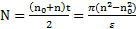Откуда находим угловое ускорение и время вращения тела

.

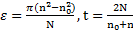Угол поворота и угловые скорости тела: 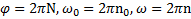. Линейные величины: .

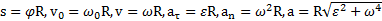Ответ: , ,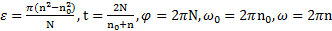

.

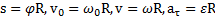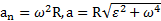Относительное движение

Рассмотрим произвольную неподвижную систему отсчета XOY с началом в точке О, и движущуюся систему отсчета 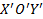, положение начала координат которой 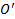относительно точки О задается радиус-вектором 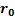, а точка 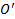движется относительно XOY со скоростью 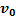и ускорением 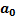.Обозначим через 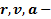положение, скорость и ускорение некоторой точки (она может принадлежать и твердому телу) в системе координат XOY, а через 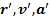те же параметры этой точки в системе координат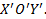

Рис.9

Учитывая, что 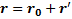(рис.9) и последовательно дифференцируя по времени обе части этого равенства, придем к следующим уравнениям связи

между скоростями 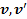и ускорениями 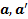рассматриваемойточки в неподвижной и движущейся системах отсчета.

Движение в неподвижной СО называют также абсолютным, движение подвижной СО относительно неподвижной – переносным, а движение тела в движущейся СО – относительным.

Пример 1. Тело, движущееся со скоростью 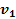, сталкивается абсолютно упруго с движущейся со скоростью 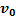вертикальной массивной стенкой. Найти скорость тела после соударения со стенкой.

Дано: 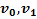. Найти: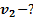

Решение: Будем считать стенку, движущуюся со скоростью 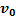, движущейся системой отсчета. Обозначим 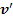скорость тела в этой системе отсчета.Тогда скорость те 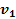ладо его столкновения

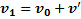.После столкновения со стенкой тело вследствие абсолютно упругого удара приобретет относительно стенки скорость 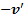, и его скорость станет равной 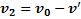.Из этих двух уравнений получим: .

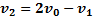В проекциях на направление движения тела и стенки при их встречном движении получим 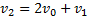. В случае же движения стенки и тела в одном направлении 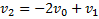. Отсюда следует: если стенка движется от тела со скоростью 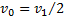, то тело после столкновения с ней остановится 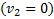.Чтобы тело отскочило от удаляющейся стенки, она должна удаляться от него со скоростью .

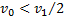Ответ: .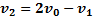

Пример 2.Скорость струи пара перед попаданием на лопатки паровой турбины равна 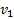. Какой должна быть скорость 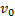лопаток, чтобы вся кинетическая энергия струи пара могла перейти в энергию вращения турбины?

Решение: Чтобы вся кинетическая энергия струи пара перешла в энергию вращения турбины, его скорость после отражения от лопаток должна равняться нулю 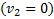. Согласно примеру 1 получим 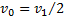. Это соотношение выполняется в рабочем режиме турбины.

Ответ: .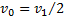

Пример 3. Два автомобиля движутся по одной дороге. Скорость первого автомобиля , а второго – . Найти относительную скорость движения автомобилей при их движении в одном направлении и навстречу друг другу.

Дано: 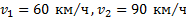. Найти: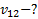

Решение: Свяжем с первым автомобилем движущуюся СО. Тогда 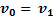, а относительная скорость второго автомобиля относительно первого 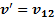, его абсолютная скорость относительно земли 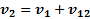. Откуда относительная скорость автомобилей .

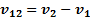При движении автомобилей в одном направлении в проекциях на направление их движения получим 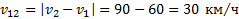. При встречном движении автомобилей в проекциях на направление движения любого из автомобилей: .

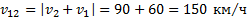Ответ: 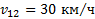при движении автомобилей в одном направлении, 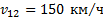при встречном движении автомобилей.

Пример 4. Два тела бросают с поверхности земли вертикально вверх с начальными скоростям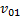и и 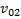с задержкой по времени, равной τ. Найти относительную скорость движения тел в произвольный момент времени.

Дано: 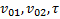. Найти: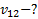

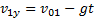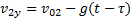Решение: проекции абсолютных скоростей тел на вертикальное направление их движения равны и . Проекция относительной скорости тел на вертикальное направление 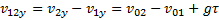. Относительная скорость тел 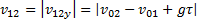в любой момент времени одинакова.

Ответ: .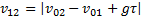

Пример 5. Два тела движутся в одной плоскости, их скорости изменяются по закону 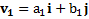, 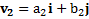. Найти скорость движения их ЦМ, импульс системы и скорости тел относительно их ЦМ. Отличаются ли относительные скорости тел в неподвижной СО и в системе их ЦМ?

Дано: 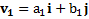, 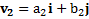. Найти: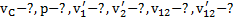

Решение:Система понятий, используемых в данной задаче, введена в разделах7 и 12 (Центр масс и второй закон Ньютона для системы тел).Задачу будем решать в векторной форме. Скорость ЦМ системы двух точек

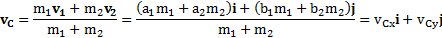
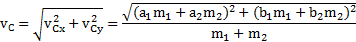
Импульс системы совпадает с импульсом ее ЦМ: .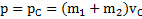

Если скорость тела относительно ЦМ 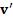, а скорость ЦМ относительно земли 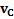, то скорость тела относительно земли 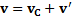, откуда 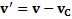. В частности,

,

,

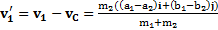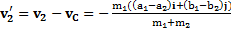
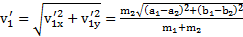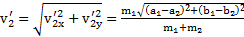
Скорости тел относительно друг друга в неподвижной СО и системе ЦМ

,

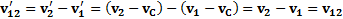то есть относительные скорости тел в обеих системах отсчета одинаковы.

Ответ: , , ,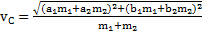

, .

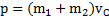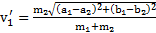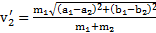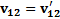Силы в механике

Сила – это векторная мера взаимодействия тел (скалярной мерой взаимодействия является потенциальная энергия тела ).

Любая сила характеризуется ее величиной, направлением и точкой приложения. Осуществлять параллельный перенос начал векторов сил, действующих на тело, в одну точку в задачах на поступательное движение тела нежелательно, а в задачах на вращательное движение тела вообще нельзя, так как это приведет к неправильному решению задачи.

К механическим силам, действующим на тело, относятся:

1. Реакции связейN, T, R и т.д. Связь (опора) – это любое тело, ограничивающее движение другого тела (поверхность какого-либо тела, нить). Реакции связей не имеют конкретного способа вычисления и их находят из второго закона Ньютона.

2. Сила трения скольжения , где μ – коэффициент трения тела о поверхность связи,N – нормальная реакция связи. Силу трения покоя находят из условия равновесия тела на поверхности. Силу трения качения и скольжениятела находят из основных динамических принципов: второго закона Ньютона или основного закона динамики вращательного движения.

3. Гравитационная сила или сила тяжестисогласно закону всемирного тяготения Ньютона

где γ – гравитационная постоянная, M и m – гравитационные массы взаимодействующих тел, r –расстояние между их центрами. Если M – масса планеты, то g – это ускорение свободного падения на расстоянииr от центра планеты. Для планеты радиуса R (для Земли ) ускорение свободного падения на высоте h от поверхности планеты равно

где – ускорение свободного падения на поверхности планеты. Для Земли Масса тела, входящая в закон всемирного тяготения, называется гравитационной, а входящая во второй закон Ньютона – инертной. Это разные массы. Равенство единиц измерения инертной и гравитационной масс достигается соответствующим опытным выбором гравитационной постоянной

Рис.33

На наклонную плоскость действует сила тяжести 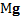и сила давления 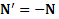тела на нее, и второй закон Ньютона для плоскости в неподвижной СО будет иметь вид .

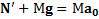Для решения задачи выберем две СО: неподвижную XOY, связанную с поверхностью, на которой находится наклонная плоскость, ось X которой направлена по ускорению 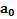наклонной плоскости, и движущуюся СО 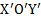, связанную с движущейся наклонной плоскостью, ось 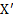которой направлена по ускорению 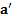соскальзывания тела с наклонной плоскости.

Спроецируем силы, действующие на тело, на ось 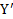движущейся СО. Получим

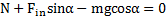. Откуда реакция наклонной плоскости, действующая на тело, и сила давления тела на плоскость равны

.

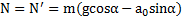Проецируя силы, действующие на наклонную плоскость, на ось X неподвижной СО, получим

.

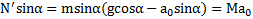Откуда ускорение наклонной плоскости .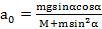

Второй закон Ньютона для тела в проекциях на ось 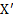движущейся СО будет иметь вид

.

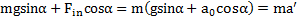Откуда ускорение 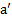, с которым тело соскальзывает с наклонной плоскости, будет равно

.

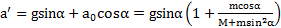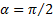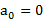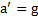При , как и должно быть, и . Ускорения плоскости и тела связаны соотношением .

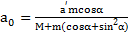Ответ: , , .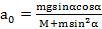

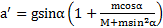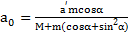Пример 8. Найти в примере 7 смещение наклонной плоскости по горизонтали после того как тело опустится на высоту h. Чему будут равны скорости тела и наклонной плоскости в этот момент времени?

Дано: 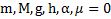.Найти: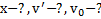

Решение:Путь, проходимый телом вдоль наклонной плоскости за время t, и смещение плоскости за это время описываются уравнениям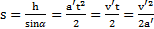и и 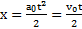. Откуда с учетом примера 7 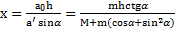. Скорость тела 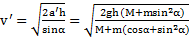, а наклонной плоскости ― .

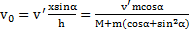Ответ: , , .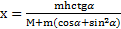

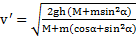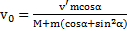Пример 9. Решить задачу в примере 7 в предположении, что между телом и наклонной плоскостью действуют силы трения. Коэффициент трения между телом и плоскостью равен μ.

Дано: 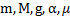.Найти: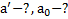

Решение:Согласно примеру 7 силы трения (рис.33), действующие между телом и плоскостью равны

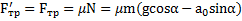
Второй закон Ньютона для наклонной плоскости в направлении оси Xбудет иметь вид:

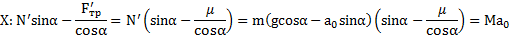
Откуда ускорение наклонной плоскости

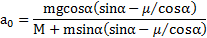
Второй закон Ньютона для тела в проекциях на ось 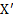движущейся СОбудет иметь вид:

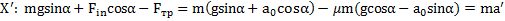
Откуда ускорение тела относительно наклонной плоскости

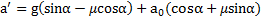
Ответ: , .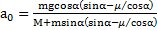

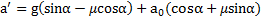Столкновения тел

Различают следующие виды соударений тел: абсолютно неупругое, частично-упругое и абсолютно упругое. Если процесс столкновения быстрый 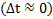, то имеет место закон сохранения импульса в системе сталкивающихся тел.

Абсолютно неупругое столкновение тел.При этом виде столкновения тела слипаются и после столкновения движутся вместе(рис.38).

Рис. 38

Любое столкновение тел описывается законом сохранения импульса и энергии. В данном случае, обозначив импульсы тел до и после столкновения 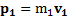, , 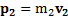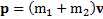и Q – выделившееся при ударе тепло,получим

.

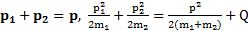Возведя первое равенство в квадрат, найдем квадрат импульса тел после столкновения, а из второго – выделившееся при ударе тепло

, ,

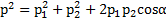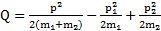где 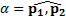– угол между векторами импульсов тел до их столкновения.

При прямом центральном ударе скорость тел после столкновения 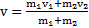, а выделившееся при ударе тепло

,

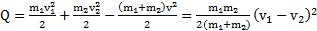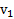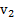где и – проекции скоростей тел 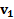и 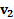на направление их движения и имеют знак .

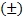Частично упругое столкновение тел.Ограничимся случаем лобового столкновения тел. При этом виде удара тела не слипаются, но после столкновения у них имеется остаточная деформация (вмятины) и выделяется при ударе тепло 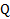. Законы сохранения импульса в проекциях на направление движения тел и энергии в этом случае будут иметь вид

,

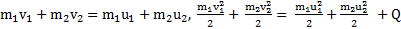где 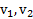и 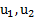– скорости тел до и после их столкновения.

Абсолютно упругое столкновение тел. При этом виде столкновения тела после столкновения восстанавливают свою форму и остаточная деформация у них отсутствует, поэтому выделившееся при ударе тепло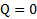

Рис.39

Система уравнений, описывающая удар (рис.39), будет иметь вид

, .

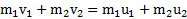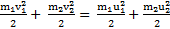Эту систему уравнений можно свести к линейной. Для этого перенесем члены с