Главное n, орбитальное l и магнитное m квантовые числа; их физический смысл.

Процесс нахождения решения, как это мы продемонстрировали на примере решения уравнения Шредингера для частицы в потенциальной яме, связан с нахождением собственных значений и собственных функций. Можно показать, что в данном случае уравнение имеет однозначные, конечные и непрерывные решения

1) при любых Е >0 , что соответствует свободно движущемуся электрону из ∞ на ∞, пролетающему вблизи ядра;

2) при Е< 0, что соответствует электрону, связанному с ядром. Эти отрицательные значения энергии дискретны и равны

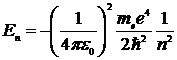, n =1,2,3,…

где n - главное квантовое число.

Эти значения получены при строгом решении уравнения Шредингера и полностью совпадают со значениями энергии водородоподобного атома из теории Бора. Однако в данном случае значения энергии получаются как следствие выполнения основных законов квантовой механики, в то время как Бору для получения такого результата пришлось вводить специальные дополнительные предположения. Очевиден физический смысл главного квантового числа - это номер энергетического уровня, а не номер боровской орбиты.

Из соотношения неопределенностей Гейзенберга следует, что нельзя точно определить координаты и импульс электрона. Значит, нельзя ввести траекторию движения электрона в атоме. Теперь понятие орбит теряет смысл, их место занимает вероятность нахождения электрона в некотором объеме. Для этого необходимо найти волновую функцию электрона в данном состоянии, т.е. найти такую функцию координат 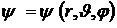, которая удовлетворяет уравнению Шредингера.

Решение ищется в виде

,

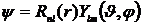где r – расстояние от ядра атома, R(r) – радиальная волновая функция зависит только от r, 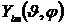- угловая волновая функция зависит только от углов θ,φ. Это говорит о том, что радиальное движение электрона и движение электрона вокруг ядра независимы.

Подстановка 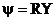в уравнение Шредингера приводит к тому, что будут существовать два независимых уравнения – для радиальной части R(r) и для угловой 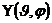. В результате решения уравнений собственные функции содержат три целочисленных параметра – n, l, и m.

Параметр l носит название орбитального (или азимутального) квантового числа. Значение этого параметра определяет квантование момента импульса электрона в атоме (рис.2) при данном значении энергии E_n

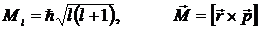
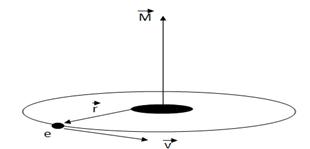
Рис.2

Решения, удовлетворяющие стандартным условиям, получаются лишь при значениях l , не превышающих n-1. Следовательно, при данном n квантовое число l может принимать n различных значений

l = 0,1,2,…, n -1.

Так как момент импульса – векторная величина, то он квантуется не только по величине, но и по направлению. Параметр m носит название магнитного квантового числа и определяет квантование проекции момента импульса M_z на произвольную ось Z

.

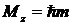При данном l квантовое число m может принимать 2l+1 различных значений

m = -l, - l +1, - l +2, …, - 1, 0, +1, …,l – 1, l/

Следовательно, каждому собственному значению энергии E_n (кроме Е₁) соответствует несколько собственных функций 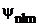, отличающиеся значениями квантовых чисел l и m. Это означает, что атом водорода может иметь одно и то же значение энергии, находясь в нескольких различных состояниях. Такие состояния мы определили как вырожденные. Кратность вырождения энергетического уровня, т.е. число различных состояний, соответствующих этому энергетическому уровню, можно вычислить, исходя из возможных значений для l и m, и она равна n².