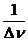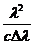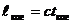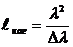Световых волн. Временная когерентность. Время и длина когерентности.
Интерференция света – пространственное перераспределение энергии светового излучения при наложении когерентных световых волн.
Когерентностью называется согласованное протекание двух или нескольких колебательных или волновых процессов (см. лекцию № 28, п.3).
Монохроматическое излучение (от греч. monos – один, единый и chroma – цвет) – электромагнитное излучение одной определенной и строго постоянной частоты. Происхождение термина связано с тем, что различие в частоте световых волн воспринимается человеком как различие в цвете. Отметим, что излучаемый реальным источником свет не может быть строго монохроматичным.
Различают временную и пространственную когерентность.
Временная когерентностьхарактеризует сохранение взаимной когерентности при временном отставании одного из лучей по отношению к другому.Мерой когерентностислужит время когерентности 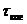 - максимально возможное время отставания одного луча по отношению к другому, при котором их взаимная когерентность еще сохраняется.
- максимально возможное время отставания одного луча по отношению к другому, при котором их взаимная когерентность еще сохраняется.
В идеализированном случае рассматривают интерференцию строго монохроматических волн с постоянной разностью фаз. Однако, такие волны бесконечны в пространстве, времени и, не существуют в природе. Поэтому интерференция монохроматических волн является лишь первым приближением в изучении интерференции волн от реальных источников.
Выясним роль немонохроматичности волн во временной когерентности.
При рассмотрении интерференции близкий к монохроматическому реальный свет можно представить как набор монохроматических составляющих – волн в интервале частот от ω до ω + Δω. где Δω – достаточно малая величина. Пусть волны, соответствующие крайним значениям спектрального интервала (ω; ω + Δω) вызывают в данной точке пространства (например, на экране) колебания 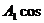 ωt и
ωt и 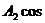 (ω + Δω)t (начальные фазы для простоты полагаем равными нулю). Если разность фаз составляющих (компонент) кратных частот в этой точке равна π, то это означает, что на «горб» от одной составляющей наложится «впадина» от другой крайней компоненты (ω + Δω) Интерференционная картина «смажется». Наглядно представить ситуацию можно следующим образом. Наложите ладонь одной руки на ладонь другой, палец на палец, а теперь сместите одну из ладоней на ширину одного пальца, картина интенсивности сладится.
(ω + Δω)t (начальные фазы для простоты полагаем равными нулю). Если разность фаз составляющих (компонент) кратных частот в этой точке равна π, то это означает, что на «горб» от одной составляющей наложится «впадина» от другой крайней компоненты (ω + Δω) Интерференционная картина «смажется». Наглядно представить ситуацию можно следующим образом. Наложите ладонь одной руки на ладонь другой, палец на палец, а теперь сместите одну из ладоней на ширину одного пальца, картина интенсивности сладится.
(Замечание. Рассмотрение промежуточных по частоте компонент между ω и ω + Δω не изменит качественной картины.)
Итак, время, за которое разность фаз компонент световой волны с верхней и нижней частотой составит порядка π и будет временем когерентности. Разность фаз этих колебаний Δφ = Δωt. Время когерентности определится из соотношения Δω 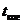 ≈π. Так как Δω = 2πΔν
≈π. Так как Δω = 2πΔν 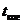 , то 2πΔν
, то 2πΔν 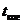 ≈π. Отсюда
≈π. Отсюда 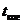 ≈1/2Δν, пренебрегая в наших оценках «двойкой», получим
≈1/2Δν, пренебрегая в наших оценках «двойкой», получим
|
.
От частоты перейдем к длине волны ν = с / λ. Продифференцируем последнее выражение: dν = – 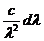 и заменим знак дифференциала d на Δ, полагая изменение λ конечным, но достаточно малым.
и заменим знак дифференциала d на Δ, полагая изменение λ конечным, но достаточно малым.
|
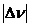 =
= 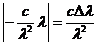 .
. Соответственно время когерентности
(32-1)
где Δλ – ширина интервала длин интерферирующих волн; чем меньше интервал Δλ, тем больше время когерентности.
Можно сказать, что в тех случаях, когда время фиксирования интерференционной картины 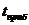 много больше времени когерентности накладываемых волн (
много больше времени когерентности накладываемых волн ( 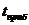 >>
>> 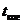 ), прибор не зафиксирует интерференции. Если же
), прибор не зафиксирует интерференции. Если же 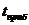 <<
<< 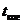 , прибор обнаружит четкую интерференционную картину.
, прибор обнаружит четкую интерференционную картину.
|
Подставляя (32-1), в последнюю формулу, получим
|
(32-2)
Таким образом, временная когерентность связана со степенью монохроматичности света, которая характеризуется отношением λ /Δλ.Чем больше
λ /Δλ, тем больше и степень монохроматичности, тем больше время и длина когерентности.
2. Пространственная когерентность. Радиус когерентности.
Пространственная когерентность волны характеризует наличие взаимной когерентности двух световых лучей, взятых из различных точек по сечению волны.
Мерой пространственной когерентности служит радиус когерентности – наибольший радиус круга, мысленно вырезаемый в поперечном сечении волны, при котором любые два луча, исходящие из различных точек внутри этого круга, еще остаются взаимокогерентными.
Если размеры источника значительно меньше длины световой волны, то всегда получается резкая интерференционная картина (лучи идут, по существу, из одной точки).
 В случае источника конечных размеров получаем, по существу, наложение многих интерференционных картин, создаваемых многими парами когерентных источников.
В случае источника конечных размеров получаем, по существу, наложение многих интерференционных картин, создаваемых многими парами когерентных источников.

стности полос до их практически полного размытия. Пусть расстояние между отверстиями ρ. Рассмотрим излучение в направлении угла φ (волновые вектора 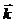 и
и 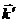 ). Разность хода волн Δ = ρsinφ. В случае малого угла φ можно заменить sinφ на φ, тогда Δ = ρφ. Соответствующая этой разности хода разность фаз лучей
). Разность хода волн Δ = ρsinφ. В случае малого угла φ можно заменить sinφ на φ, тогда Δ = ρφ. Соответствующая этой разности хода разность фаз лучей 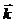 и
и 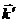
δ = kΔ = 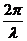 ρφ.
ρφ.
При разности фаз ≈π максимумы наложатся на минимумы, интерференционная картина будет размытой, неразличимой. (Заметим, что при малых ρ максимумы наложатся на максимумы, минимумы - на минимумы, картина будет контрастной).
Исходя из выше сказанного, приравняем 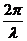 ρφ≈π. Максимальный угол φ в одну сторону φ =
ρφ≈π. Максимальный угол φ в одну сторону φ = 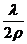 . Учитывая излучение от одной щели по обе стороны от нормали к щели (
. Учитывая излучение от одной щели по обе стороны от нормали к щели ( 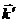 и
и 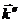 ), получим Δφ = 2φ = 2λ /2ρ = λ / ρ. Согласно данному в начале пункта определения радиуса когерентности, из последнего соотношения получаем радиус когерентности
), получим Δφ = 2φ = 2λ /2ρ = λ / ρ. Согласно данному в начале пункта определения радиуса когерентности, из последнего соотношения получаем радиус когерентности
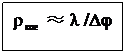 |
(32-3)
Соотношение (32-3) является ограничением размеров источника.
Пример. Имеется некоторый светящийся предмет размером d (рис. 32.2),
 |
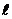 можно оценить как d≈
можно оценить как d≈ 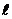 Δφ. Из соотношения (32-3) Δφ ≈λ / ρ, тогда d ≈
Δφ. Из соотношения (32-3) Δφ ≈λ / ρ, тогда d ≈ 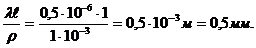 То есть, размеры предметы должны быть < 0,5 мм. Если размеры больше, то для получения интерференционной картины нужно ставить диафрагму.
То есть, размеры предметы должны быть < 0,5 мм. Если размеры больше, то для получения интерференционной картины нужно ставить диафрагму.
3. Оптическая длина пути. Расчет интерференционной картины о двух когерентных источников.
Произведение геометрической длины пути 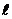 световой волны в среде на абсолютный показатель преломления n называется оптической длиной пути (ОДП) L. Для однородной среды L = n
световой волны в среде на абсолютный показатель преломления n называется оптической длиной пути (ОДП) L. Для однородной среды L = n 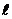 , а для неоднородной L =
, а для неоднородной L = 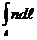 . Пусть некоторый источник света S испускает волны в двух направлениях
. Пусть некоторый источник света S испускает волны в двух направлениях
 | |||
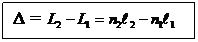 |
Величина называется оптической разностью хода
|
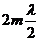 (целое число длин волн
(целое число длин волн 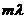 ), т. е.
), т. е. (32-4)
то колебания, возбужденные в данной точке экрана А обеими волнами будут проходить в одинаковой фазе и максимально усилят друг друга (условие (32-4) – условие min интерференции).
Если же на длине Δ укладывается нечетное число полуволн
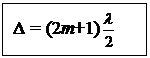 |
(m = 0, 1, 2…) (32-5)
то колебания будут происходить в противофазе, световые волны в данной точке максимально ослабят друг друга (условие (32-5) – условие min).