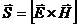Энергия и поток энергии электромагнитных волн. Вектор Пойнтинга.
Поскольку и электрическое и магнитное поля обладают определенной энергией, то электромагнитная волна имеет определенный запас энергии. Объемная плотность электрического поля 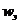 = ℰℰ
= ℰℰ 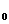
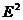 /2, магнитного поля
/2, магнитного поля 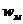 = μμ
= μμ 
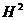 /2. Можно показать [ ], что вследствие равноценности электрического и магнитного полей
/2. Можно показать [ ], что вследствие равноценности электрического и магнитного полей 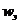 =
= 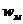 . То есть
. То есть
ℰℰ 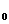
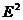 /2= μμ
/2= μμ 
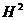 /2.
/2.
Извлекая, квадратный корень из обеих частей, получим


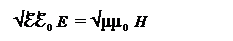
 (30-16)
(30-16)
 Существенно то, что электрическое и магнитное поля колеблются в одинаковых фазах. Они одновременно достигают максимума и минимума, но в двух взаимно перпендикулярных плоскостях.
Существенно то, что электрическое и магнитное поля колеблются в одинаковых фазах. Они одновременно достигают максимума и минимума, но в двух взаимно перпендикулярных плоскостях.
Плотность энергии электромагнитного поля складывается из составляющих
w = 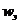 +
+ 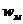 = ℰℰ
= ℰℰ 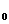
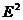 /2 + = μμ
/2 + = μμ 
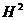 /2
/2
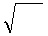 |
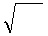
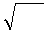
Представляя ℰℰ 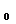 ∙
∙ 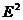 /2 как ℰℰ
/2 как ℰℰ 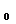 ∙
∙ 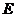 ∙ ℰℰ
∙ ℰℰ 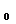 ∙
∙ 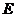 /2 и μμ
/2 и μμ  ∙
∙ 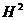 /2 как μμ
/2 как μμ  ∙
∙ 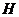 ∙
∙
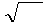 μμ
μμ  ∙
∙ 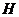 /2, получим
/2, получим
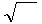
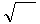
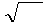
 w = ℰℰ
w = ℰℰ 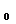 ∙
∙ 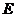 ∙ ℰℰ
∙ ℰℰ 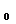 ∙
∙ 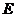 /2 + μμ
/2 + μμ  ∙
∙ 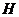 ∙ μμ
∙ μμ  ∙
∙ 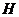 /2
/2
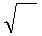

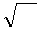
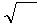 Умножим и разделим первое слагаемое на μμ
Умножим и разделим первое слагаемое на μμ  ∙
∙ 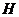 , а второе на ℰℰ
, а второе на ℰℰ 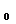 ∙
∙ 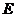
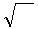
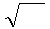
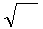
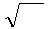 w = μμ
w = μμ  ∙
∙ 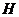 ℰℰ
ℰℰ 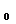 ∙
∙ 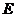 /2 ∙ ℰℰ
/2 ∙ ℰℰ 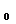 ∙
∙ 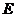
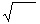

 / μμ
/ μμ  ∙
∙ 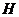
 + ℰℰ
+ ℰℰ 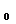 ∙
∙ 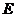 μμ
μμ 
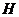 /2∙
/2∙
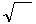
 ∙ μμ
∙ μμ  ∙
∙ 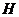 / ℰℰ
/ ℰℰ 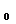 ∙
∙ 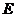
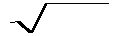 Учитывая равенство (30-16), производим необходимые сокращения и в результате получим
Учитывая равенство (30-16), производим необходимые сокращения и в результате получим
w = ℰ∙ℰ 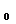 ∙μ∙μ
∙μ∙μ 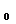 ∙
∙ 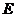 ∙
∙ 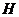
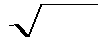 Поскольку 1/ ℰ∙μ∙ℰ
Поскольку 1/ ℰ∙μ∙ℰ 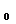 ∙μ
∙μ 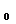 = u - скорость распространения электромагнитной волны (см. (30-15)), то w = 1/ u ∙
= u - скорость распространения электромагнитной волны (см. (30-15)), то w = 1/ u ∙ 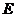
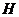 . Умножив найденное выражение для w на скорость волны u, получим модуль вектора плотности потока энергии S =w∙u =
. Умножив найденное выражение для w на скорость волны u, получим модуль вектора плотности потока энергии S =w∙u = 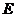 ∙
∙ 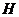 . Векторы
. Векторы 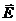 и
и 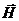 перпендикулярны и образуют с направлением распространения волны правовинтовую систему. Следовательно, вектор плотности потока электромагнитной энергии можно представить как векторное произведение
перпендикулярны и образуют с направлением распространения волны правовинтовую систему. Следовательно, вектор плотности потока электромагнитной энергии можно представить как векторное произведение 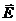 и
и 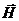 , так как направление вектора
, так как направление вектора 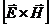 совпадает с направлением переноса энергии, а модуль этого вектора равен
совпадает с направлением переноса энергии, а модуль этого вектора равен 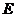
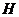 . Таким образом
. Таким образом
|
(30-17)
Вектор 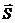 называется вектором Пойнтинга. (Или вектором Умова-Пойнтинга.) Общее представление о потоке энергии в пространстве впервые было введено русским ученым Умовым в 1874 г. Поэтому вектор потока энергии без конкретизации ее физической природы называется вектором Умова. Пойнтингом было получено выражение (30-17).)
называется вектором Пойнтинга. (Или вектором Умова-Пойнтинга.) Общее представление о потоке энергии в пространстве впервые было введено русским ученым Умовым в 1874 г. Поэтому вектор потока энергии без конкретизации ее физической природы называется вектором Умова. Пойнтингом было получено выражение (30-17).)
Физический смысл вектора Пойнтинга – плотность потока электромагнитной энергии, распространяющейся вместе с волной, то есть количество энергии, проходящей за единицу времени через единицу площади, расположенной перпендикулярно к направлению распространения волны (рис. 30.6).
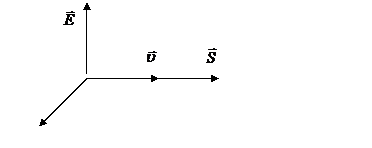
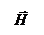
5. Изучение диполя. Диаграмма направленности.
Простейшим излучателем электромагнитных волн является электрический диполь, электрический момент которого изменяется во времени по гармоническому закону 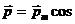 ωt, где
ωt, где 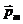 - амплитуда вектора
- амплитуда вектора 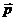 . Примером подобного диполя может служить система, состоящая из покоящегося заряда +Q и отрицательного заряда – Q, гармонически колеблющегося вдоль направления
. Примером подобного диполя может служить система, состоящая из покоящегося заряда +Q и отрицательного заряда – Q, гармонически колеблющегося вдоль направления 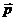 с частотой ω.
с частотой ω.
Задача об излучении диполя имеет в теории излучающих систем важное значение, так как всякую реальную излучающую систему (например, антенну) можно рассчитывать, рассматривая излучение диполя. Кроме того, многие вопросы взаимодействия излучения с веществом можно объяснить на основе классической теории, рассматривая атомы как системы зарядов, в которых электроны совершают гармонические колебания около их положения равновесия.
Характер электромагнитного поля диполя зависит от выбора рассматриваемой точки. Особый интерес представляет так называемая волновая зона диполя – точки пространства, отстоящие от диполя на расстоянии r, значительно превышающего длину волны (r>>λ), так как в ней картина электромагнитного поля диполя сильно упрощается. Это связано с тем, что в волновой зоне диполя практически остаются только «отпочковавшиеся» от диполя, свободно распространяющиеся поля, в то время как поля, колеблющиеся вместе с диполем и имеющие более сложную структуру, сосредоточены в области расстояний r<<λ. (Заметим, что в этой области справедливы те же формулы, что и для постоянных электрического и магнитного полей.)
В волновой зоне векторы 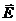 и
и  колеблются по закону cos(ωt –kr). Амплитуды этих векторов зависят от расстояния r до излучателя и угла ϑ между направлением радиуса-вектора и осью диполя и пропорциональны
колеблются по закону cos(ωt –kr). Амплитуды этих векторов зависят от расстояния r до излучателя и угла ϑ между направлением радиуса-вектора и осью диполя и пропорциональны 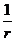 sinϑ. Отсюда следует, что интенсивность излучения диполя в волновой зоне
sinϑ. Отсюда следует, что интенсивность излучения диполя в волновой зоне 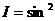 ϑ/
ϑ/ 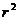 .
.
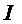 Зависимость от ϑ при заданном значении r, приводимая в полярных координатах, называется диаграммой направленности излучения диполя (см. рис. 30.7).
Зависимость от ϑ при заданном значении r, приводимая в полярных координатах, называется диаграммой направленности излучения диполя (см. рис. 30.7).

Вопросы для самоконтроля.
1. В чем заключается максвелловская трактовка явления электромагнитной индукции?
2. Что называется током смещения?
3. Напишите систему уравнений Максвелла в интегральной и дифференциальной формах. В чем состоит физический смысл каждого уравнения?
4. Напишите волновые уравнения для электромагнитного поля и их решения.
5. Перечислите Основные свойства электромагнитных волн.
6. Что называется вектором Пойнтинга? Каков его физический смысл?
7. нарисуйте диаграмму направленности излучения диполя.
ОПТИКА
Лекция № 31