Упругие свойства твердых тел.
ε׀׀=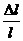 
– относительное удлинение;
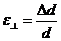– относительное поперечное сжатие;
( 
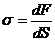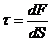) – нормальное (тангенциальное) механическое напряжение;
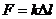; ε׀׀= 
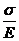– закон Гука;
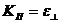/ ε׀׀ – коэффициент Пуассона;
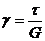– закон Гука для деформации сдвига; где γ – деформация сдвига (угол сдвига);
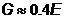– связь между модулем Юнга и модулем сдвига.
| Вещество | Плот-ность, кг/м3 | Модуль Юнга, Е.10-10 Па | Предел прочности, σпр.10-8 Па |
| Алюминий | 6.9 | 1.1 | |
| Железо | 19.6 | ||
| Латунь | - | - | |
| Медь | 11.8 | 2.4 | |
| Платина | - | - | |
| Сталь | 21.6 | 7.85 | |
| Цинк | - | - |
137. Железная проволока длиной 5 м висит вертикально. На сколько изменится объем проволоки, если к ней привязать гирю массой 10 кг? Коэффициент Пуассона для железа принять равным 0.3.
138. Однородный стальной стержень длиной 2 м равномерно вращается вокруг вертикальной оси, проходящей через один из его концов. При какой угловой скорости вращения стержень разорвется?
139. Найти момент пары сил, необходимый для закручивания проволоки длиной 10 см и радиусом 0.1 мм на угол 10 минут. Модуль сдвига материала проволоки равен 5.109 Па.
140. Вычислить момент сил, которые вызывают закручивание стальной трубы длиной 3 м на угол 20 вокруг ее оси, если внутренний и внешний диаметры трубы равны 30 мм и 50 мм соответственно.
141. Определить работу растяжения стальной проволоки длиной 2 м и радиусом 3 мм под действием груза 200 кг.
142. Стальная проволока длиной 1 м закреплена одним концом так, что может совершать колебания в вертикальной плоскости. К свободному концу проволоки прикрепили груз массой 50 кг. Проволоку с грузом отклоняют на высоту подвеса и отпускают. Определить абсолютное удлинение проволоки в нижней точке траектории при движении груза. Сечение проволоки 0.8 мм2, массой проволоки пренебречь.
143. Стальная проволока диаметром 1 мм имеет длину 5 м, когда на ней висит груз весом 196 Н. На сколько удлинится проволока, если вес груза увеличить на 98 Н?
144. При растяжении медной проволоки, поперечное сечение которой равно 1.5 мм2, начало остаточной деформации наблюдалось при нагрузке 4.5 кг. Каков предел упругости материала проволоки?
145. Каким должен быть предельный диаметр стального троса, чтобы он выдержал нагрузку 1 т?
146. Найти длину медной проволоки, которая, будучи подвешена вертикально, начинает рваться под действием собственного веса.
147. Имеется резиновый шланг длиной 50 см и внутренним диаметром 1 см. Шланг растянули до длины 60 см. Найти внутренний диаметр натянутого шланга, если для резины коэффициент Пуассона равен 0.5.
148. Найти относительное изменение плотности цилиндрического медного стержня при сжатии его давлением 108 Па. Коэффициент Пуассона для меди принять равным 0.34.
149. Найти значение коэффициента Пуассона, при котором объем проволоки при растяжении не меняется.
150. К стальной проволоке радиусом 1 мм подвешен груз 100 кг. На какой наибольший угол можно отклонить проволоку с грузом, чтобы она не разорвалась при прохождении этим грузом положения равновесия?
151. К железной проволоке длиной 50 см и диаметром 1 мм привязана гиря массой 1 кг. С какой угловой скоростью можно равномерно вращать в вертикальной плоскости такую проволоку с грузом, чтобы она не разорвалась?
152. Установить связь между крутящим моментом сил и углом закручивания для трубы длиной l, у которой толщина стенок Δr значительно меньше радиуса трубы R. Модуль сдвига равен G.
153. Установить связь между крутящим моментом сил и углом закручивания для сплошного стержня круглого сечения радиусом R и длиной l. Модуль сдвига равен G.