Обмотки якоря машин постоянного тока

В процессе развития машин постоянного тока не сразу пришли к современному типу якоря – цилиндрическому. На первом этапе развития якорь был кольцевым. Но в связи с малым использованием меди в этих якорях перешли к барабанным. В пазах железа якоря укладывается обмотка. Под обмоткой понимается вся совокупность проводников, которые закладываются в пазы и которые соединяются в строго определенном порядке. Число которых достигает нескольких сотен и даже тысяч.

Основные требования предъявляемые к обмотке

1. Обмотка должна быть замкнута сама на себя, т. е. если начали обход обмотки от какой-то пластины, то после обхода должны прийти к этой же пластине.

2. Отдельные проводники обмотки соединены таким образом, при котором обеспечивается наибольшая ЭДС.

3. Сумма ЭДС по контуру обмотки должна быть равна нулю, (рис. 6). Если по 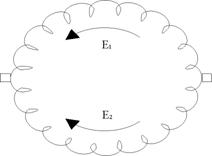контуру обмотки сумма ЭДС не равна нулю, то появляются уравнительные токи.

Для того, чтобы представить себе обмотку, пользуются методом развертки.

Основным элементом обмотки является секция. Секцией называется часть обмотки, которая заключена между двумя коллекторными пластинами.

рис. 6 В машинах постоянного тока используются следующие типы обмоток:

1. Простая петлевая обмотка

2. Простая волновая обмотка

3. Сложно-петлевая обмотка

4. Сложно-волновая обмотка

5. Смешанная (лягушечная) обмотка

Простая петлевая обмотка

Для того, чтобы выполнить обмотку в развернутом виде необходимо рассчитать четыре шага; (рис. 7)

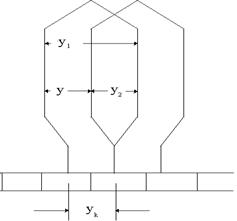
1. Первый шаг – шаг по коллектору –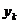

Шаг по коллектору – расстояние между осями коллекторных пластин концов секции.

Шаг по коллектору измеряется числом коллекторных делений. В простой петлевой обмотке шаг по коллектору 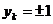. В практике используется правоходовая (знак ).

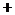2. Второй шаг – первый частичный шаг – это расстояние между начальной и конечной активными сторонами секции – .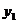

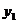- измеряется числом элементарных пазов

рис. 7 расположенных между активными сторонами.

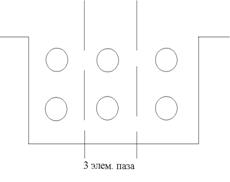Элементарным пазом называется такой паз, в котором расположены две активные стороны. На рис. 8 представлен один реальный паз с тремя элементарными.

3. Третий шаг – второй частичный шаг –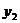

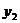- это расстояние между конечной стороной одной секции и начальной стороной другой секции и измеряется элементарными пазами.

4. Четвертый шаг - 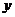- результирующий шаг – это расстояние между соответствующими

рис. 8 сторонами двух секций идущими одна за другой.

Этими основными шагами и характеризуется обмотка. В любой обмотке активные стороны секции необходимо расположить так, чтобы в ней индуктировалась наибольшая ЭДС.

Максимальная ЭДС будет тогда, когда активные стороны проходят через центр полюсов, рис. 9.

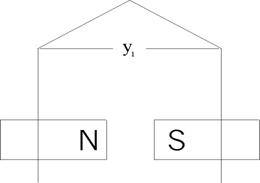Первый частичный шаг 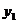определяется по формуле 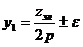, где

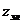- число элементарных пазов

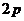- число полюсов

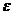- долевая величина, которая обеспечивает целое число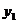

Если 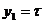, то это обмотка с полным шагом, если 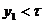, то с укороченным шагом.

рис. 9

Определим результирующий шаг - .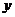

Обозначим:

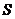- число секций

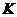- число коллекторных пластин

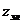- число элементарных пазов

При элементарных пазах число секций равно числу коллекторных пластин. Кроме того, число элементарных пазов равно числу секций.

Тогда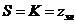

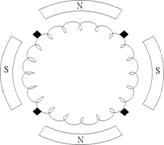Так как отступление секций по коллектору строго соответствует отступлению секций по элементарным пазам, следовательно .

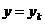Второй частичный шаг – .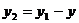

В простой петлевой обмотке число параллельных ветвей равно числу полюсов 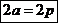(рис. 10).

Число параллельных ветвей определяют область применения машины.

Простая петлевая обмотка применяется для машин средней мощности при номинальном напряжении.

рис. 10

Простая волновая обмотка

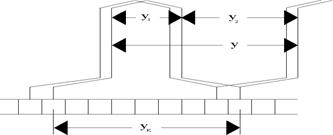
На рисунке представлены секции волновой обмотки с указанием основных шагов, (рис. 11).

Определение основных шагов: первый частичный шаг 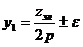рис. 11

При обходе якоря, каждая секция волновой обмотки занимает по окружности якоря двойное полюсное деление. Если машина имеет - 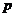- пар полюсов, то при обходе окружности якоря мы уложим 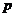секций. Причем последняя секция либо не дойдет на исходную коллекторную пластину (на одну раньше), либо перейдет исходную коллекторную пластину, т.е. 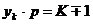(в практике используется левоходовая обмотка со знаком минус). Откуда шаг по коллектору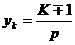

Так как отступление секций по коллектору строго соответствует отступлению секций по элементарным пазам, отсюда , .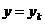

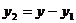В простой волновой обмотке число параллельных ветвей равно ,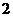

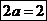
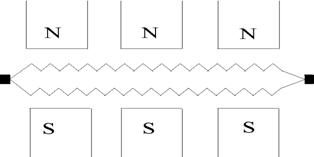Условно простую волновую обмотку можно представить на рис. 12. Из рисунка видно, что чем больше число полюсов, тем выше напряжение на якоре. Поэтому простая волновая обмотка используется для машин малой мощности но при повышенном напряжении. Число установленных щеток равно числу полюсов.

рис. 12

Сложные обмотки

Сложные обмотки состоят из простых обмоток и бывают сложно-петлевые и сложно-волновые.

Сложно-петлевая обмотка

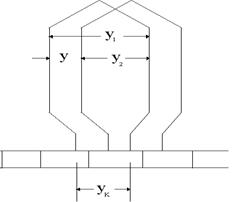сложная обмотка отличается от простой обмотки шагом по коллектору, рис. 13.

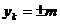(обычно 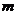не более ).

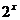Результирующий шаг .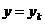

Шаг 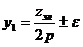, а .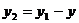

Сложно-петлевые обмотки могут быть однократнозамкнутые и двухкратнозамкнутые (двух ходвые).

Пусть 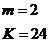намотку с 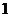пластины, т. е. 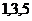и рис. 13 т.д. получим одну обмотку. Вторая обмотка будет

соединена со всеми четными пластинами ( 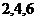и т. д.). В этом случае получим две независимые обмотки (двухкратнозамкнутую обмотку).

Если 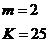при нечетном числе 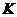при намотке обойдем секции соединенные с нечетными пластинами, а затем обмотку соединенную с четными пластинами. В этом случае получим двух ходовую однократнозамкнутную обмотку. Эта обмотка чаще используется на практике.

В сложно-петлевой обмотке число параллельных ветвей 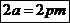, т. е. можно увеличить число параллельных ветвей не изменяя число полюсов. Эти обмотки применяются для токов большой величины, так как в них число параллельных ветвей велико. Поэтому сложно-петлевые обмотки применяются для машин большой мощности номинальном напряжении.

Сложно-волновые обмотки

Сложно-волновые обмотки состоят из простых волновых обмоток. Они могут быть однократнозамкнутые (двух ходовые) и двухкратнозамкнутыми. Основные шаги определяются:

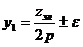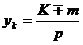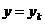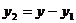, , , где .

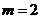Число параллельных ветвей в сложно-волновой обмотке .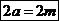

Сложно-волновая обмотка применяется для машин средней мощности с повышенным напряжением.

На практике намотку ведут по реальному шагу 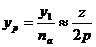, где: - число элементарных пазов, 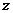- число реальных пазов.

Симметрия обмоток

Обмотка состоит из параллельных ветвей, ветви обмотки совершенно одинаковы – симметричные. В симметричной обмотке в параллельных ветвях наводятся одинаковые ЭДС и протекают одинаковые токи, но для этого необходимо выполнить ряд условий.

Условия симметрии обмотки :

На каждую пару параллельных ветвей ( 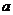) должно приходиться одинаковое число секции ( 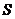), реальных пазов ( 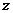), и полюсов ( ).

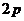1.

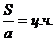
2.

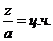
3.

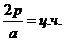
В практике этих условий недостаточно. Приходится использовать уравнительные соединения первого рода и уравнительные соединения второго рода.

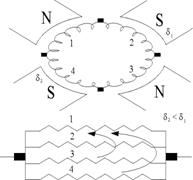а) Уравнительные соединения первого рода.

Уравнительные соединения первого рода применяются для выравнивания магнитной несимметрии и используются только для петлевых обмоток.

В петлевых обмотках, каждая ветвь расположена под своим полюсом. Но поток может быть неодинаков из-за неравномерного зазора (просел подшипник, неправильная сборка машины), что приводит к магнитной несимметрии. А при магнитной несимметрии машина работает в не нормальных условиях: перегрузка отдельных ветвей, недогрузка других. (см. рис. 14).

В обмотках при нормальных условиях имеются точки с одинаковыми потенциалами и если их соединить уравнителями, то тока в них не будет. При нарушении магнитной симметрии в параллельных ветвях наводятся различные ЭДС, что приводит к появлению уравнительных токов внутри обмотки. Этот уравнительный ток ликвидирует магнитную

несимметрию. По обмотке и уравнительным соединениям протекает переменный ток. Создается многофазная системная, которая создает вращающееся поле. Это поле вращается с такой же скоростью что и якорь, но в противоположную сторону, т. е. оно неподвижно относительно полюсов. Это поле усиливает поток под полюсами где оно ослаблено и ослабляет поток, где поле большое. Таким образом происходит выравнивание магнитной несимметрии.

Способы выполнения уравнительных соединений первого рода

Уравнительные соединения первого рода выполняются либо со стороны коллектора, либо с противоположной стороны на изолирующих кольцах.

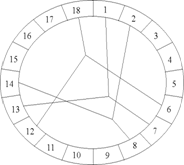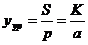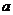В обмотке имеются точки с одинаковыми потенциалами. Эти точки должны быть соединены. Промежуток между равнопотенциальными точками одинаков. Шаг уравнительного соединения определяется по формуле , где - число пар параллельных ветвей.

Число 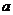определяет число точек соединенных в один узел.

Рис. 15

Пример: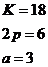

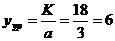
То одинаковый потенциал имеют следующие точки.

В примере уравнительные соединения выполнены

со стороны коллектора. Если они выполнены с -----------

противоположной стороны, то точки одинакового ,рис. 15

потенциала собираются на изолирующих кольцах.

Однако при большом количестве коллекторных пластин 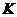полное число уравнительных соединений не выполняется (только в специальных машинах). Обычно делают на один реальный паз один уравнитель.

Уравнители выполняются проводом сечением 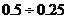от сечения провода обмотки. Уравнительные соединения первого рода применяются только в петлевых обмотках, а в волновых уравнительные соединения первого рода не нужны, так как число пар параллельных ветвей 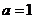(одна равнопотенциальная точка). Кроме того, параллельные ветви волновой обмотки последовательно проходят через все полюса, то магнитная несимметрия одинаково сказывается на этих параллельных ветвях.

б) Уравнительные соединения второго рода

Уравнительные соединения второго рода применяются только для сложных обмоток: сложно-петлевых и сложно-волновых.

Уравнительные соединения второго рода служат для выравнивания неравномерного распределения потенциала вдоль коллектора.

В сложных все происходит по разному, простые обмотки лежат рядом и на коллекторе перекрываются одной щеткой. Если сопротивления между коллекторными пластинами и щеткой равны, то изменение потенциала сказывается одинаково на обеих обмотках.

Однако переходные сопротивления (коллектор-щетка) простых обмоток не равны и распределения токов в этих обмотках будут неравномерными. А это приведет к неравномерному распределению потенциала на коллекторе. Для выравнивания неравномерного потенциала на коллекторе выполняют уравнительные соединения второго рода, рис. 16.

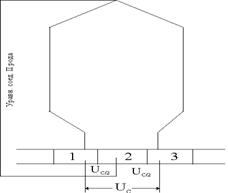Уравнительные соединения второго рода должны соединять коллекторные пластины простых обмоток, имеющих при нормальных условиях одинаковые потенциалы. Шаг уравнительного соединения .

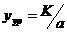Сложно-петлевые обмотки имеют уравнительные соединения первого и второго рода.

Сложно-волновые обмотки имеют только уравнительные соединения второго рода.

рис. 16