Политропный процесс, его частные случаи: изобарный, изотермический, адиабатный, изохорный.

Процесс, в ко тором теплоемкость остается постоянной, называется политропным.

Исходя из первого начала термодина мики при условии постоянства теплоемко сти (C = const) можно вывести уравнение политропы:

pVⁿ = const, (55.9) где n=(C-С_р)/(С-C_v) — показатель политропы. Очевидно, что при С = 0, n= из (55.9) получается уравнение адиабаты; при С=, n=1 —уравнение изотермы; при С=С_Р, n = 0 — уравнение изобары, при С = С_v, n=± —уравнение изохоры.

Среди равновесных процессов, происходя щих с термодинамическими системами, выделяются изопроцессы,при которых один из основных параметров состояния сохраняется постоянным.

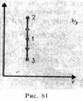
Изохорный процесс(V = const). Диаг рамма этого процесса (изохора)в коорди натах р, V изображается прямой, парал лельной оси ординат (рис. 81), где процесс 1—2 есть изохорное нагревание, а 1—3 — изохорное охлаждение. При изохорном процессе газ не совершает работы над внешними телами, т. е.

A=pdV = 0.

Как уже указывалось в § 53, из первого начала термодинамики (Q=dU+A) для изохорного процесса следует, что вся теп лота, сообщаемая газу, идет на увеличе ние его внутренней энергии:

Q =dU

Согласно формуле (53.4), dU_m = C_vdT.

Тогда для произвольной массы газа по лучим

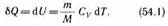
Изобарный процесс(р=const). Диаграмма этого процесса (изобара)в координатах р, V изображается прямой, парал лельной оси V

. При изобарном процессе работа газа при расширении объема от V₁до V₂ равна

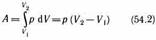
и определяется площадью прямоугольни ка, выполненного в цвете на рис. 82. Если использовать уравнение Клапейро на — Менделеева для выбранных нами двух состояний, то

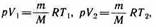
откуда

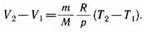
Тогда выражение (54.2) для работы изо барного расширения примет вид

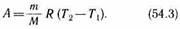
Из этого выражения вытекает физический смысл молярной газовой постоянной R: если T₂-T₁=1К, то для 1 моля газа R=А, т. е. R численно равна работе изо барного расширения 1 моля идеального газа при нагревании его на 1 К.

В изобарном процессе при сообщении газу массой от количества теплоты

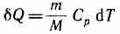
его внутренняя энергия возрастает на ве личину (согласно формуле (53.4))

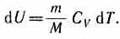
При этом газ совершит работу, определяе мую выражением (54.3).

Изотермический процесс(T=const). Изотермиче ский процесс описывается законом Бой ля — Мариотта:

pV=const.

Диаграмма этого процесса (изотерма)в координатах р, V представляет собой гиперболу, расположенную на диаграмме тем выше, чем выше темпе ратура, при которой происходил процесс. Найдем работу изотермического расшире ния газа:

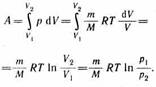
Так как при T=const внутренняя энергия идеального газа не изменяется:

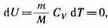
то из первого начала термодинамики (Q =dU+A) следует, что для изотермиче ского процесса

Q=A,

т. е. все количество теплоты, сообщаемое газу, расходуется на совершение им рабо ты против внешних сил:

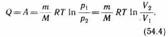
Следовательно, для того чтобы при рабо те расширения температура не уменьша лась, к газу в течение изотермического процесса необходимо подводить количест во теплоты, эквивалентное внешней работе расширения.