Дифракция света.принцип Гюйгенса. Принцип Гюйгенса-Френеля.

Дифракцией света называется явление отклонения света от прямолинейного направления распространения при прохождении вблизи препятствий

Согласно принципу Гюйгенса каждая точка среды, до которой дошло возмущение, сама становится источником вторичных волн.
Для механических волн принцип Гюйгенса имеет наглядное истолкование: частицы среды, до которых доходят колебания, в свою очередь, колеблясь, приводят в движение соседние частицы среды, с которыми они взаимодействуют.

Принцип Гюйгенса — Френеля формулируется следующим образом:
Каждый элемент волнового фронта можно рассматривать, как центр вторичного возмущения, порождающего вторичные сферические волны, а результирующее световое поле в каждой точке пространства будет определяться интерференцией этих волн.

33.метод зон Френеля.площади зон. радиусы зон. Метод векторных диаграмм.

Френель предложил оригинальный метод разбиения волновой поверхности S на зоны, позволивший сильно упростить решение задач (метод зон Френеля).

Границей первой (центральной) зоны служат точки поверхности S, находящиеся на расстоянии 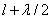от точки M (рис. 9.2). Точки сферы S, находящиеся на расстояниях 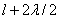, , 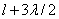и т.д. от точки M, образуют 2, 3 и т.д. зоны Френеля.

Колебания, возбуждаемые в точке M между двумя соседними зонами, противоположны по фазе, так как разность хода от этих зон до точки M .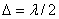

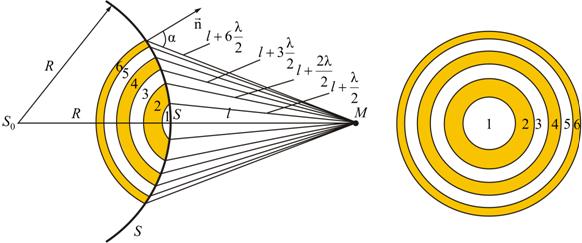
Рис. 9.2

Поэтому при сложении этих колебаний, они должны взаимно ослаблять друг друга:

,

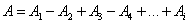(9.2.2)

где A – амплитуда результирующего колебания, 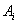– амплитуда колебаний, возбуждаемая i-й зоной Френеля.

Величина 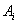зависит от площади 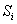зоны и угла 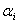между нормалью к поверхности и прямой, направленной в точку M.

Площадь одной зоны

.

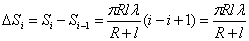Отсюда видно, что площадь зоны Френеля не зависит от номера зоны i. Это значит, что при не слишком больших i площади соседних зон одинаковы.

В то же время с увеличением номера зоны возрастает угол 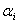и, следовательно, уменьшается интенсивность излучения зоны в направлении точки M, т.е. уменьшается амплитуда 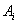. Она уменьшается также из-за увеличения расстояния до точки M:

.

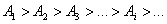Общее число зон Френеля, умещающихся на части сферы, обращенной в сторону точки M, очень велико: при 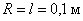, , 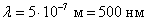число зон 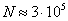, а радиус первой зоны .

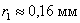Отсюда следует, что углы между нормалью к зоне и направлением на точку M у соседних зон примерно равны, т.е. что амплитуды волн, приходящих в точку Mот соседних зон,примерно равны.

Световая волна распространяется прямолинейно. Фазы колебаний, возбуждаемые соседними зонами, отличаются на π. Поэтому в качестве допустимого приближения можно считать, что амплитуда колебания 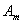от некоторой m-й зоны равна среднему арифметическому от амплитуд примыкающих к ней зон, т.е.

.

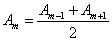Тогда выражение (9.2.1) можно записать в виде

.

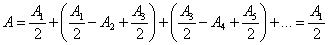(9.2.2)

Так как площади соседних зон одинаковы, то выражения в скобках равны нулю, значит результирующая амплитуда .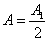

Интенсивность излучения .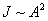

Таким образом, результирующая амплитуда, создаваемая в некоторой точке M всей сферической поверхностью, равна половине амплитуды, создаваемой одной лишь центральной зоной, а интенсивность .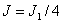

Так как радиус центральной зоны мал ( 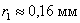), следовательно, можно считать, что свет от точки P до точки M распространяется прямолинейно.

Если на пути волны поставить непрозрачный экран с отверстием, оставляющим открытой только центральную зону Френеля, то амплитуда в точке M будет равна 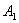. Соответственно, интенсивность в точке M будет в 4 раза больше, чем при отсутствии экрана (т.к. 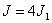). Интенсивность света увеличивается, если закрыть все четные зоны.

Таким образом, принцип Гюйгенса–Френеля позволяет объяснить прямолинейное распространение света в однородной среде.

Правомерность деления волнового фронта на зоны Френеля подтверждена экспериментально. Для этого используются зонные пластинки – система чередующихся прозрачных и непрозрачных колец.

Опыт подтверждает, что с помощью зонных пластинок можно увеличить освещенность в точке М, подобно собирающей линзе.

Векторная диаграмма — графическое изображение меняющихся по закону синуса (косинуса) величин и соотношений между ними при помощи направленных отрезков — векторов. Векторные диаграммы широко применяются в электротехнике, акустике, оптике, теории колебаний и так далее.

Метод векторной диаграммы состоит в следующем: переменные токи, напряжения и ЭДС изображаются в виде векторов, длина которых соответствует амплитуде этих величин, вектора изображаются неподвижными, но подразумевается, что они вращаются против часовой стрелки с частотой 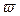. При таком равномерном вращении вектора 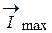его проекция на вертикальную ось будет изменяться во времени по законусинуса и, если значение проекции дляразных моментов времени перенести на временную диаграмму, то линия, соединяющая концы отрезков, будет синусоидой

34.дифракция френеля на круглом отверстии ,на круглом диске

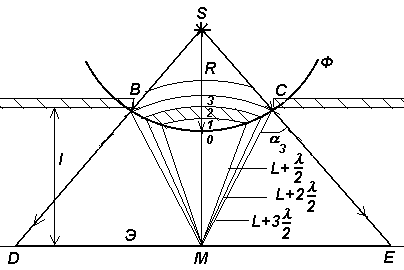Рис.2

Сферическая волна, распространяющаяся из точечного источника монохроматического света S, встречает на своем пути экран с круглым отверстием, диаметр которогоd=BC. Пусть Ф - фронт волны, который является частью поверхности сферы. Разобьем поверхность фронта на зоны Френеля (см. рис.2) так, что волны от соседних зон приходят в точку наблюдения Мв противофазе. Тогда амплитуда результирующей волны в точке М

А=А₁-А₂+А₃-А₄+- 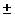А_m , (1)

где А_i - амплитуда волны, пришедшей от i-ой зоны Френеля. Перед А_m берется знак плюс, если m - нечетное, и минус, если m - четное.

Величина А_i зависит от площади s_i i-той зоны и угла a_i между внешней нормалью к поверхности зоны в какой-либо точке и прямой, направленной из этой точки в точку М (см. рис.2, где в частности показан угол a₃).

Можно показать, что все зоны Френеля примерно равновелики по площади. Увеличение же углаa_i с ростом номера зоны приводит к уменьшению амплитуды А_i. Она уменьшается с ростом i также и вследствие увеличения расстояния от зоны до точки М. Таким образом, А₁>А₂>->A_m . При большом числе зон можно приближенно считать, чтоА_i=(A_i-1+A_i+1)/2. (2)

Перепишем теперь (1) в виде

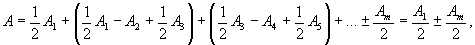(3)

так как согласно (2) все выражения, стоящие в скобках, равны нулю.

Можно показать, что общее число m зон Френеля, обращенное к точке М,

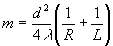, (4)

где d=BC - диаметр отверстия, R=SO, L=OM (см. рис.2), l- длина волны.

Если d=1 см, R=L=10 см и l=500 нм, то m=1000.

В этом случае А_m<<A₁ и слагаемым 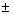А_m/2 в (3) можно пренебречь. Тогда согласно (3)

А=А₁/2. (5)

Таким образом, амплитуда результирующей волны в точке Мопределяется как бы действием только половины центральной зоны Френеля. Ее диаметр d, как следует из (4) при m=1, R=L=10 см иl=500 нм, равен 0,32 мм.

Следовательно, распространение света от S к М происходит так, будто пучок света распространяется внутри очень узкого канала вдоль SM, т.е. прямолинейно.

В этом случае круговое пятно диаметром ED (см. рис.2) равномерно освещено и вне его наблюдается тень. Следовательно, дифракционная картина отсутствует, когда диаметр отверстияBC=d>>l.

При уменьшении диаметра отверстия до величины d 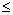1мм число зон согласно (4) уменьшается иА_m становится сравнимым с А_1, и поэтому пренебречь слагаемым 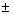А_m/2 в (3) нельзя.

При нечетном числе зон согласно (3)

А=А₁/2 +А_m/2(6)

и в точке Мнаблюдается максимум (светлое пятно).

При четном числе зон

А=А₁/2 -А_m/2 (7)

и в точке М будет наблюдаться минимум (темное пятно). Этот факт особенно наглядно противоречит закону прямолинейного распространения света.

Очевидно, что максимум и минимум будут тем сильнее отличаться друг от друга, чем ближе значение А_m к А₁, т.е. когда число зон m мало (m 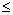10). Расчет амплитуды в других точках экрана более сложен. Можно показать, что дифракционная картина вблизи точки М имеет вид чередующихся темных и светлых колец с центрами в точке М. По мере удаления от точки Минтенсивность максимумов света убывает.

Если на пути световой волны в плоскости отверстия поставить зонную пластинку, которая перекрывала бы все четные зоны, то А=А₁+А₃+А₅+- и интенсивность I=A² в точке М резко возрастает. Еще большего эффекта можно достичь, не перекрывая четные зоны, а изменяя фазу их колебаний на p, тогда А=А₁+А₂+А₃+-Такая пластинка называется фазовой зонной пластинкой, и использование ее позволяет получить дополнительное увеличение интенсивности в 4 раза.

Опыт подтверждает эти выводы: зонная пластинка увеличивает интенсивность в точке М, действуя подобно собирающей линзе.