Колебания. Свободные, вынужденные, автоколебания, параметрические колебания.

Ответы по физике экзамен

Колебания. Свободные, вынужденные, автоколебания, параметрические колебания.

Колеба́ния — повторяющийся в той или иной степени во времени процесс изменения состояний системы около точки равновесия.

Свободные (или собственные) — это колебания в системе под действием внутренних сил после того, как система выведена из состояния равновесия (в реальных условиях свободные колебания всегда затухающие). Простейшими примерами свободных колебаний являются колебания груза, прикреплённого к пружине, или груза, подвешенного на нити.

Вынужденные — колебания, протекающие в системе под влиянием внешнего периодического воздействия. Примеры: листья на деревьях, поднятие и опускание руки. При вынужденных колебаниях может возникнуть явление резонанса: резкое возрастание амплитуды колебаний при совпадении собственной частоты осциллятора и частоты внешнего воздействия.

Автоколебания — колебания, при которых система имеет запас потенциальной энергии, расходующейся на совершение колебаний (пример такой системы — механические часы). Характерным отличием автоколебаний от вынужденных колебаний является то, что их амплитуда определяется свойствами самой системы, а не начальными условиями.

Параметрические — колебания, возникающие при изменении какого-либо параметра колебательной системы в результате внешнего воздействия.

2)Дифференциальное уравнение гармонических колебаний и его решение.

Гармоническая функция синус или косинус в зависимости от начальной фазы.

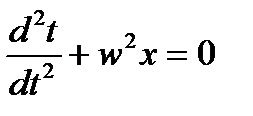
3)Гармонические колебания. Основные параметры гармонических колебаний. Скорость и ускорение при гармоническое колебательном движении.

Гармонические колебания – это колебания с постоянной амплитудой происходящие по закону синуса или косинуса.

Параметры гармонических колебаний. Постоянные величины А, Т, f, входящие в уравнение Acos( 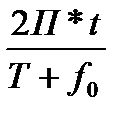)называются параметрами колебания. Рассмотрим их физический смысл.

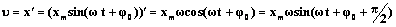
Из ур-я следует, что в случае, если соs(2p·t/Т + f) = ± 1, то значение модуля x максимально, т.е. |x| = xmax = A

Скорость – это производная от координаты по времени

Скорость при гармоническом колебательном движении также изменяется по гармоническому закону, но колебания скорости опережают колебания смещения по фазе на p/2.

Vmax=XmaxW:максимальная скорость колебательного движения(амплитуда колебаний скорости)

Ускорение – это производная от скорости по времени: a=V'=(x)'=x''(вторая производная)

Ускорение изменяется по гармоническому закону.

Amax=XmaxW^2:Макс ускорение

A=-amaxsin(wt+ф0):ускорение

Образование стоячей волны. Принцип суперпозиции волн. Когерентные волны.

Стоя́чая волна́ — явление интерференции волн, распространяющихся в противоположных направлениях, при котором перенос энергии ослаблен или отсутствует.

Стоячая волна (электромагнитная) — периодическое изменение амплитуды напряженности электрического и магнитного полей вдоль направления распространения, вызванное интерференцией падающей и отраженной волн.

Принцип суперпозиции (наложения) волн: при распространении в среде нескольких волн каждая из них распространяется так, как будто другие волны отсутствуют, а результирующее смещение частицы среды в любой момент времени равно геометрической сумме смещений, которые получают частицы каждой волны.

Интерференция волн – наложение двух (или нескольких) когерентных волн, в результате чего происходит усиление или ослабление результирующей волны в зависимости от соотношения между фазами этих волн.

Когерентными называются волны одного направления одинаковой частоты и постоянной разности фаз.

Кольца Ньютона

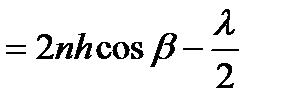
• Кольца Ньютона, являющиеся классическим примером полос равной толщины, наблюдаются при отражении света от воздушного зазора, образованного плоскопараллельной пластинкой и соприкасающейся с ней плосковыпуклой линзой с большим радиусом кривизны.

• Параллельный пучок света падает нормально на плоскую поверхность линзы и частично отражается от верхней и нижней поверхностей воздушного зазора между линзой и пластинкой. При наложении отраженных лучей возникают полосы равной толщины, при нормальном падения света имеющие вид концентрических окружностей.

31.интерферометр Майкельсона. Интерферометр Жамена. <<просветления оптики>>

Монохроматический свет от источника S падает под углом 45° на плоскопараллельную пластинку P1. Сторона пластинки, удаленная от S, посеребренная и полупрозрачная, разделяет луч на две части: луч 1 (отражается от посеребренного слоя) в луч 2 (проходит через него). Луч 1 отражается от зеркала M1 и, возвращаясь обратно, вновь проходит через пластинку P1 (луч 1'). Луч 2 идет к зеркалу М2, отражается от него, возвращается обратно и отражается от пластинки Р1 (луч 2'). Так как первый из лучей проходит сквозь пластинку Р1 дважды, то для компенсации возникающей разности хода на пути второго луча ставится пластинка Р2 (точно такая же, как и Р1, только не покрытая слоем серебра).

• Лучи 1' и 2' когерентны; следовательно, будет наблюдаться интерференция, результат которой зависит от оптической разности хода луча 1 от точкиО до зеркала М1 и луча 2 от точки О до зеркала M2. При перемещении одного из зеркал на расстояние l0/4 разность хода обоих лучей увеличится на l0/2 и произойдет смена освещенности зрительного поля. Следовательно, по незначительному смещению интерференционной картины можно судить о малом перемещении одного из зеркал и использовать интерферометр Майкельсона для точного (порядка 10–7 м) измерения длин (измерения длины тел, длины волны света, изменения длины тела при изменении температуры (интерференционный дилатометр)).

Интерферометр Жамена

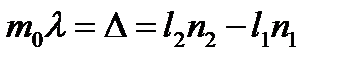
1. Измерение
   длин волн
2. Измерение
   показателей преломления
3. Контроль
   качества обработки поверхностей

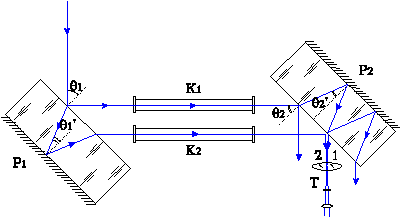
1.Пучок света S после отражения от передней и задней поверхностей пластины P₁ разделяется на два пучка S₁ и S₂

2.Пройдя через кюветы K₁ и K₂, пучки, отразившиеся от поверхностей пластины P₂, попадают в зрительную трубу T, где интерферируют, образуя полосы равного наклона

3.Если одна из кювет наполнена веществом с показателем преломления n₁, а другая с n₂, то по смещению интерференционной картины на число полос m
по сравнению со случаем, когда обе кюветы наполнены одним и тем же веществом, можно найти неизвестный n

толщину пленки
подбирают таким образом, чтобы для отраженного света выполнялось условие интерференционного минимума

для длин волн средней части спектра (λз~555 нм)

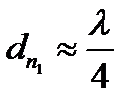
Ответы по физике экзамен

Колебания. Свободные, вынужденные, автоколебания, параметрические колебания.

Колеба́ния — повторяющийся в той или иной степени во времени процесс изменения состояний системы около точки равновесия.

Свободные (или собственные) — это колебания в системе под действием внутренних сил после того, как система выведена из состояния равновесия (в реальных условиях свободные колебания всегда затухающие). Простейшими примерами свободных колебаний являются колебания груза, прикреплённого к пружине, или груза, подвешенного на нити.

Вынужденные — колебания, протекающие в системе под влиянием внешнего периодического воздействия. Примеры: листья на деревьях, поднятие и опускание руки. При вынужденных колебаниях может возникнуть явление резонанса: резкое возрастание амплитуды колебаний при совпадении собственной частоты осциллятора и частоты внешнего воздействия.

Автоколебания — колебания, при которых система имеет запас потенциальной энергии, расходующейся на совершение колебаний (пример такой системы — механические часы). Характерным отличием автоколебаний от вынужденных колебаний является то, что их амплитуда определяется свойствами самой системы, а не начальными условиями.

Параметрические — колебания, возникающие при изменении какого-либо параметра колебательной системы в результате внешнего воздействия.

2)Дифференциальное уравнение гармонических колебаний и его решение.

Гармоническая функция синус или косинус в зависимости от начальной фазы.

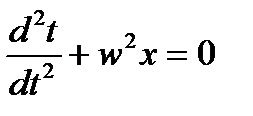
3)Гармонические колебания. Основные параметры гармонических колебаний. Скорость и ускорение при гармоническое колебательном движении.

Гармонические колебания – это колебания с постоянной амплитудой происходящие по закону синуса или косинуса.

Параметры гармонических колебаний. Постоянные величины А, Т, f, входящие в уравнение Acos( 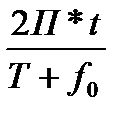)называются параметрами колебания. Рассмотрим их физический смысл.

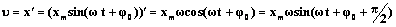
Из ур-я следует, что в случае, если соs(2p·t/Т + f) = ± 1, то значение модуля x максимально, т.е. |x| = xmax = A

Скорость – это производная от координаты по времени

Скорость при гармоническом колебательном движении также изменяется по гармоническому закону, но колебания скорости опережают колебания смещения по фазе на p/2.

Vmax=XmaxW:максимальная скорость колебательного движения(амплитуда колебаний скорости)

Ускорение – это производная от скорости по времени: a=V'=(x)'=x''(вторая производная)

Ускорение изменяется по гармоническому закону.

Amax=XmaxW^2:Макс ускорение

A=-amaxsin(wt+ф0):ускорение