Нормальная составляющая ускорения

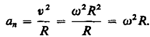
Основое уравнение динамики вращательного движения материальной точки - угловое ускорение точки при ее вращении вокруг неподвижной оси пропорционально вращающему моменту и обратно пропорционально моменту инерции.

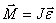
Taк как вектор скорости направлен по касательной к траектории, то вектор Dv_n, перпендикулярный вектору скорости, направлен к центру ее кривизны. Вторая составляющая ускорения, равная

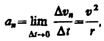
называется нормальной составляющей ускорения и направлена по нормали к траектории к центру ее кривизны (поэтому ее называют также центростремительным ускорением).

Полное ускорение тела есть геометрическая сумма тангенциальной и нормальной составляющих (рис.5):

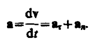
Итак, тангенциальная составляющая ускорения характеризует быстроту изменения скорости по модулю (направлена по касательной к траектории), а нормальная состав­ляющая ускорения — быстроту изменения скорости по направлению (направлена к цен­тру кривизны траектории).

В зависимости от тангенциальной и нормальной составляющих ускорения движе­ние можно классифицировать следующим образом:

1) 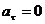, а_n= 0 — прямолинейное равномерное движение;

2) 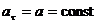, а_n= 0 — прямолинейное равнопеременное движение. При таком виде движения

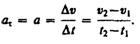
Если начальный момент времени t₁=0, а начальная скорость v₁=v₀, то, обозначив t₂=tи v₂=v, получим 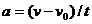, откуда

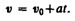
Проинтегрировав эту формулу в пределах от нуля до произвольного момента времени t, найдем, что длина пути, пройденного точкой, в случае равнопеременного движения

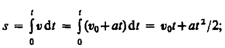
3) 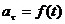, а_n= 0— прямолинейное движение с переменным ускорением;

4) 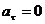, а_n= const. При 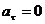скорость по модулю не изменяется, а изменяется по направлению. Из формулы a_n=v²/r следует, что радиус кривизны должен быть посто­янным. Следовательно, движение по окружности является равномерным;

5) 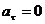, 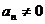— равномерное криволинейное движение;

6) 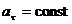, 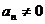— криволинейное равнопеременное движение;

7) 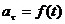, 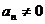— криволинейное движение с переменным ускорением.

Понятно, что линейные и соответствующие им угловые величины должны быть определенным образом связаны между собой. Найдем эти связи.

При повороте радиуса, проведенного в точку М (см. рис. 2), на угол φ точка пройдет по дуге окружности путь

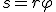. (1)

За малое время Δt точка проходит расстояние 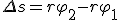, где φ2 и φ1 — углы поворота в конце и в начале интервала Δt. Разделив последнее равенство на Δt и учитывая, что 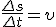и 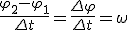, получим

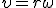. (2)

Заметим, что соотношение (2) связывает между собой линейную и угловую скорости не только при равномерном движении точки по окружности, но- и при неравномерном движении тоже. Изменение модуля скорости точки за время Δt есть 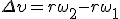, где ω2 и ω1 — угловые скорости в конце и в начале промежутка Δt. Разделим последнее равенство на Δt и учтем, что 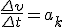и 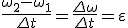, тогда касательное ускорение

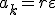. (3)

Соотношения (1), (2) и (3) дают для движущейся по окружности точки простую связь между линейными и угловыми величинами: линейная величина равна произведению радиуса окружности на соответствующую угловую величину. Эти соотношения получены нами для конкретной точки М колеса троллейбуса, но они справедливы и для любой другой точки вращающегося (как равномерно, так и неравномерно) тела.

4) Масса, импульс. Замкнутые системы. Закон сохранения импульса. Теорема о движении центра масс системы.

Первый закон Ньютона: всякая материальная точка (тело) сохраняет состояние покоя или равномерного прямолинейного движения до тех пор, пока воздействие со стороны других тел не заставит ее изменить это состояние. Стремление тела сохранять состояние покоя или равномерного прямолинейного движения называется инертностью. Поэтому первый закон Ньютона называют также законом инерции.

Инерциальной системой отсчета является такая система отсчета, относительно которой материальная точка, свободная от внешних воздействий, либо покоится, либо движется равномерно и прямолинейно. Первый закон Ньютона утверждает существование инерциальных систем отсчета.

Масса тела — физическая величина, являющаяся одной из основных характеристик материи, определяющая ее инерционные (инертная масса) и гравитационные (гравитационная масса) свойства. В настоящее время можно считать доказанным, что инертная и гравитационная массы равны друг другу (с точностью, не меньшей 10^–12 их значения).

сила— это векторная величина, являющаяся мерой механического воздействия на тело со стороны других тел или полей, в результате которого тело приобретает ускорение или изменяет свою форму и размеры.

Второй закон Ньютона — основной закон динамики поступательного движения — от­вечает на вопрос, как изменяется механическое движение материальной точки (тела) под действием приложенных к ней сил.

а ~F (т =const).

а = kF/m.

Соотношение (6.3) выражает второй закон Ньютона: ускорение, приобретаемое материальной точкой (телом), пропорционально вызывающей его силе, совпадает с нею по направлению и обратно пропорционально массе материальной точки (тела).

Учитывая, что масса материальной точки (тела) в классической механике есть величина постоянная, в выражении (6.4) ее можно внести под знак производной:

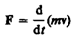
Векторная величина

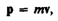
численно равная произведению массы материальной точки на ее скорость и имеющая направление скорости, называется импульсом (количеством движения) этой материаль­ной точки.

Подставляя (6.6) в (6.5), получим

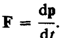
Это выражение — более общая формулировка второго закона Ньютона: скорость изме­нения импульса материальной точки равна действующей на нее силе. Выражение (6.7) называется уравнением движения материальной точки.

Единица силы в СИ — ньютон (Н): 1 Н — сила, которая массе 1 кг сообщает ускорение 1 м/с² в направлении действия силы:1 Н = 1 кг×м/с².

Второй закон Ньютона справедлив только в инерциальных системах отсчета.

Взаимодействие между материальными точками (телами) определяется третьим зако­ном Ньютона: всякое действие материальных точек (тел) друг на друга носит характер взаимодействия; силы, с которыми действуют друг на друга материальные точки, всегда равны по модулю, противоположно направлены и действуют вдоль прямой, соединяющей эти точки:

F₁₂ = – F₂₁

Замкнутая система тел в механике — совокупность физических тел, у которых взаимодействия с внешними телами отсутствуют.

Для вывода закона сохранения импульса рассмотрим некоторые понятия. Совокуп­ность материальных точек (тел), рассматриваемых как единое целое, называется механической системой. Силы взаимодействия между материальными точками механичес­кой системы называются — внутренними. Силы, с которыми на материальные точки системы действуют внешние тела, называются внешними. Механическая система тел, на которую не действуют внешние силы, называется замкнутой (или изолированной). Если мы имеем механическую систему, состоящую из многих тел, то, согласно третьему закону Ньютона, силы, действующие между этими телами, будут равны и проти­воположно направлены, т. е. геометрическая сумма внутренних сил равна нулю.

Рассмотрим механическую систему, состоящую из n тел, масса и скорость которых соответственно равныm₁, m₂,.... m_n, и v₁, v₂,..., v_n. Пусть 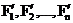— равнодейст­вующие внутренних сил, действующих на каждое из этих тел, a 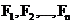— равно­действующие внешних сил. Запишем второй закон Ньютона для каждого из n тел механической системы:

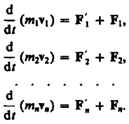
Складывая почленно эти уравнения, получаем

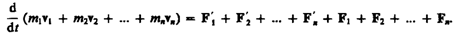
Но так как геометрическая сумма внутренних сил механической системы по третьему закону Ньютона равна нулю, то

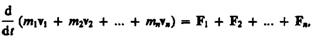
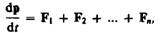(9.1)

где 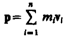— импульс системы. Таким образом, производная по времени от им­пульса механической системы равна геометрической сумме внешних сил, действующих на систему.

В случае отсутствия внешних сил (рассматриваем замкнутую систему)

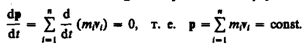
Последнее выражение и является законом сохранения импульса: импульс замкнутой системы сохраняется, т. е. не изменяется с течением времени.

Закон сохранения импульса справедлив не только в классической физике, хотя он и получен как следствие законов Ньютона. Эксперименты доказывают, что он выпол­няется и для замкнутых систем микрочастиц (они подчиняются законам квантовой механики). Этот закон носит универсальный характер, т. е. закон сохранения импуль­са — фундаментальный закон природы.

Закон сохранения импульса является следствием определенного свойства симмет­рии пространства — его однородности. Однородность пространства заключается в том, что при параллельном переносе в пространстве замкнутой системы тел как целого ее физические свойства и законы движения не изменяются, иными словами, не зависят от выбора положения начала координат инерциальной системы отсчета.

Центром масс (или центром инерции) системы материальных точек называется воображаемая точкаС,положение которой характеризует распределение массы этой системы. Ее ра­диус-вектор равен

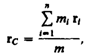
где m_i и r_i — соответственно масса и радиус-вектор i-й материальной точки; n — число материальных точек в системе; – масса системы. Скорость центра масс

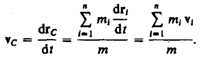
Учитывая, что pi = m_iv_i , a 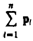есть импульс р системы, можно написать

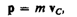(9.2)

т. е. импульс системы равен произведению массы системы на скорость ее центра масс.

Подставив выражение (9.2) в уравнение (9.1), получим

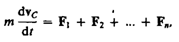(9.3)

т. е. центр масс системы движется как материальная точка, в которой сосредоточена масса всей системы и на которую действует сила, равная геометрической сумме всех внешних сил, приложенных к системе. Выражение (9.3) представляет собойзакон движения центра масс.

В соответствии с (9.2) из закона сохранения импульса вытекает, что центр масс замкнутой системы либо движется прямолинейно и равномерно, либо остается непо­движным.