Дифракция на пространственных решетках. Понятие пространственных решеток. Дифракция рентгеновских лучей. Условие Вульфа-Брэггов. Применение

История, физические принципы и применение голографии. Голограммы Френеля и Денисюка

Голография (от греч. «полная запись») — особый способ записи и последующего восстановления волнового поля, основанный на регистрации интерференционной кар­тины. Она обязана своим возникновением законам волновой оптики — законам ин­терференции и дифракции.

Этот принципиально новый способ фиксирования и воспроизведения пространст­венного изображения предметов изобретен английским физиком Д. Габором (1900—1979) в 1947 г. (Нобелевская премия 1971 г.). Экспериментальное воплощение и дальнейшая разработка этого способа (Ю. Н. Денисюком в 1962 г. и американскими физиками Э. Лейтом и Ю. Упатниексом в 1963 г.) стали возможными после появле­ния в 1960 г. источников света высокой степени когерентности — лазеров (см. § 233).

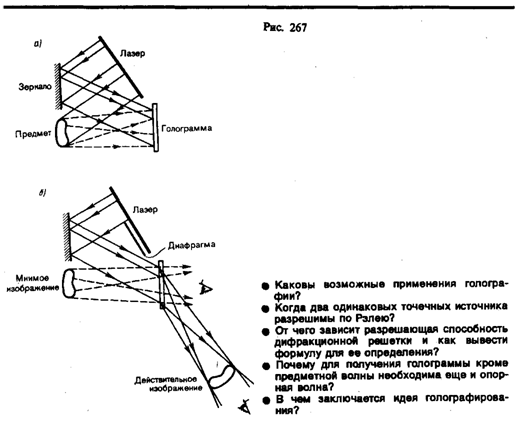
Практически эта идея может быть осуществлена с помощью принципиальной схемы, показанной на рис. 267, а. Лазерный пучок делится на две части, причем одна его часть отражается зеркалом на фотопластинку (опорная волна), а вторая попадает на фотопластинку, отразившись от предмета (предметная волна). Опорная и предмет­ная волны, являясь когерентными и накладываясь друг на друга, образуют на фотопла­стинке интерференционную картину. После проявления фотопластинки и получается голограмма — зарегистрированная на фотопластинке интерференционная картина, об­разованная при сложении опорной и предметной волн.

Нормальная и аномальная дисперсии. Групповая и фазовая в веществе

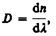
называемая дисперсией вещества, показывает, как быстро изменяется показатель прело­мления с длиной волны. Из рис. 269 следует, что показатель преломления для прозрач­ных веществ с уменьшением длины волны увеличивается; следовательно, величина dn/dl по модулю также увеличивается с уменьшением l. Такая дисперсия называется нормальной. Как будет показано ниже, ход кривой n(l) — кривой дисперсии — вблизи линий и полос поглощения будет иным: n уменьшается с уменьшением l. Такой ход зависимости n от l называется аномальной дисперсией.

На явлении нормальной дисперсии основано действие призменных спектрографов. Несмотря на их некоторые недостатки (например, необходимость градуировки, различ­ная дисперсия в разных участках спектра) при определении спектрального состава света, призменные спектрографы находят широкое применение в спектральном анали­зе. Это объясняется тем, что изготовление хороших призм значительно проще, чем изготовление хороших дифракционных решеток. В призменных спектрографах также легче получить большую светосилу.

Основные выводы

• световые волны поперечны, однако в естественном свете нет преимущественного направления колебаний;

• кристалл поляризатора пропускает лишь те волны, вектор которых имеет составляющую параллельную оси кристалла. (именно поэтому поляризатор ослабляет свет в два раза);

• для анализа света используется кристалл анализатора, который пропускает свет, когда его ось параллельна оси поляризатора.

Законы внешнего фотоэффекта

Закон Столетова: при неизменном спектральном составе электромагнитных излучений, падающих на фотокатод, фототок насыщения пропорционален энергетической освещенности катода (иначе: число фотоэлектронов, выбиваемых из катода за 1 с, прямо пропорционально интенсивности излучения):

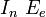и

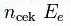
Максимальная начальная скорость фотоэлектронов не зависит от интенсивности падающего света, а определяется только его частотой.

Для каждого вещества существует красная граница фотоэффекта, то есть минимальная частота ν0 света (зависящая от химической природы вещества и состояния поверхности), ниже которой фотоэффект невозможен.

«Красная» грани́ца фотоэффе́кта — минимальная частота или максимальная длина волны света, при которой еще возможен внешний фотоэффект, то есть начальная кинетическая энергия фотоэлектронов больше нуля. Частота зависит только от работы выхода электрона:

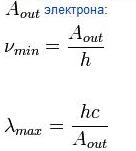
где A — работа выхода для конкретного фотокатода, h — постоянная Планка, а с — скорость света . Работа выхода зависит от материала фотокатода и состояния его поверхности. Испускание фотоэлектронов начинается сразу же, как только на фотокатод падает свет с частотой 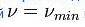или с длиной волны .

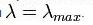Фотонная теория света.

Прежде всего, заметим, что в монохроматическом пучке все фотоны имеют одинаковую энергию (равную hν). Увеличение интенсивности светового пучка означает увеличение числа фотонов в пучке, но не сказывается на их энергии, если частота остается неизменной. Согласно теории Эйнштейна, электрон выбивается с поверхности металла при соударении с ним отдельного фотона. При этом вся энергия фотона передается электрону, а фотон перестает существовать. Т.к. электроны удерживаются в металле силами притяжения, для выбивания электрона с поверхности металла требуется минимальная энергия A (которая называется работой выхода и составляет, для большинства металлов, величину порядка нескольких электронвольт). Если частота ν падающего света мала, то энергии 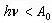и энергии фотона недостаточно для того, чтобы выбить электрон с поверхности металла. Если же 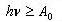, то электроны вылетают с поверхности металла, причем энергия в таком процессе сохраняется, т.е. энергия фотона (hν) равна кинетической энергии вылетевшего электрона плюс работе по выбиванию электрона из металла:

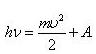
Уравне́ния Эйнште́йна (иногда встречается название «уравнения Эйнштейна-Гильберта»[1]) — уравнения гравитационного поля в общей теории относительности, связывающие между собой метрику искривлённого пространства-времени со свойствами заполняющей его материи. Термин используется и в единственном числе: «уравне́ние Эйнште́йна», так как в тензорной записи это одно уравнение, хотя в компонентах представляет собой систему уравнений.

Выглядят уравнения следующим образом:

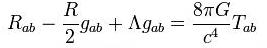
где 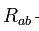— тензор Риччи, получающийся из тензора кривизны пространства-времени 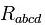посредством свёртки его по паре индексов, R — скалярная кривизна, то есть свёрнутый тензор Риччи, 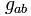— метрический тензор, 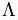— космологическая постоянная, а 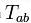представляет собой тензор энергии-импульса материи, ( — число пи, c — скорость света в вакууме, G — гравитационная постоянная Ньютона). Так как все входящие в уравнения тензоры симметричны, то в четырёхмерном пространстве-времени эти уравнения равносильны 4·(4+1)/2=10 скалярным уравнениям.

Одним из существенных свойств уравнений Эйнштейна является их нелинейность, приводящая к невозможности использования при их решении принципа суперпозиции.

Опыт Боте.

В этом опыте тонкая металлическая фольга облучалась рентгеновским излучением низкой интенсивности. При этом фольга сама становилась источником слабого вторичного излучения. Исходя из классических волновых представлений, это излучение должно распределяться в пространстве равномерно во всех направлениях. В этом случае два счётчика, находившиеся слева и справа от фольги, должны были фиксировать его одновременно. Однако результат опыта оказался прямо противоположным: излучение фиксировалось либо правым, либо левым счётчиком и никогда обоими одновременно. Следовательно, поглощение идёт отдельными квантами. Опыт, таким образом, подтвердил исходное положение фотонной теории излучения, и стал, тем самым, ещё одним экспериментальным доказательством квантовых свойств электромагнитного излучения.

Фотон — безмассовая нейтральная частица.

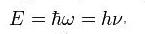Энергия фотона.

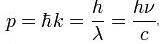Импульс фотона.

38. Эффект Комптона (Комптон-эффект) — явление изменения длины волны электромагнитного излучения вследствие упругого рассеивания его электронами.

При рассеянии фотона на покоящемся электроне частоты фотона V и V’ (до и после рассеяния соответственно) связаны соотношением:

.

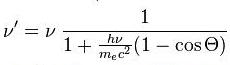где 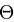— угол рассеяния (угол между направлениями распространения фотона до и после рассеяния).

Перейдя к длинам волн:

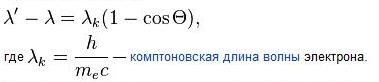
Для электрона 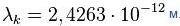Уменьшение энергии фотона после комптоновского рассеяния называется комптоновским сдвигом. В классической электродинамике рассеяние электромагнитной волны на заряде (томсоновское рассеяние) не сопровождается уменьшением её частоты.

Объяснить эффект Комптона в рамках классической электродинамики невозможно. С точки зрения классической физики электромагнитная волна является непрерывным объектом и в результате рассеяния на свободных электронах изменять свою длину волны не должна. Эффект Комптона является прямым доказательством квантования электромагнитной волны, другими словами подтверждает существование фотонов. Эффект Комптона является ещё одним доказательством справедливости корпускулярно-волнового дуализма микрочастиц.

39. Тормозное излучение — электромагнитное излучение, испускаемое заряженной частицей при её рассеянии (торможении) в электрическом поле. Иногда в понятие «тормозное излучение» включают также излучение релятивистских заряженных частиц, движущихся в макроскопических магнитных полях (в ускорителях, в космическом пространстве), и называют его магнитотормозным; однако более употребительным в этом случае является термин «синхротронное излучение».

Согласно классической электродинамике, которая достаточно хорошо описывает основные закономерности тормозного излучения, его интенсивность пропорциональна квадрату ускорения заряженной частицы. Так как ускорение обратно пропорционально массе m частицы, то в одном и том же поле тормозное излучение легчайшей заряженной частицы — электрона будет, например, в миллионы раз мощнее излучения протона. Поэтому чаще всего наблюдается и практически используется тормозное излучение, возникающее при рассеянии электронов на электростатическом поле атомных ядер и электронов; такова, в частности, природа рентгеновских лучей в рентгеновских трубках и гамма-излучения, испускаемого быстрыми электронами при прохождении через вещество.

Причиной значительного тормозного излучения может быть тепловое движение в горячей разреженной плазме. Элементарные акты тормозного излучения, называются в этом случае тепловым, обусловлены столкновениями заряженных частиц, из которых состоит плазма. Космическое рентгеновское излучение, наблюдение которого стало возможным с появлением искусственных спутников Земли, частично является, по-видимому, тепловым тормозным излучением. Тормозное рентгеновское и гамма-излучение широко применяются в технике, медицине, в исследованиях по биологии, химии и физике.

40. Характеристическое излучение.

Рентгеновские лучи возникают при сильном ускорении заряженных частиц (тормозное излучение), либо при высокоэнергетических переходах в электронных оболочках атомов или молекул. Оба эффекта используются в рентгеновских трубках. Основными конструктивными элементами таких трубок являются металлические катод и анод (ранее называвшийся также антикатодом). В рентгеновских трубках электроны, испущенные катодом, ускоряются под действием разности электрических потенциалов между анодом и катодом (при этом рентгеновские лучи не испускаются, так как ускорение слишком мало) и ударяются об анод, где происходит их резкое торможение. При этом за счёт тормозного излучения происходит генерация излучения рентгеновского диапазона, и одновременно выбиваются электроны из внутренних электронных оболочек атомов анода. Пустые места в оболочках занимаются другими электронами атома. При этом испускается рентгеновское излучение с характерным для материала анода спектром энергий (характеристическое излучение, частоты определяются законом Мозли: где Z — атомный номер элемента анода, A и B — константы для определённого значения главного квантового числа n электронной оболочки)

Закон Мозли — закон, связывающий частоту спектральных линий характеристического рентгеновского излучения атома химического элемента с его порядковым номером. Экспериментально установлен английским физиком Генри Мозли в 1913 году.

Формулировка закона Мозли

Согласно Закону Мозли, корень квадратный из частоты спектральной линии характеристического излучения элемента есть линейная функция его порядкового номера :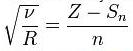

где R— постоянная Ридберга, S — постоянная экранирования, n — главное квантовое число. На диаграмме Мозли зависимость от Y представляет собой ряд прямых (К-, L-, М- и т. д. серии, соответствующие значениям n = 1, 2, 3,...).

Закон Мозли явился неопровержимым доказательством правильности размещения элементов в периодической системе элементов Д. И. Менделеева и содействовал выяснению физического смысла Z.

В соответствии с Законом Мозли, рентгеновские характеристические спектры не обнаруживают периодических закономерностей, присущих оптическим спектрам. Это указывает на то, что проявляющиеся в характеристических рентгеновских спектрах внутренние электронные оболочки атомов всех элементов имеют аналогичное строение.

Более поздние эксперименты выявили некоторые отклонения от линейной зависимости для переходных групп элементов, связанные с изменением порядка заполнения внешних электронных оболочек, а также для тяжёлых атомов, появляющиеся в результате релятивистских эффектов (условно объясняемых тем, что скорости внутренних электронов сравнимы со скоростью света).

В зависимости от ряда факторов — от числа нуклонов в ядре атома (изотопический сдвиг), состояния внешних электронных оболочек (химический сдвиг) и пр. — положение спектральных линий на диаграмме Мозли может несколько изменяться. Изучение этих сдвигов позволяет получать детальные сведения об атоме.

41.

Давление электромагнитного излучения, давление света — давление, которое оказывает световое (и вообще электромагнитное) излучение, падающее на поверхность тела.

Экспериментально световое давление впервые исследовал П. Н. Лебедев в 1899 г. В его опытах в вакуумированном сосуде на тонкой серебряной нити подвешивались крутильные весы, к коромыслам которых были прикреплены тонкие диски из слюды и различных металлов. Главной сложностью было выделить световое давление на фоне радиометрических и конвективных сил (сил, обусловленных разностью температуры окружающего газа с освещённой и неосвещённой стороны). Кроме того поскольку в то время не были разработаны вакуумные насосы, отличные от простых механических, Лебедев не имел возможности проводить свои опыты в условиях даже среднего, по современной классификации, вакуума.

Путем попеременного облучения разных сторон крылышек Лебедев нивелировал радиометрические силы и получил удовлетворительное (±20 %) совпадение с теорией Максвелла. Позднее, в 1907—1910 гг. Лебедев провёл более точные опыты по изучению давления света в газах и также получил приемлемое согласие с теорией[1].

42.

Корпускуля́рно-волново́й дуали́зм — принцип, согласно которому любой объект может проявлять как волновые, так и корпускулярные свойства. Был введён при разработке квантовой механики для интерпретации явлений, наблюдаемых в микромире, с точки зрения классических концепций. Дальнейшим развитием принципа корпускулярно-волнового дуализма стала концепция квантованных полей в квантовой теории поля.

Как классический пример, свет можно трактовать как поток корпускул (фотонов), которые во многих физических эффектах проявляют свойства электромагнитных волн. Свет демонстрирует свойства волны в явлениях дифракции и интерференции при масштабах, сравнимых с длиной световой волны. Например, даже одиночные фотоны, проходящие через двойную щель, создают на экране интерференционную картину, определяемую уравнениями Максвелла[1].

Тем не менее, эксперимент показывает, что фотон не есть короткий импульс электромагнитного излучения, например, он не может быть разделён на несколько пучков оптическими делителями лучей, что наглядно показал эксперимент, проведённый французскими физиками Гранжье, Роже и Аспэ в 1986 году[2]. Корпускулярные свойства света проявляются при фотоэффекте и в эффекте Комптона. Фотон ведет себя и как частица, которая излучается или поглощается целиком объектами, размеры которых много меньше его длины волны (например, атомными ядрами), или вообще могут считаться точечными (например, электрон).

В настоящий момент концепция корпускулярно-волнового дуализма представляет лишь исторический интерес, так как служила только интерпретацией, способом описать поведение квантовых объектов, подбирая ему аналогии из классической физики. На деле квантовые объекты не являются ни классическими волнами, ни классическими частицами, приобретая свойства первых или вторых лишь в некотором приближении. Методологически более корректной является формулировка квантовой теории через интегралы по траекториям (пропагаторная), свободная от использования классических понятий.

43.

Опыт Дэвиссона-Джермера — физический эксперимент по дифракции электронов, проведённый в 1927 г. американскими учёными Клинтоном Дэвиссоном и Лестером Джермером.

Проводилось исследование отражения электронов от монокристалла никеля. Установка включала в себя монокристалл никеля, сошлифованный под углом и установленный на держателе. На плоскость шлифа направлялся перпендикулярно пучок монохроматических электронов. Скорость электронов определялась напряжением U на электронной пушке:

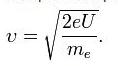
Под углом 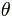к падающему пучку электронов устанавливался цилиндр Фарадея, соединённый с чувствительным гальванометром. По показаниям гальванометра определялась интенсивность отражённого от кристалла электронного пучка. Вся установка находилась в вакууме.

В опытах измерялась интенсивность рассеянного кристаллом электронного пучка в зависимости от угла рассеяния 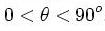от азимутального угла 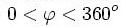, от скорости V электронов в пучке.

Опыты показали, что имеется ярко выраженная селективность (выборочность) рассеяния электронов. При различных значениях углов и скоростей, в отражённых лучах наблюдаются максимумы и минимумы интенсивности. Условие максимума:

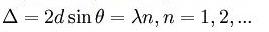
Здесь d— межплоскостное расстояние.

Таким образом наблюдалась дифракция электронов на кристаллической решётке монокристала. Опыт явился блестящим подтверждением существования у микрочастиц волновых свойств.

44.

Для частиц не очень высокой энергии, движущихся со скоростью 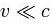(скорости света), импульс равен p=mv (где m — масса частицы), и 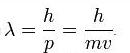. Следовательно, длина волны де Бройля тем меньше, чем больше масса частицы и её скорость. Например, частице с массой в 1 г, движущейся со скоростью 1 м/с, соответствует волна де Бройля 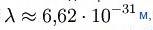, что лежит за пределами доступной наблюдению области. Поэтому волновые свойства несущественны в механике макроскопических тел. Для электронов же с энергиями от 1 эВ до 10 000 эВ длина волны де Бройля лежит в пределах от ~ 1 нм до 10−2 нм, то есть в интервале длин волн рентгеновского излучения. Поэтому волновые свойства электронов должны проявляться, например, при их рассеянии на тех же кристаллах, на которых наблюдается дифракция рентгеновских лучей.

Первое подтверждение гипотезы де Бройля было получено в 1927 году в опытах американских физиков К. Дэвиссона и Л. Джермера. Пучок электронов ускорялся в электрическом поле с разностью потенциалов 100—150 В (энергия таких электронов 100—150 эВ, что соответствует 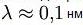) и падал на кристалл никеля, играющий роль пространственной дифракционной решётки. Было установлено, что электроны дифрагируют на кристалле, причём именно так, как должно быть для волн, длина которых определяется соотношением де Бройля.[1]

Подтвержденная на опыте идея де Бройля о двойственной природе микрочастиц — корпускулярно-волновом дуализме — принципиально изменила представления об облике микромира. Поскольку всем микрообъектам (за ними сохраняется термин «частица») присущи и корпускулярные, и волновые свойства, то, очевидно, любую из этих «частиц» нельзя считать ни частицей, ни волной в классическом понимании. Возникла потребность в такой теории, в которой волновые и корпускулярные свойства материи выступали бы не как исключающие, а как взаимно дополняющие друг друга. В основу такой теории — волновой, или квантовой механики — и легла концепция де Бройля. Это отражается даже в названии «волновая функция» для величины, описывающей в этой теории состояние системы. Квадрат модуля волновой функции определяет вероятность состояния системы, и поэтому о волнах де Бройля часто говорят[3] как о волнах вероятности (точнее, амплитуд вероятности). Для свободной частицы с точно заданным импульсом p (и энергией 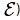, движущейся вдоль оси x, волновая функция имеет вид[1]:

45.

Принцип неопределённости Гейзенбе́рга в квантовой механике — фундаментальное неравенство (соотношение неопределённостей), устанавливающее предел точности одновременного определения пары характеризующих квантовую систему физических наблюдаемых (см. физическая величина), описываемых некоммутирующими операторами (например, координаты и импульса, тока и напряжения, электрического и магнитного поля). Соотношение неопределенностей[* 1] задаёт нижний предел для произведения среднеквадратичных отклонений пары квантовых наблюдаемых. Принцип неопределённости, открытый Вернером Гейзенбергом в 1927 г., является одним из краеугольных камней квантовой механики.

Если имеется несколько (много) идентичных копий системы в данном состоянии, то измеренные значения координаты и импульса будут подчиняться определённому распределению вероятности — это фундаментальный постулат квантовой механики. Измеряя величину среднеквадратического отклонения 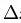x координаты и среднеквадратического отклонения 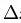p импульса, мы найдем что:

,

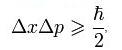где ħ — приведённая постоянная Планка.

В некоторых случаях «неопределённость» переменной определяется как наименьшая ширина диапазона, который содержит 50 % значений, что, в случае нормального распределения переменных, приводит для произведения неопределённостей к большей нижней границе ħ.

Отметим, что это неравенство даёт несколько возможностей — состояние может быть таким, что x может быть измерен с высокой точностью, но тогда p будет известен только приблизительно, или наоборот p может быть определён точно, в то время как x — нет. Во всех же других состояниях и p, и x могут быть измерены с «разумной» (но не произвольно высокой) точностью.

46.

Волнова́я фу́нкция, 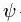или пси-функция — комплекснозначная функция, используемая в квантовой механике для описания чистого состояния системы. Является коэффициентом разложения вектора состояния по базису (обычно координатному):

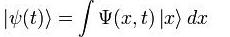
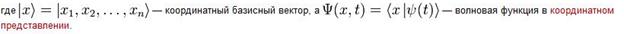
Физический смысл волновой функции заключается в том, что согласно копенгагенской интерпретации квантовой механики плотность вероятности нахождения частицы в данной точке конфигурационного пространства в данный момент времени считается равной квадрату абсолютного значения волновой функции этого состояния в координатном представлении.

Вероятностный смысл волновой функции накладывает определенные ограничения, или условия, на волновые функции в задачах квантовой механики. Эти стандартные условия часто называют условиями регулярности волновой функции.

1. Условие конечности волновой функции. Волновая функция не может принимать бесконечных значений, таких, что интеграл 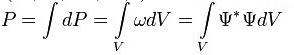станет расходящимся. Следовательно, это условие требует, чтобы волновая функция была квадратично интегрируемой функцией. В частности, в задачах с нормированной волновой функцией квадрат модуля волновой функции должен стремиться к нулю на бесконечности.

2. Условие однозначности волновой функции. Волновая функция должна быть однозначной функцией координат и времени, так как плотность вероятности обнаружения частицы должна определяться в каждой задаче однозначно. В задачах с использованием цилиндрической или сферической системы координат условие однозначности приводит к периодичности волновых функций по угловым переменным.

3. Условие непрерывности волновой функции. В любой момент времени волновая функция должна быть непрерывной функцией пространственных координат. Кроме того, непрерывными должны быть также частные производные волновой функции , 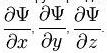, . Эти частные производные функций лишь в редких случаях задач с идеализированными силовыми полями могут терпеть разрыв в тех точках пространства, где потенциальная энергия, описывающая силовое поле, в котором движется частица, испытывает разрыв второго рода.

47.

Стационарное уравнение Шрёдингера

Форма уравнения Шрёдингера показывает, что относительно времени его решение должно быть простым, поскольку время входит в это уравнение лишь через первую производную в правой части. Действительно, частное решение для специального случая, когда Ep не является функцией времени, можно записать в виде:

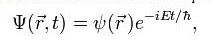
где функция 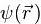должна удовлетворять уравнению:

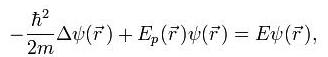
которое получается из уравнения Шрёдингера (1) при подстановке в него указанной выше формулы для 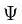(2). Заметим, что это уравнение вообще не содержит времени; в связи с этим оно называется стационарным уравнением Шрёдингера (уравнение Шрёдингера, не содержащее времени).

Выражение (2) является лишь частным решением зависящего от времени уравнения Шрёдингера (1), общее решение представляет собой линейную комбинацию всех частных решений вида (2). Зависимость функции 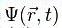от времени проста, но зависимость её от координаты не всегда имеет элементарный вид, так как уравнение (3) при одном выборе вида потенциальной функции 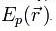совершенно отличается от того же уравнения при другом выборе этой функции. В действительности, уравнение (3) может быть решено аналитически лишь для небольшого числа частных типов функции .

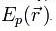Важное значение имеет интерпретация величины E в уравнении (2). Она производится следующим путём: временна́я зависимость функции 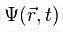в уравнении (2) имеет экспоненциальный характер, причём коэффициент при t в показателе экспоненты выбран так, что правая часть уравнения (3) содержит просто постоянный множитель E. В левой же части уравнения (3) функция 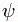умножается на потенциальную энергию 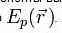. Следовательно, из соображений размерности вытекает, что величина E должна иметь размерность энергии. Единственной величиной с размерностью энергии, которая постоянна в механике, является полная (сохраняющаяся) энергия системы; таким образом, можно предполагать, что E представляет собой полную энергию. Согласно физической интерпретации уравнения Шрёдингера , E действительно является полной энергией частицы при движении, описываемом функцией .

Деление ядер

при поглощении нейтронов ураном происходит деление ядра на два осколка.

92U + n → 56Ba +36Kr + kn

где k > 1.

При делении ядра урана тепловой нейтрон с энергией ~ 0,1 эВ освобождает энергию ~ 200 МэВ.

Этот процесс сопровождается появлением нейтронов, способных вызывать деление других ядер урана, – цепная реакция деления. Таким образом, один нейтрон может дать начало разветвленной цепи делений ядер, причем число ядер, участвующих в реакции деления будет экспоненциально возрастать

Масса,

Среднее время жизни,

Спин,

Электрический заряд,

магнитный момент.

Странные частицы

В начале 50-х годов ХХ в. было обнаружено, что некоторые из недолго до того открытых частиц, а именно К, Ʌ, Sведут себя странно в двух отношениях. Во-первых, они всегда рождаются парами. Например, реакция проходит с вероятностью, близкой к 1, а реакция π– + p → K0 + n никогда не наблюдалась. Это казалось тем боле странным, что вторая реакция не нарушала ни одного из известных законов сохранения и для её осуществления было достаточно энергии.Во-вторых, хотя рождение странныхчастиц (как их стали называть) было обусловлено сильным взаимодействием (т.е. происходило с большой вероятностью), их распады не имели характерного для сильного взаимодействия времени жизни, хотя они и распадались на сильно взаимодействующие частицы например,

K → 2π, ∑+ → p+ π0.

Время жизни странных частиц оказалось в пределах от 10–10 до 10–8с, что характерно для слабого взаимодействия.

Для объединения этих фактов были введены новое квантовое число странностьи новый закон сохранения (сохранности). Так вот в первой реакции странность частиц до реакции совпадает со странностью частиц после реакции, а во второй реакции странность не сохраняется и поэтому эта реакция не идет. Для объяснения особенностей распада странных частиц предполагается, что странность сохраняется в сильном взаимодействии и не сохраняется в слабом взаимодействии. Следовательно, хотя закон сохранения запрещает распад странных частиц на более лёгкие не странные частицы, за счёт сильного взаимодействия, такие распады и происходят за счёт слабого взаимодействия. Но слабые распады происходят гораздо медленнее, что соответствует большим временам жизни. Сохранение странности оказалось первым примером «частично сохраняющейся величины»: странность сохраняется в сильном и не сохраняется в слабом взаимодействии.

Кварки и очарование

Почти все наблюдаемые частицы принадлежат одному из двух семейств: лептонам и адронам. Основное различие между ними состоит в том, что адроны не участвуют в сильном взаимодействии, а лептоны участвуют. Другое важное различие состоит в том, что в 60-х годах были известны четыре лептона (e–, µ–, νe,νµ) и их античастицы и более сотни адронов. Лептоны считаются элементарными частицами, т.к. они, насколько известно, не распадаются на составные части, не обнаруживают никакой внутренней структуры и не имеют определённого размера. Попытки определить размеры лептонов показали, что верхний предел составляет 10–18 м.

С другой стороны, адроны оказались более сложными частицами. Эксперименты показали, что адроны обладают внутренней структурой, и их обилие наводит на мысль, что адроны совсем не элементарны. Для решения этой проблемы М. Гелл-Манн и Г. Цвейг в 1963 г. независимо высказали идею, согласно которой все известные адроны неэлементарны, а построены из трёх более фундаментальных точечных объектов, называемых кварками.

Подобно лептонам кварки представляют собой истинно элементарные частицы.

Три «сорта» кварков были обозначены буквами

u(up – вверх),

d(down – вниз),

s(strange – странный).

Привычное свойство-спин: векторное сложение-спин равен сумме спинов кварков.

Непривычное свойство-дробные заряды: Заряд составной частицы равен сумме зарядов кварков

Четвертый кварк получил название очарованный. Его электрический заряд должен быть равен 2/3е.

Кроме того, четвёртый кварк должен обладать ещё одним свойством, отличающим его от трёх остальных кварков. Это новое свойство или квантовое число, было названо очарованием. Предполагалось, что очарование с ведёт себя подобно странности: сохраняется в сильном и электромагнитном взаимодействии и не сохраняется в слабом взаимодействии.

У нового очарованного кварка с = +1, у его антикварка с = – 1.

Исходя из симметрии природы физики предположили существование ещё двух кварков:

b-кварки (bottom – низ или beauty - красивый)

t-кварки (top – высший или truth - истинный). Соответственно новые свойства (квантовые числа), отличающие новые кварки от ранее известных, называются t- и b-свойствами или истиной и красотой.

Фотоэффект и его виды

Различают фотоэффект внешний, внутренний и вентильный. Внешним фотоэффектом называется испускание электронов веществом под действием электромагнитного излучения.

Внутренний фотоэффект – это вызванные электромагнитным излучением переходы электронов внутри полупроводника или диэлектрика из связанных состояний в свободные без вылета наружу.

Вентильный фотоэффект (разновидность внутреннего фотоэффекта) – возникновение эдс (фото-эдс) при освещении контакта двух разных полупроводников или полупроводника и металла (при отсутствии внешнего электрического поля).

Опыт Столетова.

Первые фундаментальные исследования фотоэффекта выполнены русским ученым А.Г. Столетовым. Два электрода (катод К из исследуемого материала и анод А (металлическая сетка)) в вакуумной трубке подключены к батарее так, что с помощью потенциометра R можно изменять не только значение, но и знак подаваемого на них напряжения. Ток, возникающий при освещении катода монохроматическим светом (через кварцевое стекло), измеряется включенным в цепь миллиамперметром. В 1899 Дж. Дж. Томпсон и Ф. Ленард доказали, что при фотоэффекте свет выбивает из вещества электроны.Вольтамперная характеристика (ВАХ) фотоэ

Наши рекомендации