Момент инерции твёрдого тела. Теорема Штейнера.

Ответы к экзамену по физике.

1. Кинематика поступательного движения материальной точки. (путь, перемещение, скорость, ускорение).

Кинематика – изучает движение тел, не рассматривая причины, которые это движение обуславливает.

Мат.точка – не имеет размеров, но в мат.точке сосредоточенна масса всего тела.

Поступательное – движение при котором прямая связанная с телом остаётся || самой себе.

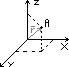
A = f(x,y,z)

r = f(t)

Кинетические ур-я движения мат.точки:

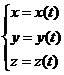
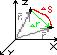
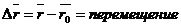
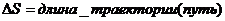
Траектория – линия описываемая мат.точкой в пространстве.

Перемещение – приращение радиуса-вектора точки за рассматриваемый промежуток времени.

Скорость – Быстрота движения мат.точки.

Вектором средней скорости< 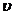> называется отношение приращения 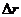радиуса-вектора точки к промежутку времени .

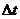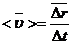
Мгновенная скорость – величина, равная первой производной радиуса-вектора движущейся точки по времени.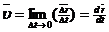

Модуль мгновенной скорости равен первой производной пути по времени.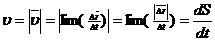

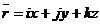
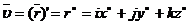
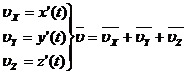Компоненты 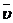равны производным от координат по времени.

Равномерное – движение при котором за равные промежутки времени тело проходит одинаковые пути.

Неравномерное – движение при котором скорость меняется как по модулю так и по направлению.

; ; ; ;

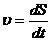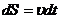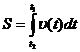2. Ускорение и его составляющие.

Ускорение – физ.величина, определяющая быстроту изменения скорости, как по модулю, так и по направлению.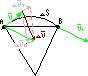

Средним ускорением неравномерного движения в интервале времени от t до t+ 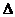t называется векторная величина равная отношению изменения скорости 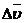к интервалу времени 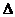t: .

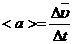Мгновенным ускорением 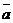мат.точки в момент времени t будет предел среднего ускорения. . .

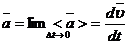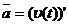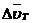определяет 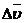по модулю.

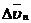определяет 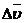по направлению.

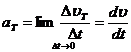, т.е. равна первой производной по времени от модуля скорости, определяя тем самым быстроту изменения скорости по модулю.

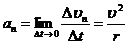, нормальная составляющая ускорения направлена по нормали к траектории к центру её кривизны (поэтому её также называют центростремительным ускорением).

Полное ускорение тела есть геометрическая сумма тангенциальной и нормальной составляющих.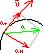

Если а_н=?,а_т=?

3. 1,2,3 законы Ньютона.

В основе Динамики мат.точки лежат три закона Ньютона.

Первый закон Ньютона –всякая материальная точка (тело) сохраняет состояние покоя или равномерного прямолинейного движения до тех пор, пока воздействие со стороны других тел не заставит её изменить это состояние.

Инертность – стремление тела сохранять состояние покоя или равномерного прямолинейного движения.

Законы Ньютона выполняются только в инерциальной системе отсчёта.

Инерциальная система отсчёта – система, которая либо покоится, либо движется равномерно и прямолинейно относительно какой то другой инерциальной системы.

Масса тела – физ.величина, являющаяся одной из основных характеристик материи, определяющая её инерционные (инертная масса) и гравитационные (гравитационная масса) св-ва.

Сила – векторная величина, являющаяся мерой механического воздействия на тело со стороны других тел или полей, в результате которого тело приобретает ускорение или изменяет свою форму и размеры.

Обозначения(…)

Второй закон Ньютона – ускорение, приобретаемое материальной точкой (телом), пропорционально вызывающей его силе, совпадает с нею по направлению и обратно пропорционально массе материальной точки.

; ; ;

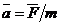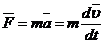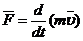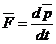
Импульс (кол-во движения) – векторная величина, численно равная произведению массы материальной точки на её скорость и имеющая направление скорости.

Более общая формулировка 2-го закона Н.(уравнение движения мт): скорость изменения импульса материальной точки равна действующей на неё силе.

Следствие из 2зН: принцип независимости действия сил: если на мт действует одновременно несколько сил, то каждая из этих сил сообщает мт ускорение согласно 2зН, как будто других сил не было.

Третий закон Ньютона. Всякое действие мт (тел) друг на друга, носит характер взаимодействия; силы, с которыми действуют друг на друга мт, всегда равны по модулю, противоположно направлены и действуют вдоль прямой, соединяющей эти точки.

4. Импульс тела, сила. Закон сохранения импульса.

Импульс (кол-во движения) – векторная величина, численно равная произведению массы материальной точки на её скорость и имеющая направление скорости.

Сила – векторная величина, являющаяся мерой механического воздействия на тело со стороны других тел или полей, в результате которого тело приобретает ускорение или изменяет свою форму и размеры.

Внутренние силы – силы взаимодействия между мт механической системы.

Внешние силы – силы, с которыми на мт системы действуют внешние тела.

Замкнутая – механическая система тел, на которую не действуют внешние силы.

В механической системе тел, по 3-му закону Ньютона, силы, действующие между этими телами, будут равны и противоположно направлены, т.е. геометрическая сумма внутренних сил равна 0.

Запишем 2зН, для каждого из n тел механической системы(мс):

…………………

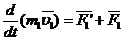
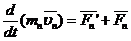
Сложим эти ур-я:

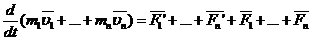
Т.к. геометрическая сумма внутренних сил мс по 3зН равна 0, то:

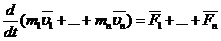
или:

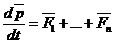
где 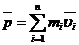- импульс системы.

В случае отсутствия внешних сил(замкнутая система):

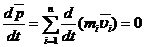, т.е.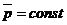

Это и есть закон сохранения импульса:импульс замкнутой системы сохраняется, т.е. не изменяется с течением времени.

5. Центр масс движение центра масс.

Центр масс (центр инерции) системы мт называется воображаемая точка С, положение которой характеризует распределение массы этой системы.

Радиус-вектор этой точки равен:

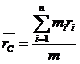
Скорость центра масс (цм):

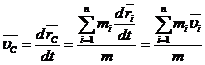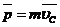; , т.е. импульс системы равен произведению массы системы на скорость её центра масс.

Т.к. 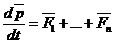то: 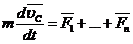, т.е.:

Закон движения центра масс: центр масс системы движется как мт, в которой сосредоточена масса всей системы и на которую действует сила, равная геометрической сумме всех внешних сил, действующих на систему.

6. Уравнение движения тела переменной массы.

Уравнение движения тела переменной массы (на примере ракеты):

Если в момент времени t масса ракеты m, а её скорость 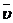, то по истечении времени dt её масса уменьшится на dm и станет равной m-dm, а скорость станет равной 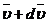. Изменение импульса системы за отрезок времени dt: 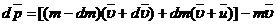, где u – скорость истечения газов, относительно ракеты. Отсюда: 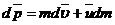(учли, что 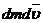- малый по сравнению с остальными).

Если на систему действуют внешние силы, то 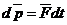: 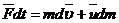, или: 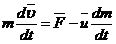, член 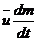- реактивная сила ( 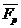), если 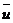противоположен 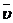, то ракета ускоряется, а если совпадает, тот тормозится, т.о.: уравнение движения тела переменной массы: .

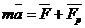Если на ракету не действуют внешние силы ( 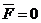), и u=const, то: 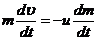, отсюда: 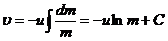, Если в начальный момент времени скорость равна 0, а масса равна m₀, то 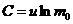, следовательно: 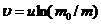. Это соотношение – Формула Циолковского, она показывает, что:

1) чем конечная масса (m), тем должна быть m₀.

2) чем u, тем может быть m при данной стартовой скорости.

7. Кинематика вращательного движения материальной точки.

Угловая скорость – векторная величина, равная первой производной угла поворота тела по времени.

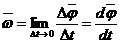
Вектор 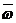направлен вдоль оси вращения по правилу правого винта.

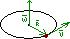
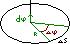
Линейная скорость точки:

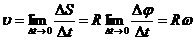
В векторном виде: 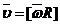, при этом модуль равен: .

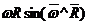Если 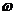=const, то вращение равномерное.

Период вращения (Т) – время, за которое точка совершает один полный оборот. ( ) .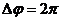

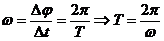Частота вращения (n) – число полных оборотов, совершаемых телом при равномерном его движении по окружности, в единицу времени. ; .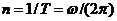

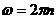Угловое ускорение – векторная величина, равная первой производной угловой скорости по времени: 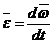. При ускоренном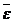 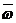, при замедленном .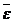

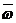Тангенциальная составляющая ускорения: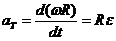

Нормальная составляющая: .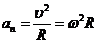

Формулы связи линейных и угловых величин:

, , , .

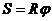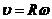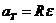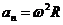При :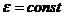

, .

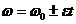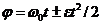8. Момент силы.

Момент силы F относительно неподвижной точки О называется физическая величина, определяемая векторным произведением радиуса-вектора r, проведённого из точки О в точку А приложения силы, на силу F.

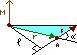
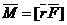, здесь 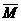- псевдовектор, его направление совпадает с направлением поступательного движения правого винта при его вращении от 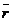к .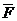

Модуль момента силы равен .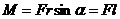

Момент силы относительно неподвижной оси z – скалярная величина 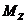, равная проекции на эту ось вектора 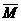момента силы, определённого относительно произвольной точки О данной оси z. Значение момента не зависит от выбора положения точки О на данной оси.

Основное уравнение МКТ.

Для вывода основного уравнения МКТ рассмотрим одноатомный идеальный газ. Предположим, что молекулы газа движутся хаотически, число взаимных столкновений между молекулами газа пренебрежимо мало, по сравнению с числом удара о стенки сосуда.

Выделим на стенке сосуда элементарную площадку 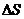, и вычислим давление, оказываемое на эту площадку. При каждом соударении молекула, движущаяся перпендикулярно площадке передаёт ей импульс: 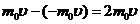. За время 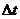площадки достигнут, только те молекулы, которые находятся в объёме цилиндра с основанием 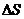и высотой 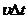. Число этих молекул равно 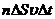(n-концентрация).

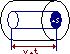
Необходимо учесть, что реально молекулы движутся к площадке под разными углами, и имеют различные скорости, причём скорость молекул при каждом соударении меняется. Для упрощения расчётов хаотическое движение молекул заменяют движением вдоль 3-х взаимно перпендикулярных направлений, так что в любой момент движения вдоль каждого из них движется 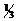молекул, причём половина молекул ( 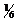) движется вдоль данного направления в одну сторону, половина в другую. Тогда число ударов молекул, движущихся в заданном направлении, о площадку 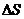будет 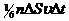. При столкновении с площадкой эти молекулы предадут ей импульс

,

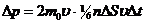
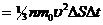тогда давление газа на стенку равно:

Средняя квадратичная скорость:

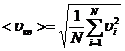
хар-ет всю совокупность молекул газа.

С учётом этой формулы:

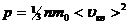
Это и есть основное уравнение МКТ.

Учтя, что 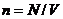получим:

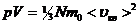,или

,

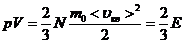где Е – суммарная кинетическая энергия поступательного движения всех молекул.

Т.к. 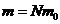, то:

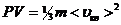
Для одного моля газа m=M ( M – молярная масса):

,

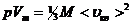где V_m- молярный объём. По уравнению Менделеева – Клапейрона pV_m=RT, т.о.:

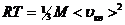, откуда:

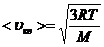
т.к. 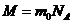, то

,

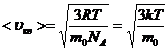где 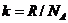- постоянная Больцмана.

Средняя кинетическая энергия поступательного движения одной молекулы иг:

.

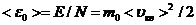
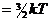Теплоёмкость.

Если в одной области газа средняя кинетическая энергия молекул больше, чем в другой, то с течением времени вследствие постоянных столкновений молекул происходит процесс выравнивания средних кинетических энергий молекул, т.е. выравнивание температур.

Перенос энергии в форме теплоты подчиняется закону Фурье:

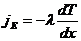, где 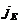-плотность тепловогопотока – величина, определяемая энергией, переносимой в форме теплоты в единицу времени через единичную площадку, перпендикулярно оси х. Знакминус показывает, что переносится в направлении убывания температуры. Теплопроводность 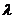численно равна плотности теплового потока при градиенте температуры, равном единице.

Можно показать, что

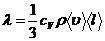, где 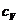-удельная теплоёмкость газа при постоянном объёме(количество теплоты, необходимоедля нагревания 1кг газа на 1К при постоянном объёме).

Диффузия.

Заключается в том, что происходит самопроизвольное проникновение и перемешивание частиц двух соприкасающихся газов, жидкостей и твёрдых тел. Диффузия сводится к обмену масс частиц этихтел, возникает и продолжается пока существует градиент плотности.

Явление диффузии для химически однородного газа подчиняется закону Фика:

,

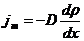где 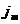-плотность потока массы – величина, определяемая массой вещества, диффундирующего за единицу времени через единичную площадку, перпенд-ную оси х, 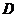-кооэффициент диффузии, 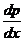-градиент плотности, равный скорости изменения плотности на единицу длины х в направлении нормали к этой площадке. Знак минус показывает, что перенос массы происходит в направлении убывания плотности (поэтому знак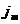и и 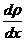противоположны). Диффузия 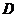численно равна плотностипотока массы при градиенте плотности, равном единице. Согласно кинетической теории газов:

.

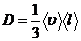Ответы к экзамену по физике.

1. Кинематика поступательного движения материальной точки. (путь, перемещение, скорость, ускорение).

Кинематика – изучает движение тел, не рассматривая причины, которые это движение обуславливает.

Мат.точка – не имеет размеров, но в мат.точке сосредоточенна масса всего тела.

Поступательное – движение при котором прямая связанная с телом остаётся || самой себе.

A = f(x,y,z)

r = f(t)

Кинетические ур-я движения мат.точки:

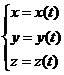
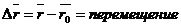
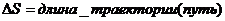
Траектория – линия описываемая мат.точкой в пространстве.

Перемещение – приращение радиуса-вектора точки за рассматриваемый промежуток времени.

Скорость – Быстрота движения мат.точки.

Вектором средней скорости< 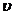> называется отношение приращения 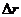радиуса-вектора точки к промежутку времени .

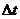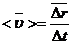
Мгновенная скорость – величина, равная первой производной радиуса-вектора движущейся точки по времени.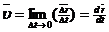

Модуль мгновенной скорости равен первой производной пути по времени.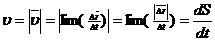

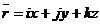
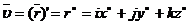
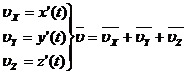Компоненты 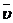равны производным от координат по времени.

Равномерное – движение при котором за равные промежутки времени тело проходит одинаковые пути.

Неравномерное – движение при котором скорость меняется как по модулю так и по направлению.

; ; ; ;

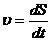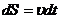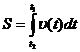2. Ускорение и его составляющие.

Ускорение – физ.величина, определяющая быстроту изменения скорости, как по модулю, так и по направлению.

Средним ускорением неравномерного движения в интервале времени от t до t+ 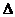t называется векторная величина равная отношению изменения скорости 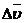к интервалу времени 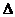t: .

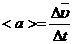Мгновенным ускорением 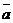мат.точки в момент времени t будет предел среднего ускорения. . .

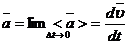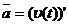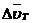определяет 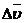по модулю.

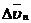определяет 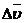по направлению.

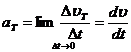, т.е. равна первой производной по времени от модуля скорости, определяя тем самым быстроту изменения скорости по модулю.

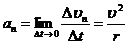, нормальная составляющая ускорения направлена по нормали к траектории к центру её кривизны (поэтому её также называют центростремительным ускорением).

Полное ускорение тела есть геометрическая сумма тангенциальной и нормальной составляющих.

Если а_н=?,а_т=?

3. 1,2,3 законы Ньютона.

В основе Динамики мат.точки лежат три закона Ньютона.

Первый закон Ньютона –всякая материальная точка (тело) сохраняет состояние покоя или равномерного прямолинейного движения до тех пор, пока воздействие со стороны других тел не заставит её изменить это состояние.

Инертность – стремление тела сохранять состояние покоя или равномерного прямолинейного движения.

Законы Ньютона выполняются только в инерциальной системе отсчёта.

Инерциальная система отсчёта – система, которая либо покоится, либо движется равномерно и прямолинейно относительно какой то другой инерциальной системы.

Масса тела – физ.величина, являющаяся одной из основных характеристик материи, определяющая её инерционные (инертная масса) и гравитационные (гравитационная масса) св-ва.

Сила – векторная величина, являющаяся мерой механического воздействия на тело со стороны других тел или полей, в результате которого тело приобретает ускорение или изменяет свою форму и размеры.

Обозначения(…)

Второй закон Ньютона – ускорение, приобретаемое материальной точкой (телом), пропорционально вызывающей его силе, совпадает с нею по направлению и обратно пропорционально массе материальной точки.

; ; ;

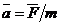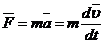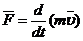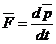
Импульс (кол-во движения) – векторная величина, численно равная произведению массы материальной точки на её скорость и имеющая направление скорости.

Более общая формулировка 2-го закона Н.(уравнение движения мт): скорость изменения импульса материальной точки равна действующей на неё силе.

Следствие из 2зН: принцип независимости действия сил: если на мт действует одновременно несколько сил, то каждая из этих сил сообщает мт ускорение согласно 2зН, как будто других сил не было.

Третий закон Ньютона. Всякое действие мт (тел) друг на друга, носит характер взаимодействия; силы, с которыми действуют друг на друга мт, всегда равны по модулю, противоположно направлены и действуют вдоль прямой, соединяющей эти точки.

4. Импульс тела, сила. Закон сохранения импульса.

Импульс (кол-во движения) – векторная величина, численно равная произведению массы материальной точки на её скорость и имеющая направление скорости.

Сила – векторная величина, являющаяся мерой механического воздействия на тело со стороны других тел или полей, в результате которого тело приобретает ускорение или изменяет свою форму и размеры.

Внутренние силы – силы взаимодействия между мт механической системы.

Внешние силы – силы, с которыми на мт системы действуют внешние тела.

Замкнутая – механическая система тел, на которую не действуют внешние силы.

В механической системе тел, по 3-му закону Ньютона, силы, действующие между этими телами, будут равны и противоположно направлены, т.е. геометрическая сумма внутренних сил равна 0.

Запишем 2зН, для каждого из n тел механической системы(мс):

…………………

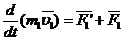
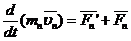
Сложим эти ур-я:

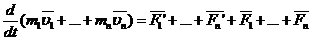
Т.к. геометрическая сумма внутренних сил мс по 3зН равна 0, то:

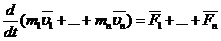
или:

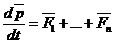
где 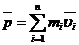- импульс системы.

В случае отсутствия внешних сил(замкнутая система):

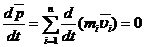, т.е.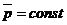

Это и есть закон сохранения импульса:импульс замкнутой системы сохраняется, т.е. не изменяется с течением времени.

5. Центр масс движение центра масс.

Центр масс (центр инерции) системы мт называется воображаемая точка С, положение которой характеризует распределение массы этой системы.

Радиус-вектор этой точки равен:

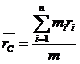
Скорость центра масс (цм):

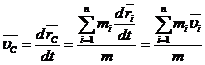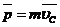; , т.е. импульс системы равен произведению массы системы на скорость её центра масс.

Т.к. 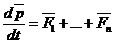то: 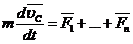, т.е.:

Закон движения центра масс: центр масс системы движется как мт, в которой сосредоточена масса всей системы и на которую действует сила, равная геометрической сумме всех внешних сил, действующих на систему.

6. Уравнение движения тела переменной массы.

Уравнение движения тела переменной массы (на примере ракеты):

Если в момент времени t масса ракеты m, а её скорость 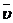, то по истечении времени dt её масса уменьшится на dm и станет равной m-dm, а скорость станет равной 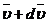. Изменение импульса системы за отрезок времени dt: 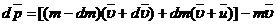, где u – скорость истечения газов, относительно ракеты. Отсюда: 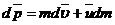(учли, что 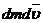- малый по сравнению с остальными).

Если на систему действуют внешние силы, то 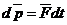: 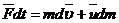, или: 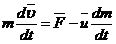, член 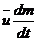- реактивная сила ( 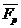), если 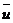противоположен 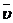, то ракета ускоряется, а если совпадает, тот тормозится, т.о.: уравнение движения тела переменной массы: .

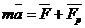Если на ракету не действуют внешние силы ( 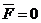), и u=const, то: 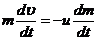, отсюда: 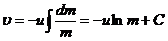, Если в начальный момент времени скорость равна 0, а масса равна m₀, то 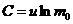, следовательно: 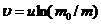. Это соотношение – Формула Циолковского, она показывает, что:

1) чем конечная масса (m), тем должна быть m₀.

2) чем u, тем может быть m при данной стартовой скорости.

7. Кинематика вращательного движения материальной точки.

Угловая скорость – векторная величина, равная первой производной угла поворота тела по времени.

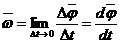
Вектор 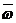направлен вдоль оси вращения по правилу правого винта.

Линейная скорость точки:

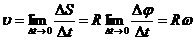
В векторном виде: 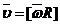, при этом модуль равен: .

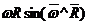Если 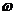=const, то вращение равномерное.

Период вращения (Т) – время, за которое точка совершает один полный оборот. ( ) .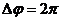

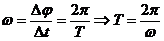Частота вращения (n) – число полных оборотов, совершаемых телом при равномерном его движении по окружности, в единицу времени. ; .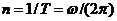

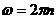Угловое ускорение – векторная величина, равная первой производной угловой скорости по времени: 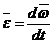. При ускоренном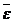 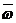, при замедленном .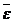

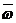Тангенциальная составляющая ускорения: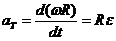

Нормальная составляющая: .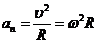

Формулы связи линейных и угловых величин:

, , , .

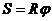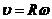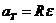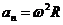При :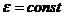

, .

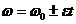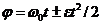8. Момент силы.

Момент силы F относительно неподвижной точки О называется физическая величина, определяемая векторным произведением радиуса-вектора r, проведённого из точки О в точку А приложения силы, на силу F.

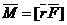, здесь 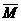- псевдовектор, его направление совпадает с направлением поступательного движения правого винта при его вращении от 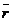к .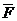

Модуль момента силы равен .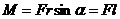

Момент силы относительно неподвижной оси z – скалярная величина 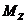, равная проекции на эту ось вектора 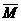момента силы, определённого относительно произвольной точки О данной оси z. Значение момента не зависит от выбора положения точки О на данной оси.

Момент инерции твёрдого тела. Теорема Штейнера.

Момент инерции системы (тела) относительно оси вращения называется физическая величина, равная сумме произведений масс n мт системы на квадрат их расстояний до рассматриваемой оси.

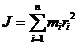, при непрерывном распределении масс: .

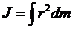Найдём момент инерции однородного сплошного цилиндра:

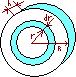
Разобьём цилиндр на отдельные полые концентрические цилиндры бесконечно малой толщины dr, с внутренним радиусом r и внешним – r+dr. Момент инерции каждого полого цилиндра – dJ=r²dm, где dm – масса всего элементарного цилиндра. Его объем - 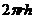dr.

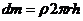dr, и 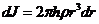. Тогда момент инерции всего цилиндра равен:

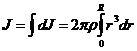
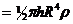, но т.к. 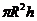-объём, то масса - 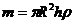, значит:

.

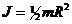Теорема Штейнера: момент инерции тела J относительно любой оси вращения равен моменту его инерции J_C относительно параллельной оси, проходящеё через центр масс С тела, сложе