Второй постулат: свет распространяется в вакууме с определенной скоростью с, не зависящей от скорости источника или наблюдателя.

Эти два постулата образуют основу теории относительности А. Эйнштейна.( 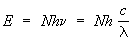)где ν — частота излучения, с — скорость света, λ— длина световой волны, h — постоянная Планка

58)Преобразования Лоренца

Лоренца преобразования, в специальной теории относительности — преобразования координат и времени какого-либо события при переходе от одной инерциальной системы отсчёта к другой. Получены в 1904 Х. А. Лоренцом как преобразования, по отношению к которым уравнения классической микроскопической электродинамики (Лоренца — Максвелла уравнения) сохраняют свой вид. В 1905 А.Эйнштейн вывел их, исходя из двух постулатов, составивших основу специальной теории относительности: равноправия всех инерциальных систем отсчёта и независимости скорости распространения света в вакууме от движения источника света.

Рассмотрим частный случай двух инерциальных систем отсчёта å и å’ с осями х и x’, лежащими на одной прямой, и соответственно параллельными другими осями (у и y’, z и z’). Если система å’ движется относительно å с постоянной скоростью u в направлении оси х, то Л. п. при переходе от å к å’ имеют вид:

,

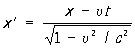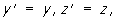
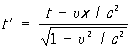
где с — скорость света в вакууме (штрихованные координаты относятся к системе å’, нештрихованные — к å).

Л. п. приводят к ряду важных следствий, в том числе к зависимости линейных размеров тел и промежутков времени от выбранной системы отсчёта, к закону сложения скоростей в теории относительности и др. При скоростях движения, малых по сравнению со скоростью света (u<<c), Л. п. переходят в преобразования Галилея (см. Галилея принцип относительности), справедливые в классической механике Ньютона.

59)Следствия из преобразований Лоренца

1. Если в одной системе отсчета некоторые события происходят в точках x₁ и x₂ в один и тот же момент времени t, то в другой системе отсчета эти события происходят в точках x'₁ и x'₂ в разные моменты времени t'₁ и t'₂:

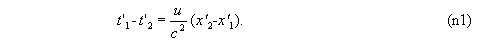
Понятие одновременности оказывается зависящим от выбора системы отсчета.

2. Если в одной системе отсчета между двумя событиями, происходящими в одной и той же точке, проходит время t, то в другой системе отсчета между этими же событиями проходит время

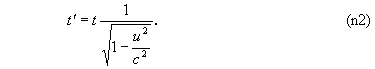
Это соотношение выражает релятивистский эффект замедления времени в движущихся объектах.

3. Если в одной системе отсчета покоящаяся линейка имеет длину l, то в системе отсчета, в которой линейка движется со скоростью u вдоль своей оси, ее длина

Этот эффект называется релятивистским сокращением продольных размеров тела. Поперечные размеры тела не изменяются при переходе в другие инерциальные системы отсчета.

4. Если в одной системе отсчета тело имеет скорость v= (v_x, v_y, v_z), то его скорость v' = (v'_x, v'_y, v'_z) в другой системе отсчета равна

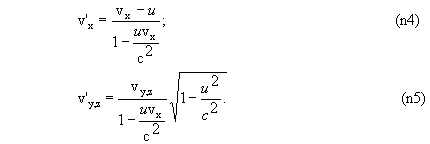
или в трехмерной векторной форме

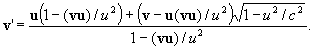
5. Из соотношений (n4), (n5) следует постоянство скорости c в различных системах отсчета. Действительно, если вычислить сумму квадратов левых частей этих равенств при условии

v²=(v_x)²+(v_y) ²+(v_z) ²=c², (n6)

получим

v'²=(v'_x)²+ (v'_y)²+(v'_z) ²=c². (n7)

Т. е. скорость c одинакова по величине во всех инерциальных системах отсчета (независимо от направления). Заметим, что направления скоростей v и v' в общем случае различны в разных системах отсчета.

60)Интервал между событиями

Согласно преобразованиям Лоренца (36.3),

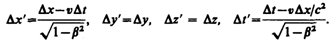
Подставив эти значения в (38.2), после элементарных преобразований получим, что 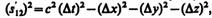т. е.

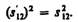
Обобщая полученные результаты, можно сделать вывод, что интервал, определяя пространственно-временные соотношения между событиями, является инвариантом при переходе от одной инерциальной системы отсчета к другой. Инвариантность интервала означает, что, несмотря на относительность длин и промежутков времени, течение событий носит объективный характер и не зависит от системы отсчета.

Теория относительности, таким образом, сформулировала новое представление о пространстве и времени. Пространственно-временные отношения являются не абсолютными величинами, как утверждала механика Галилея — Ньютона, а относительными. Следовательно, представления об абсолютном пространстве и времени являются несостоятельными. Кроме того, инвариантность интервала между двумя событиями свидетельствует о том, что пространство и время органически связаны между собой и образуют единую форму существования материи — пространство-время. Пространство и время не существуют вне материи и независимо от нее.

Дальнейшее развитие теории относительности (общая теория относительности, или теория тяготения) показало, что свойства пространства-времени в данной области определяются действующими в ней полями тяготения. При переходе к космическим масштабам геометрия пространства-времени не является евклидовой (т. е. не зависящей от размеров области пространства-времени), а изменяется от одной области к другой в зависимости от концентрации масс в этих областях и их движения.

61)Основной закон релятивистской динамики материальной точки

Масса движущихся релятивистских частиц зависит от их скорости:

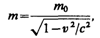(39.1)

где m₀ — масса покоя частицы, т. е. масса, измеренная в той инерциальной системе отсчета, относительно которой частица находится в покое; с — скорость света в ваку­уме; т — масса частицы в системе отсчета, относительно которой она движется со скоростью v. Следовательно, масса одной и той же частицы различна в разных инерциальных системах отсчета.

Из принципа относительности Эйнштейна, утверждающего инвариантность всех законов природы при переходе от одной инерциальной системы отсчета к другой, следует условие инвариантности уравнений физических законов относительно преобразований Лоренца. Основной закон динамики Ньютона

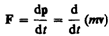
оказывается также инвариантным по отношению к преобразованиям Лоренца, если в нем справа стоит производная по времени от релятивистского импульса.

Основной закон релятивистской динамики материальной точки имеет вид

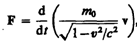(39.2)

или

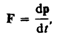(39.3)

где

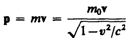(39.4)

— релятивистский импульс материальной точки.

Отметим, что уравнение (39.3) внешне совпадает с основным уравнением ньютоновской механики (6.7). Однако физический смысл его другой: справа стоит производ­ная по времени от релятивистского импульса, определяемого формулой (39.4). Таким образом, уравнение (39.2) инвариантно по отношению к преобразованиям Лоренца и, следовательно, удовлетворяет принципу относительности Эйнштейна. Следует учиты­вать, что ни импульс, ни сила не являются инвариантными величинами. Более того, в общем случае ускорение не совпадает по направлению с силой.

В силу однородности пространства в релятивистской механике выполняет­сязакон сохранения релятивистского импульса: релятивистский импульс замкнутой системы сохраняется, т. е. не изменяется с течением времени. Часто вообще не оговаривают, что рассматривают релятивистский импульс, так как если тела движутся со скоростями, близкими к с, то можно использовать только релятивистское выраже­ние для импульса.

Анализ формул (39.1), (39.4) и (39.2) показывает, что при скоростях, значительно меньших скорости с, уравнение (39.2) переходит в основной закон (см. (6.5)) классичес­кой механики. Следовательно, условием применимости законов классической (ньютоновской) механики является условие v<<c. Законы классической механики получаются как следствие теории относительности для предельного случая v<<c (формально пере­ход осуществляется при с®¥). Таким образом,классическая механика — это механика макротел, движущихся с малыми скоростями (по сравнению со скоростью света в вакууме).

Экспериментальное доказательство зависимости массы от скорости (39.1) является подтверждением справедливости специальной теории относительности. В дальнейшем будет показано, что на основании этой зависимости производятся расчеты ускорителей.