В замкнутой системе геометрическая сумма импульсов тел остается постоянной при любых взаимодействиях тел этой системы между собой.

Этот фундаментальный закон природы называется законом сохранения импульса.

Необходимым условием применимости закона сохранения импульса к системе взаимодействующих тел является использование инерциальной системы отсчета.

27)Центр масс

Центр масс, центр инерции, геометрическая точка, положение которой характеризует распределение масс в теле или механической системе. Координаты Ц. м. определяются формулами

, ,

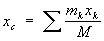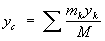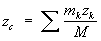
или для тела при непрерывном распределении масс

, ,

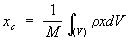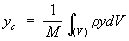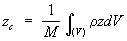
где m_к — массы материальных точек, образующих систему, x_k, у_к, z_k — координаты этих точек, М =Sm_к —масса системы, r — плотность, V — объём. Понятие о Ц. м. отличается от понятия о центре тяжести тем, что последнее имеет смысл только для твёрдого тела, находящегося в однородном поле тяжести; понятие же о Ц. м. не связано ни с каким силовым полем и имеет смысл для любой механической системы. Для твёрдого тела положения Ц. м. и центра тяжести совпадают.

При движении механической системы её Ц. м. движется так, как двигалась бы материальная точка, имеющая массу, равную массе системы, и находящаяся под действием всех внешних сил, приложенных к системе. Кроме того, некоторые уравнения движения механической системы (тела) по отношению к осям, имеющим начало в Ц. м. и движущимся вместе с Ц. м. поступательно, сохраняют тот же вид, что и для движения по отношению к инерциальной системе отсчёта. Ввиду этих свойств понятие о Ц. м. играет важную роль в динамике системы и твёрдого тела.

28)Закон движения центра масс

Если главный вектоp внешних сил остается все вpемяpавным нулю, то центp масс механической системы находится в покое или движется пpямолинейно и pавномеpно.

Рассмотрим некоторые примеры.

1. Пpи полете снаpяда единственной внешней силой является сила тяжес-ти (вес), если пpенебpечьсопpотивлением воздуха, поэтому центp масс снаpяда движется как матеpиальная точка под действием силы тяжести, т.е. по паpабо-ле. Если в полете снаpядpазоpвется, то действующие пpивзpыве силы (внутренние) не могут изменить движение центpа масс снаpяда.

2. Пpедставим себе человека, стоящего на совеpшенно гладкой плоскос-ти. Внешними силами являются вес человека и ноpмальнаяpеакцияповеpхнос-ти. Они могут пеpеместитьцентp тяжести человека по веpтикали. Гоpизонталь-ныепеpемещенияцентpа тяжести человека невозможны, следовательно, хождение по идеально гладкому льду невозможно. Точно также движение автомобиля или локомотива возможно только благодаpя наличию сил тpения.

Количество движения точки и системы. Количеством движения матеpиальной точки называется вектоp, имеющий напpавлениевектоpаскоpости и модуль, pавный произведению массы точки m на модуль скоpости ее движения V, и напpавлен по направлению скоpости, по касательной к тpаектоpии движения.
Количество движения является мерой меха Единицей количества движения в системе СИ является 1 кг 1 м/сек = 1кгм/с. Г л а в н ы м в е к т о p о м количества движения системы называется геометpическая сумма количеств движения матеpиальных точек входящих в систему

Так как производная от суммы равна сумме производных, то из выражения следует, что

Этот вектоp не имеет точки пpиложения, он является вектоpноймеpой механического движения системы.

29)Момент Инерции

Момент инерции

(Momentd'inertie, Trägheitsmoment, Momentofinertia) - понятие это введено в науку Эйлером, хотя уже Гюйгенс раньше пользовался выражением того же рода, не давая ему особого названия: один из путей, приводящий к его определению, следующий. Положим, что каждая частица системы имеет массу т и все они движутся прямолинейно, со скоростью v, общей для всех частиц как по величине, так и по направлению; тогда живая сила W такой системы выразится уравнением:

W = 1/2∑mv² = 1/2Mv²,

так как сумма масс всех частиц системы равна М, массе всей системы. Когда же твердое тело или вообще неизменяемая система вращается около неподвижной оси, дело сложнее: однаугловая скорость, w, будет общая для всех частичек системы, линейные же скорости каждой из них будут иметь мерой произведение ее кратчайшего расстояния r от общей оси вращения на общую угловую скорость w. Для такого случая живая сила всей системы будет

W₁ = 1/2∑mr₂∙w₂ = 1/2Jw².

Здесь величина: J = ∑mr2, так наз. "М. инерции" относительно данной оси, заменяет коэффициент М, так наз. массу в выражении живой силы при прямолинейном движении с общей скоростью v, и служит мерой инерции при вращательном движении. Выражения такого же вида получаются и при рассмотрении иных вопросов: например в учении о сопротивлении строительных материалов излому (см.); поэтому-то определение М. инерции для тел разной формы неоднократно занимало математиков. Так как сумма масс всех частиц тела всегда равна его массе М, то М. инерции часто находят удобным выражать в виде произведения массы тела М на квадрат некоторой чисто геометрической величины К линейного измерения [измерение же М. ин.будет (l², m, t⁰) в системе абсолютных мер]

∑mv² = MK², или: K² = (∑mr²)/M.

30)Теорема Штейнера

Теоре́маШте́йнера: момент инерции тела I относительно произвольной оси равен сумме момента инерции этого тела I^c относительно оси, проходящей через центр масс тела параллельно рассматриваемой оси, и произведения массы тела m на квадрат расстояния d между осями:

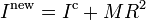
где

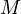— масса тела, и

R — расстояние между осями.

31)Кинетическая энергия вращательного движения

Кинетическая энергия тела, движущегося произвольным образом, равна сумме кинетических энергий всех n материальных точек па которые это тело можно разбить:

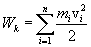
Если тело вращается вокруг неподвижной оси с угловой скоростью 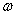, то линейная скорость i-ой точки равна 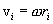, где 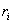, - расстояние от этой точки до оси вращения. Следовательно.

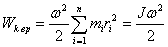(5.11)

где 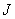- момент инерции тела относительно оси вращения.

В общем случае движение твердого тела можно представить в виде суммы двух движений - поступательного со скоростью, равной скорости 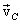центра инерции тела, и вращения с угловой скоростью 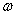вокруг мгновенной оси, проходящей через центр инерции. При этом выражение для кинетической энергии тела преобразуется к виду

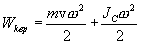(5.12)

где 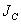- момент инерции тела относительно мгновенной оси вращения, проходящей через центр инерции.

32)Момент силы

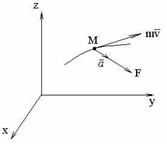
Итак, для равновесия тела, закрепленного на оси, существенна не сама величина силы, а произведение проекции силы на направление, перпендикулярное к радиусу, проведенному к точке приложения силы, на расстояние этой точки от оси. Это произведение будем называть моментом силы относительно данной оси или просто моментом силы (рис. 116). Моменты разных сил, приложенных к одной точке, равны, если равны проекции этих сил на направление, перпендикулярное к радиусу данной точки (рис. 117).

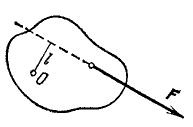
Рис. 116. Момент силы F paвен произведению ее проекции F\' на расстояние r.

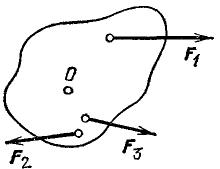
Рис. 117. Силы F, F₁, F₂ и F₃ имеют одинаковые моменты отноcительно оси О.

Условимся считать момент силы положительным, если эта сила, действуя в отдельности, вращала бы тело по часовой стрелке, и отрицательным в противоположном случае (при этом нужно заранее условиться, с какой стороны мы будем смотреть на тело). Например, согласно рис. 118, силам F₁ и F₂ следует приписать положительный момент, а силе F₃— отрицательный.

Моменту силы можно дать еще и другое определение. Момент силы F на рис. 119 есть M=rF\'. Опустим перпендикуляр d из точки О на направление силы. Прямоугольные треугольники на чертеже подобны, ибо их соответственные углы равны. Следовательно,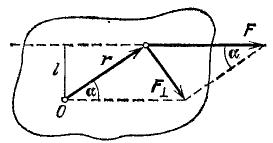

Рис. 118. Моменты сил F₁ и F₂ положительны, момент силы F₃ отрицателен.

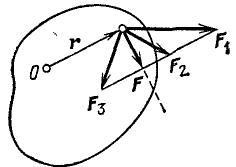
Рис. 119. Момент силы можно выразить через силу и плечо силы, M=Fd.

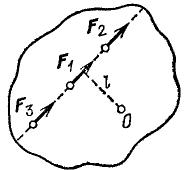
Рис. 120. Равные силы F₁, F₂, F₃ с одинаковым плечом d имеют равные моменты относительно оси О.

Следовательно, M=Fd, т. е. момент силы равен произведению силы F на длину перпендикуляра d, опущенного из оси на направление силы.

Длину перпендикуляра, опущенного из оси на направление силы, называют плечом силы. Значит, момент силы равен произведению величины силы на плечо силы. Ясно, что перенесение точки приложения силы вдоль ее направления не меняет ее момента (рис. 120). Если направление силы проходит через ось вращения, то плечо силы равно нулю; следовательно, равен нулю и момент силы этом случае сила не вызывает вращения тела: сила, момент которой относительно данной оси равен нулю, не вызывает вращения вокруг этой оси.

Пользуясь понятием момента силы, мы можем по-новому сформулировать условия равновесия тела, закрепленного на оси и находящегося под действием двух сил. Как мы видели, для равновесия необходимо, чтобы силы стремились вращать тело в противоположных направлениях и чтобы произведения сил на их расстояния до оси были равны. Значит, при равновесии моменты обеих сил должны быть равны по величине и противоположны по знаку. Таким образом, для равновесия тела, закрепленного на оси, алгебраическая сумма моментов действующих на него сил должна быть равна нулю.

Так как момент силы определяется произведением величины силы на плечо, то единицу момента мы получим, взяв силу, равную единице, плечо которой также равно единице. Значит, в системе СИ единицей момента силы является момент силы в 1 н, действующей на плече в 1 м, т. е. 1 н*м, в системе СГС —1 дин*см, в системе МКСС— 1 кГ*м. Пользуясь данными § 45, найдем соотношения между этими единицами:

1 дин*см = 10^-7 н*м; 1 кГ*м = 9,8 н*м.

Если на тело, закрепленное на оси, действует много сил, то, как показывает опыт, условие равновесия остается тем же, что и для случая двух сил: для равновесия тела, закрепленного на оси, алгебраическая сумма моментов всех сил, действующих на тело, должна быть равна нулю.

Можно ввести понятие об уравновешивающем моменте, о равнодействующем моменте и о сложении моментов сил, действующих на тело, закрепленное на оси, подобно тому как были введены понятия об уравновешивающей силе, о равнодействующей силе и о сложении сил. Так, результирующим моментом нескольких моментов, действующих на тело (составляющих моментов), будем называть алгебраическую сумму составляющих моментов. Под действием результирующего момента тело будет двигаться (вращаться вокруг оси) так же, как оно вращалось бы при одновременном действии всех составляющих моментов. В частности, если результирующий момент равен нулю, то тело, закрепленное на оси, либо покоится, либо вращается равномерно.

33)Уравнение динамики вращательного движения твердого тела

Согласно уравнению (5.8) второй закон Ньютона для вращательного движения

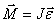
По определению угловое ускорение 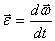и тогда это уравнение можно

переписать следующим образом

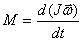
с учетом (5.9)

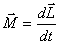
или

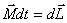(5.10)

Это выражение носит название основного уравнения динамики вращательного движения и формулируется следующим образом: изменение момента количества движения твердого тела 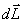, равно импульсу момента 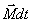всех внешних сил, действующих на это тело.

34)Момент импульса

Моме́нти́мпульса -характеризует количествовращательного движения. Величина, зависящая от того, сколько массы вращается, как она распределена относительно оси вращения и с какой скоростью происходит вращение.

Следует учесть, что вращение здесь понимается в широком смысле, не только как регулярное вращение вокруг оси. Например, даже при прямолинейном движении тела мимо произвольной воображаемой точки, не лежащей на линии движения, оно также обладает моментом импульса. Наибольшую, пожалуй, роль момент импульса играет при описании собственно вращательного движения. Однако крайне важен и для гораздо более широкого класса задач (особенно — если в задаче есть центральная или осевая симметрия, но не только в этих случаях).

Момент импульса 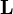материальной точки относительно некоторого начала отсчёта определяется векторным произведением её радиус-вектора иимпульса:

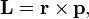
где 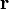— радиус-вектор частицы относительно выбранного неподвижного в данной системе отсчёта начала отсчёта, 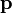— импульс частицы.

Для нескольких частиц момент импульса определяется как (векторная) сумма таких членов:

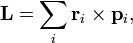
где 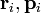— радиус-вектор и импульс каждой частицы, входящей в систему, момент импульса которой определяется.

(В пределе количество частиц может быть бесконечным, например, в случае твердого тела с непрерывно распределенной массой или вообще распределенной системы это может быть записано как 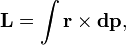где 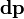— импульс бесконечно малого точечного элемента системы).

В системе СИ момент импульса измеряется в единицах джоуль-секунда; Дж·с.

Из определения момента импульса следует его аддитивность: как, для системы частиц в частности, так и для системы, состоящей из нескольких подсистем, выполняется:

.

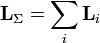· Замечание: в принципе момент импульса может быть вычислен относительно любого начала отсчета (получившиеся при этом разные значения связаны очевидным образом); однако чаще всего (для удобства и определенности) его вычисляют относительно центра масс или закрепленной точки вращения твердого тела итп).

35)Закон сохранения момента импульса

Зако́нсохране́ниямоме́нтаи́мпульса (закон сохранения углового момента) — один из фундаментальных законов сохранения. Математически выражается через векторную сумму всех моментов импульса относительно выбранной оси для замкнутой системы тел и остается постоянной, пока на систему не воздействуют внешние силы. В соответствии с этиммомент импульса замкнутой системы в любой системе координат не изменяется со временем.

Закон сохранения момента импульса есть проявление изотропности пространства относительно поворота.

В упрощённом виде: ΣL(вектор)=const ,если система находится в равновесии.

36)Деформации твердого тела

Виды деформаций. Деформацией называют изменение формы, размеров тела. Деформация может быть вызвана действием на тело приложенных к нему внешних сил.

Деформации, полностью исчезающие после прекращения действия на тело внешних сил, называют упругими, а деформации, сохраняющиеся и после того, как внешние силы перестали действовать на тело, – пластическими.

Различают деформации растяжения и сжатия (одностороннего и всестороннего), изгиба, кручения и сдвига.

Силы упругости.При деформациях твердого тела его частицы (атомы, молекулы, ионы), находящиеся в узлах кристаллической решетки, смещаются из своих положений равновесия. Этому смещению противодействуют силы взаимодействия между частицами твердого тела, удерживающие эти частицы на определенном расстоянии друг от друга. Поэтому при любом виде упругой деформации в теле возникают внутренние силы, препятствующие его деформации.

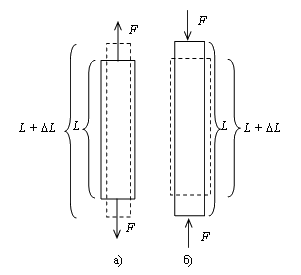Рис. 5.11.Деформация растяжения (а) и сжатия (б)

Силы, возникающие в теле при его упругой деформации и направленные против направления смещения частиц тела, вызываемого деформацией, называют силами упругости. Силы упругости действуют в любом сечении деформированного тела, а также в месте его контакта с телом, вызывающим деформации. В случае одностороннего растяжения или сжатия сила упругости направлена вдоль прямой, по которой действует внешняя сила, вызывающая деформацию тела, противоположно направлению этой силы и перпендикулярно поверхности тела.

Рассмотрим простейшую деформацию продольного растяжения или одностороннего сжатия. Представим себе однородный стержень длины L, с площадью поперечного сечения S, к концам которого приложены силы F, в результате чего длина стержня меняется на величину ΔL. Для характеристики деформации растяжения существенно не абсолютное значение удлинения стержня ΔL, а относительное удлинение .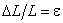

Растягивающие силы считаем положительными; в этом случае (рис. 5.11а) ΔL тоже положительно, поскольку при растяжении длина стержня увеличивается. Сжимающие силы считаем отрицательными; в этом случае (рис. 5.11б) ΔL отрицательно; это означает, что, когда стержень подвергается одностороннему сжатию, его длина L уменьшается.

Эксперименты свидетельствуют, что относительная деформация тем больше, чем больше действующая сила и чем меньше поперечное сечение стержня. Этот результат можно представить в виде математического соотношения

.

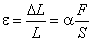(5.1)

Величина 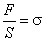называется механическим напряжением или просто напряжением. С учетом этого выражение (5.1) принимает вид

,

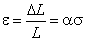(5.2)

где коэффициент α, носящий название коэффициента упругости, зависит только от материала, из которого сделан стержень.

Наряду с коэффициентом упругости α материал принято характеризовать обратной величиной:

,

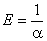(5.3)

которую называют модулем упругости, или модулем Юнга. Подставляя в (5.2) (5.3) получаем:

.

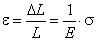(5.4)

Из выражения (5.4) находим:

.

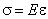37)Энергия

Эне́ргия (др.-греч. ἐνέργεια — «действие, деятельность, сила, мощь») — скалярная физическая величина, являющаяся единой мерой различных форм движения и взаимодействия материи, мерой перехода движения материи из одних форм в другие. Введение понятия энергии удобно тем, что в случае, если физическая система является замкнутой, то её энергия сохраняется во времени. Это утверждение носит название закона сохранения энергии. Понятие введено Аристотелем в трактате «Физика».

С фундаментальной точки зрения энергия представляет собой интеграл движения (то есть сохраняющуюся при движении величину), связанный, согласно теореме Нётер, с однородностью времени. Таким образом, введение понятия энергии как физической величины целесообразно только в том случае, если рассматриваемая физическая система однородна во времени.

Физическая размерность

Энергия E имеет размерность, равную:

Описание	Формула
Силе, умноженной на длину	E ~ F·l
Давлению, умноженному на объём	E ~ P·V
Импульсу, умноженному на скорость	E ~ p·v
Массе, умноженной на квадрат скорости	E ~ m·v²
Заряду, умноженному на напряжение	E ~ q·U
Мощности, умноженной на время	E ~ N·t

Энергия и масса

Основная статья: Эквивалентность массы и энергии

Согласно специальной теории относительности между массой и энергией существует связь, выражаемая знаменитой формулой Эйнштейна

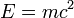
где E — энергия системы, m — её масса, c — скорость света. Несмотря на то, что исторически предпринимались попытки трактовать это выражение как полную эквивалентность понятия энергии и массы, что, в частности, привело к появлению такого понятия как релятивистская масса, в современной физике принято сужать смысл этого уравнения, понимая под массой массу тела в состоянии покоя (так называемая масса покоя), а под энергией — только внутреннюю энергию, заключённую в системе.

Энергия тела, согласно законам классической механики, зависит от системы отсчета, то есть неодинакова для разных наблюдателей. Если тело движется со скоростью v относительно некоего наблюдателя, то для другого наблюдателя, движущегося с той же скоростью, оно будет казаться неподвижным. Соответственно, для первого наблюдателя кинетическая энергия тела будет равна, 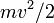, где m — масса тела, а для другого наблюдателя — нулю.

Эта зависимость энергии от системы отсчета сохраняется также в теории относительности. Для определения преобразований, происходящих с энергией при переходе от одной инерциальной системы отсчета к другой используется сложная математическая конструкция — тензор энергии-импульса.

Зависимость энергии тела от скорости рассматривается уже не так, как в ньютоновской физике, а согласно вышеназванной формуле Эйнштейна:

,

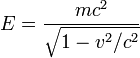где 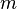— инвариантная масса. В системе отсчета, связанной с телом, его скорость равна нулю, а энергия, которую называют энергией покоя, выражается формулой:

.

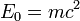Это минимальная энергия, которую может иметь массивное тело. Значение формулы Эйнштейна также в том, что до неё энергия определялась с точностью до произвольной постоянной, а формула Эйнштейна находит абсолютное значение этой постоянной.

38)Работа – в лекции

Работа есть физическая величина, численно равная произведению силы на перемещение в направлении действия этой силы и ей же вызванное.
Соответственно формула A = F*s. Если перемещение по направлению не совпадает с направлением действия силы, то появляется косинус угла.

39)Мощность

Мо́щность — физическая величина, равная в общем случае скорости изменения энергии системы. В более узком смысле мощность равна отношениюработы, выполняемой за некоторый промежуток времени, к этому промежутку времени.

Различают среднюю мощность за промежуток времени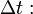

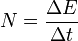
и мгновенную мощность в данный момент времени:

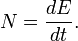
Интеграл от мгновенной мощности за промежуток времени равен полной переданной энергии за это время:

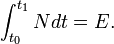
Если на движущееся тело действует сила, то эта сила совершает работу. Мощность в этом случае равна скалярному произведению вектора силы на вектор скорости, с которой движется тело:

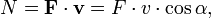где F — сила, v — скорость, 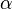— угол между вектором скорости и силы.

Частный случай мощности при вращательном движении:

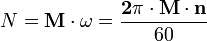M — момент силы, 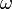— угловая скорость, 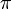— число пи, n — частота вращения (число оборотов в минуту, об/мин.).

40)Кинетическая энергия

Кинети́ческаяэне́ргия — энергия механической системы, зависящая от скоростей движения её точек. Часто выделяют кинетическую энергию поступательного и вращательного движения. Единица измерения в системе СИ — Джоуль.

Более строго, кинетическая энергия есть разность между полной энергией системы и её энергией покоя; таким образом, кинетическая энергия — часть полной энергии, обусловленная движением.

Рассмотрим систему, состоящую из одной частицы, и запишем уравнение движения:

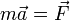
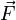— есть результирующая всех сил, действующих на тело. Скалярно умножим уравнение на перемещениечастицы 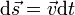. Учитывая, что 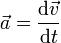, Получим:

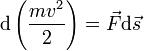
Если система замкнута, то есть 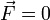, то 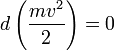, а величина

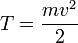
остаётся постоянной. Эта величина называется кинетической энергией частицы. Если система изолирована, то кинетическая энергия является интегралом движения.

Для абсолютно твёрдого тела полную кинетическую энергию можно записать в виде суммы кинетической энергии поступательного и вращательного движения:

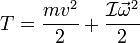
где:

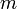— масса тела

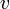— скорость центра масс тела

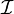— момент инерции тела

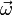— угловая скорость тела.

41)Теорема о кинетической энергии