Флуктуации. Распределение Гаусса. Влияние флуктуаций на предельную погрешность измерительных приборов.
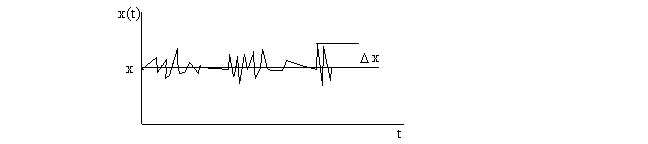
Мы уже отмечали, что замкнутая система наибольшую часть времени проводит в состоянии с энергией, близкой к наиболее вероятной Ев. Однако в силу конечной ширины DЕ возможно обнаружить систему и в других состояниях с энергиями, отличающимися от Ев . Следовательно, мгновенное значение энергии и других макропараметров системы (любой из них обозначим за х) будут испытывать самопроизвольные, случайные отклонения от средних величин - флуктуации. Флуктуации, иначе, есть самопроизвольные переходы из равновесного состояния в неравновесное. Пусть макропараметр со временем меняется по некоторому закону, см.рисунок. Рассчитаем вероятность флуктуации 
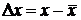
макропараметра х для замкнутой системы. Вероятность обнаружить систему в состоянии с энергией Е, в соответствии с микроканоническим распределением Гиббса (Р(Е) ~DГ) и определением энтропии S = klnDГ, запишется в виде
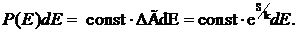
Для вероятности флуктуации параметра Dх запишем
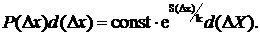(42.1)
где S (Dx) есть энтропийная функция в зависимости от параметра 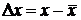. Разложим S(Dx) по степеням Dх, считая, что Dх мало, это позволит нам ограничиться тремя членами разложения
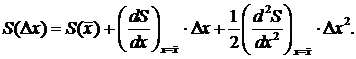(42.2)
В замкнутой равновесной системе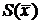 
постоянна и максимальна (состояние равновесия).
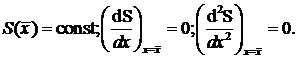
Тогда уравнение (42.2) сводится к виду:
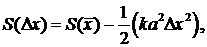(42.3)
где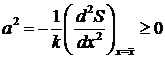 
всегда.
Подставляя (42.3) в (42.1), находим искомую вероятность
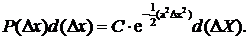(42.4)
Коэффициент Cопределяется из условия нормировки вероятности;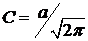 
. Таким образом, нормированная плотность вероятностей флуктуации Dх, известная под названием закона нормального распределения или распределения Гаусса, имеет вид
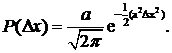(42.5)
В соответствии с (42.5) вероятность определяется квадратом флуктуации Dx, следовательно, не зависит от ее знака. Флуктуации, одинаковые по величине, но противоположные по знаку, равновероятны, поэтому среднее значение флуктуации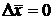 
. Вероятность больших флуктуаций чрезвычайно мала.
Флуктуации принято характеризовать среднеквадратичной величиной - дисперсией
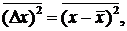
которая, очевидно, отлична от нуля и всегда положительна. Используя распределение Гаусса, находим
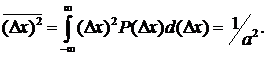
Очевидно, таким образом, что среднеквадратичная флуктуация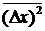 
(дисперсия) является основным параметром распределения Гаусса, она характеризует скорость уменьшения вероятности P(Dx) по мере увеличения флуктуации Dх. Чем меньше 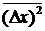, тем меньше вероятность больших флуктуаций.
Кроме дисперсии 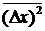, используют часто понятие относительной флуктуации
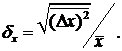(42.6)
В статистической физике доказывается, что относительная флуктуация - аддитивная величина и она обратно пропорциональна корню квадратному из числа N образующих систему тел (молекул и т.д.)
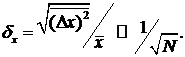(42.7)
Отсюда видно, что чем больше система, тем меньше относительные флуктуации макропараметров в ней. Следовательно, для больших макросистем рассчитанные методами статистической физики средние значения макровеличин с высокой точностью совпадают с наблюдаемым значением этих величин. Предсказание статистической физики тем достовернее, чем больше изучаемые системы.
Всегда имеющиеся флуктуации обуславливают предельную, принципиально неустранимую погрешность измерительных приборов. В качестве примера оценим наименьшую, неустранимую погрешность газового термометра - трубки с газом из N молекул, где указателем служит подвижная, например, жидкостная пробка. Абсолютная флуктуация показаний такого прибора в соответствии с (42.6), (42.7) есть
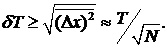
Т.е. термометр “почувствует” лишь такое изменение температуры dТ, которое больше среднестатической флуктуации.
Если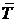 
= 300 К, N = 1020 ( объем V = 3.7 см3), то dТ > 3 10-8 К. Меньшие изменения температуры рассматриваемым прибором измерить невозможно.