Распределение Больцмана. Барометрическая формула.

Рассмотрим модель идеального газа. Применим к частице идеального газа каноническое распределение Гиббса в форме

(38.1)

Поставим задачей найти вероятность обнаружения частицы в присутствии внешнего потенциального поля в любом микросостоянии с импульсами в интервалах р_х¸ р_х + dр_х ; р_у¸ р_у + dр_у ; p_z¸ p_z + dp_z ; и с координатами в интервалах х ¸ х + dх ; у ¸ у + dу; z ¸ z + dz ; Тогда распределение (38.1) сводится к виду

(38.2)

здесь e = e(р_х,р_у,р_z, х,у,z) есть сумма кинетической энергии поступательного движения и потенциальной энергии частицы; e = e_к(р_х,р_у,р_z) + e_п (х,у,z); e_к = (р_х² + р_у² + р_z²)/2m ; потенциальная энергия 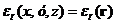, предполагается определенной в каждой точке пространства с радиус-вектором r = xe_x + уe_у + ze_z. Коэффициент с находится из условия нормировки.

Распределение (38.2) называют распределением Больцмана или, иногда, распределением Максвелла-Больцмана. Последнее название связано с тем, что распределение (38.2) можно представить в виде произведений двух множителей

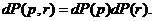(38.3)

где

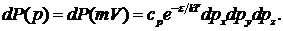(38.4)

Выражение (38.4) - одна из форм записи уравнений Максвелла. Если e_п = 0 во всех точках пространства, то распределение (38.2) переходит в распределение Максвелла. Второй множитель

(38.5)

описывает вероятность обнаружения частицы в элементарном объеме dV = dxdуdz в окрестностях точки с координатойr где потенциальная энергия составляет e_п(r). Если плотность частиц в состоянии с нулевой потенциальной энергией (e_п = 0) есть n_о(0), то в объеме dV в среднем будет находится

(38.6)

частиц.

Локальная плотность частиц в состояниях с энергией e_п составит

(38.7)

Это выражение носит название формулы Больцмана; оно справедливо для потенциальных полей любой физической природы. На рисунке показаны зависимости плотности распределения n_o(e_п) от энергии e_п для двух температур.

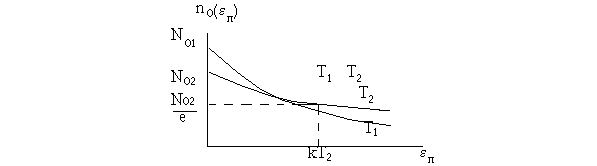
Формула Больцмана как распределение частиц по потенциальным энергиям отражает единство двух противоположностей. Под действием сил потенциального поля 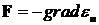частицы стремятся в состояние с минимальной энергией (принцип Ле-Шателье), но этому препятствует тепловое движение молекул, устанавливающее равновесие. Поэтому формула Больцмана, как и Максвелла, отражает подвижное, динамическое равновесие; оценки средних с использованием этих соотношений имеют среднестатистический, вероятностный характер.

Частным видом потенциального поля является поле силы тяжести, для него e_п(h)= mgh (h - высота над уровнем моря). Подставляя e_п(h) в (40.7) , сразу находим плотность распределения молекул воздуха по высоте.

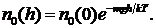(38.8)

Здесь n_о(0) - плотность молекул при h = 0, т.е. на уровне моря. От ( 38.8) сразу перейдем к давлению р(h) = n_o(h)kT , т.е. к барометрической формуле

(38.9)

Давление газа в поле силы тяжести меняется по экспоненциальному закону в зависимости от высоты и уменьшается в e раз при поднятии на характеристическую высоту h_o = kT/mg (для атмосферы Земли h_о @ 10 км). Барометрическая формула в реальных условиях дает приближенный результат: она не учитывает зависимости температуры воздуха и ускорения от высоты.