Уравнение Менделеева — Клапейрона

Берём формулу 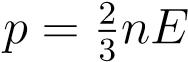и подставляем в неё 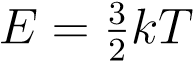. Получаем:

p = nkT.

Вспомним теперь, что 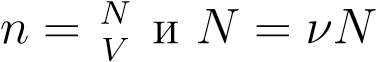_A, где ν — число молей газа:

,

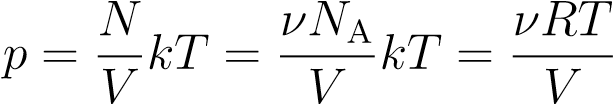откуда

pV = νRT. (3)

Соотношение (3) называется уравнением Менделеева — Клапейрона. Оно даёт взаимосвязь трёх важнейших макроскопических параметров, описывающих состояние идеального газа — давления, объёма и температуры. Поэтому уравнение Менделеева — Клапейрона называется ещё уравнением состояния идеального газа.

Учитывая, что 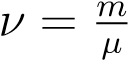, где m — масса газа, получим другую форму уравнения Менделеева — Клапейрона:

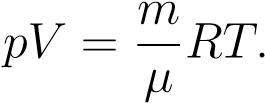(4)

Есть ещё один полезный вариант этого уравнения. Поделим обе части на V :

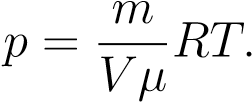
Но 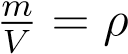— плотность газа. Отсюда

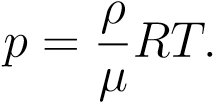(5)

В задачах по физике активно используются все три формы записи (3)—(5).

Изопроцессы

На протяжении этого раздела мы будем придерживаться следующего предположения: масса и химический состав газа остаются неизменными. Иными словами, мы считаем, что:

• m = const, то есть нет утечки газа из сосуда или, наоборот, притока газа в сосуд;

• µ = const, то есть частицы газа не испытывают каких-либо изменений (скажем, отсутствует диссоциация — распад молекул на атомы).

Эти два условия выполняются в очень многих физически интересных ситуациях (например, в простых моделях тепловых двигателей) и потому вполне заслуживают отдельного рассмотрения.

Если масса газа и его молярная масса фиксированы, то состояние газа определяется тремя макроскопическими параметрами: давлением, объёмом и температурой. Эти параметры связаны друг с другом уравнением состояния (уравнением Менделеева — Клапейрона).

Термодинамический процесс

Термодинамический процесс (или просто процесс) — это изменение состояния газа с течением времени. В ходе термодинамического процесса меняются значения макроскопических параметров — давления, объёма и температуры.

Особый интерес представляют изопроцессы — термодинамические процессы, в которых значение одного из макроскопических параметров остаётся неизменным. Поочерёдно фиксируя каждый из трёх параметров, мы получим три вида изопроцессов.

1. Изотермический процесс идёт при постоянной температуре газа: T = const.

2. Изобарный процесс идёт при постоянном давлении газа: p = const.

3. Изохорный процесс идёт при постоянном объёме газа: V = const.

Изопроцессы описываются очень простыми законами Бойля — Мариотта, Гей-Люссака и Шарля. Давайте перейдём к их изучению.

Изотермический процесс

При изотермическом процессе температура газа постоянна. В ходе процесса меняются только давление газа и его объём.

Установим связь между давлением p и объёмом V газа в изотермическом процессе. Пусть температура газа равна T. Рассмотрим два произвольных состояния газа: в одном из них значения макроскопических параметров равны p₁,V₁,T, а во втором — p₂,V₂,T. Эти значения связаны уравнением Менделеева — Клапейрона:

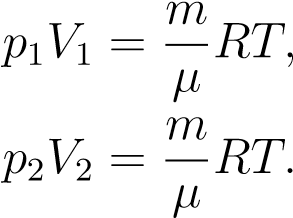
Как мы сказали с самого начала, масса газа m и его молярная масса µ предполагаются неизменными. Поэтому правые части выписанных уравнений равны. Следовательно, равны и левые части: p1V1 = p2V2.

Поскольку два состояния газа были выбраны произвольно, мы можем заключить, что в ходе изотермического процесса произведение давления газа на его объём остаётся постоянным:

pV = const.

Данное утверждение называется законом Бойля — Мариотта. Записав закон Бойля — Мариотта в виде

const

p = ,

V

можно дать и такую формулировку: в изотермическом процессе давление газа обратно пропорционально его объёму. Если, например, при изотермическом расширении газа его объём увеличивается в три раза, то давление газа при этом в три раза уменьшается.

Как объяснить обратную зависимость давления от объёма с физической точки зрения? При постоянной температуре остаётся неизменной средняя кинетическая энергия молекул газа, то есть, попросту говоря, не меняется сила ударов молекул о стенки сосуда. При увеличении объёма концентрация молекул уменьшается, и соответственно уменьшается число ударов молекул в единицу времени на единицу площади стенки — давление газа падает. Наоборот, при уменьшении объёма концентрация молекул возрастает, их удары сыпятся чаще и давление газа увеличивается.